Câu hỏi:
2 năm trước
Phương trình \(\cos 3x = 2{m^2} - 3m + 1\). Xác định \(m\) để phương trình có nghiệm \(x \in \left( {0;\dfrac{\pi }{6}} \right]\).
Trả lời bởi giáo viên
Đáp án đúng: c
Bước 1:
Với \(x \in \left( {0;\dfrac{\pi }{6}} \right] \Rightarrow 3x \in \left( {0;\dfrac{\pi }{2}} \right]\).
Hàm số \(y = \cos x\) nghịch biến trên \(\left( {0;\dfrac{\pi }{2}} \right)\) nên ta có:
\(0 < 3x \le \dfrac{\pi}{2} \Leftrightarrow \cos \dfrac{\pi}{2} \le \cos 3x \le \cos 0 \Leftrightarrow 0 \le \cos 3x < 1\)
Bước 2:
Do đó phương trình \(\cos 3x = 2{m^2} - 3m + 1\) có nghiệm khi và chỉ khi:
\(0 \le 2{m^2} - 3m + 1 < 1\)
\(\Leftrightarrow \left\{ \matrix{
2{m^2} - 3m + 1 \ge 0 \hfill \cr
2{m^2} - 3m + 1 < 1 \hfill \cr} \right. \)
\(\Leftrightarrow \left\{ \matrix{
\left[ \matrix{
m \ge 1 \hfill \cr
m \le \dfrac{1}{2} \hfill \cr} \right. \hfill \cr
0 < m < \dfrac{3}{2} \hfill \cr} \right. \)
Kết hợp nghiệm:
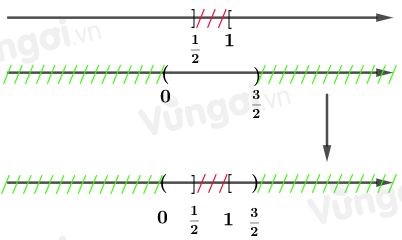
\(\Leftrightarrow m \in \left( {0;\dfrac{1}{2}} \right] \cup \left[ {1;\dfrac{3}{2}} \right)\)
Hướng dẫn giải:
Bước 1: Đánh giá $\cos 3x$
Sử dụng tính đồng biến, nghịch biến của hàm số \(y = \sin x\).
Bước 2: Tìm điều kiện của $m$
+) Hai vế của phương trình phải cùng thỏa mãn một điều kiện.
+) Sử dụng MTCT để giải các bất phương trình.
+) Kết hợp nghiệm của m trên trục số.
