Nghiệm của phương trình \(\sin x = \dfrac{1}{2}\) thỏa mãn $ - \dfrac{\pi }{2} \le x \le \dfrac{\pi }{2}$ là:
Trả lời bởi giáo viên
Bước 1:
Ta có: \(\sin x = \dfrac{1}{2} \Leftrightarrow \sin x = \sin \dfrac{\pi }{6}\)
Bước 2:
\( \Leftrightarrow \left[ \begin{array}{l}x = \dfrac{\pi }{6} + k2\pi \\x = \dfrac{{5\pi }}{6} + k2\pi \end{array} \right.\left( {k \in Z} \right)\)
Bước 3:
+) Xét $x = \dfrac{\pi }{6} + k2\pi$
Ta có $ - \dfrac{\pi }{2} \le x \le \dfrac{\pi }{2} \Leftrightarrow - \dfrac{\pi }{2} \le \dfrac{\pi }{6} + k2\pi \le \dfrac{\pi }{2} $
\(\begin{array}{l} - \dfrac{{2\pi }}{3} \le k2\pi \le \dfrac{\pi }{3} \Leftrightarrow - \dfrac{{2\pi }}{{3.2\pi }} \le k \le \dfrac{\pi }{{3.2\pi }}\\ \Leftrightarrow - \dfrac{1}{3} \le k \le \dfrac{1}{6}\end{array}\)
Mà \(k \in \mathbb{Z} \Rightarrow k = 0\). Thay vào x ta được: \(x = \dfrac{\pi }{6}\)
+) Xét \(x = \dfrac{{5\pi }}{6} + k2\pi \)
\(\begin{array}{l} - \dfrac{\pi }{2} \le x \le \dfrac{\pi }{2} \Leftrightarrow - \dfrac{\pi }{2} \le \dfrac{{5\pi }}{6} + k2\pi \le \dfrac{\pi }{2}\\ \Leftrightarrow - \dfrac{{4\pi }}{3} \le k2\pi \le - \dfrac{\pi }{3} \Leftrightarrow - \dfrac{{4\pi }}{{3.2\pi }} \le k \le - \dfrac{\pi }{{3.2\pi }}\\ \Leftrightarrow - \dfrac{2}{3} \le k \le - \dfrac{1}{6}\end{array}\)
Mà \(k \in \mathbb{Z}\) nên không có giá trị k thỏa mãn
Vậy phương trình ban đầu có nghiệm duy nhất là \(x = \dfrac{\pi }{6}\)
Hướng dẫn giải:
Bước 1: Đưa $\dfrac{1}{2}$ về dạng $\sin \alpha $
Sử dụng máy tính để tìm $\alpha $:
SHIFT => MODE => 4 : chuyển về chế độ Radian
SHIFT => SIN => (1/2) =>"="
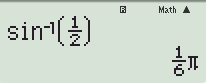
Bước 2: Giải phương trình lượng giác cơ bản \(\sin x = \sin \alpha \Leftrightarrow \left[ \begin{array}{l}x = \alpha + k2\pi \\x = \pi - \alpha + k2\pi \end{array} \right.\)
Bước 3: Xét từng họ nghiệm và thay vào $ - \dfrac{\pi }{2} \le x \le \dfrac{\pi }{2}$ để tìm k sau đó thay k ngược lại để tìm x.

