Công thức tính diện tích xung quanh hình nón có bán kính đáy \(r\) và độ dài đường sinh \(l\) là
Công thức tính diện tích xung quanh hình nón có bán kính đáy \(r\) và độ dài đường sinh \(l\) là: \({S_{xq}} = \pi rl\)
Một hình nón đỉnh \(S\) có bán kính đáy bằng \(2a\sqrt 3 \), góc ở đỉnh là \(120^\circ \). Thiết diện qua đỉnh của hình nón là một tam giác. Diện tích lớn nhất \({S_{\max }}\) của thiết diện đó là bao nhiêu?
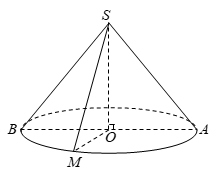
Giả sử \(O\) là tâm đáy và \(AB\) là một đường kính của đường tròn đáy hình nón.
Thiết diện qua đỉnh của hình nón là tam giác cân \(SAM\). Theo giả thiết hình nón có bán kính đáy \(R = OA = 2a\sqrt 3 \), \(\widehat {ASB} = 120^\circ \) nên \(\widehat {ASO} = 60^\circ \).
Xét tam giác \(SOA\) vông tại \(O\), ta có \(\sin 60^\circ = \dfrac{{OA}}{{SA}}\)\( \Rightarrow SA = \dfrac{{OA}}{{\sin 60^\circ }} = 4a\).
Diện tích thiết diện là \({S_{SAM}} = \dfrac{1}{2}SA.SM.\sin \widehat {ASM} = \dfrac{1}{2}.4a.4a.\sin \widehat {ASM} = 8{a^2}.\sin \widehat {ASM}\)
Do \(0 < \sin \widehat {ASM} \le 1\) nên \({S_{SAM}}\) lớn nhất khi và chỉ khi \(\sin \widehat {ASM} = 1\) hay khi tam giác \(ASM\) vuông cân đỉnh \(S\) (vì \(\widehat {ASB} = 120^\circ > 90^\circ \) nên tồn tại tam giác \(ASM\) thoả mãn).
Vậy diện tích thiết diện lớn nhất là \({S_{\max }} = 8{a^2}{\mkern 1mu} \)(đvdt).
Diện tích xung quanh hình nón có bán kính đáy \(r = 3cm\) và độ dài đường sinh \(4cm\) là:
Áp dụng công thức \({S_{xq}} = \pi rl\) ta được: \({S_{xq}} = \pi .3.4 = 12\pi \left( {c{m^2}} \right)\)
Một cái phễu có dạng hình nón có chiều cao $15(cm).$ Người ta đổ một lượng nước vào phễu sao cho chiều cao của lượng nước trong phễu bằng \(\dfrac{1}{3}\) chiều cao ban đầu của cái phễu (hình 1). Hỏi nếu bịt kín miệng phễu rồi lộn ngược phễu lên (hình 2) thì chiều cao của nước xấp xỉ bằng bao nhiêu (làm tròn đến hàng phần nghìn).
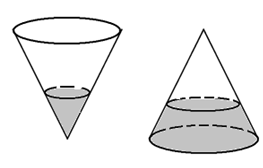
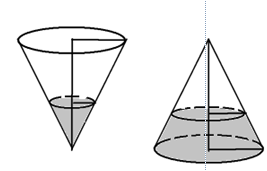
Gọi $r_1$ là bán kính đáy phễu, $r_2$ là bán kính đáy phần nước, $h_1$ và $h_2$ là chiều cao phễu và chiều cao cột nước ta có \(\dfrac{{{r_2}}}{{{r_1}}} = \dfrac{{{h_2}}}{{{h_1}}} = \dfrac{5}{{15}} = \dfrac{1}{3} \Rightarrow {r_2} = \dfrac{1}{3}{r_1}\)
Khi úp phễu xuống thì thể tích của phần nón không chứa nước là: \(\dfrac{1}{3}\pi r_1^2{h_1} - \dfrac{1}{3}\pi r_2^2{h_2} = 5\pi r_1^2 - \dfrac{5}{3}\pi {\left( {\dfrac{{{r_1}}}{3}} \right)^2} = \dfrac{{130}}{{27}}\pi r_1^2 = \dfrac{1}{3}\pi {r^2}h\) với $r, h$ là bán kính và chiều cao của hình nón không chứa nước \( \Rightarrow {r^2}h = \dfrac{{130}}{9}r_1^2\)
Ta có \(\dfrac{r}{{{r_1}}} = \dfrac{h}{{{h_1}}} \Rightarrow r = \dfrac{{{r_1}h}}{{15}} \Rightarrow \dfrac{{r_1^2{h^3}}}{{225}} = \dfrac{{130}}{9}r_1^2 \Leftrightarrow h = 14,812\,\left( {cm} \right)\)
Vậy chiều cao của nước sau khi úp phếu xuống là $15 – 14,812 = 0,188 (cm)$
Một cái phễu có dạng hình nón. Chiều cao của phễu là 20 cm. Người ta đổ một lượng nước vào phễu sao cho chiều cao của cột nước trong phễu bằng $10 cm$. Nếu bịt kín miệng phễu rồi lật ngược phễu lên thì chiều cao của cột nước trong phễu gần bằng với giá trị nào sau đây?

Gọi thể tích của phễu là $V,$ bán kính đáy phễu là $R,$ bán kính của cột nước có dạng khối nón trong H1 là $R_1$
Ta có: \(\dfrac{{10}}{{20}} = \dfrac{{{R_1}}}{R} = \dfrac{1}{2}\)
Gọi $V_1$ là thể tích của nước ta có:
\(\dfrac{{{V_1}}}{V} = \dfrac{{\dfrac{1}{3}\pi R_1^2.10}}{{\dfrac{1}{3}\pi{R^2}.20}} = \dfrac{1}{2}{\left( {\dfrac{{{R_1}}}{R}} \right)^2}= \dfrac{1}{8} \Rightarrow {V_1} = \dfrac{1}{8}V\)
Sau khi úp ngược phễu lên, thể tích của phần không có nước có dạng khối nón có thể tích là \({V_2} = V - {V_1} = \dfrac{7}{8}V\)
Gọi $h, R_2$ là chiều cao và bán kính đáy của khối nón không chứa nước ở H2 ta có
\(\dfrac{{{R_2}}}{R} = \dfrac{h}{{20}}\) và : \(\dfrac{{{V_2}}}{V}= \dfrac{{\dfrac{1}{3}\pi R_2^2h}}{{\dfrac{1}{3}\pi {R^2}.20}} = \dfrac{7}{8} \Rightarrow {\left( {\dfrac{{{R_2}}}{R}} \right)^2}.\dfrac{h}{{20}} =\dfrac{7}{8} \Leftrightarrow \dfrac{{{h^3}}}{{{{20}^3}}} = \dfrac{7}{8} \Rightarrow h = 10\sqrt[3]{7}\)
\( \Rightarrow \) Chiều cao của cột nước trong H2 là \(20 - 10\sqrt[3]{7}cm\) .
Công thức tính diện tích toàn phần hình nón có bán kính đáy \(r\), độ dài đường cao \(h\) và độ dài đường sinh \(l\) là:
Công thức tính diện tích toàn phần hình nón có bán kính đáy \(r\) và độ dài đường sinh \(l\) là: \({S_{tp}} = \pi rl + \pi {r^2}\)
Cho hình tứ diện $ABCD$ có $AD \bot (ABC)$, $ABC$ là tam giác vuông tại $B.$ Biết $BC = a,$ $AB = a\sqrt 3 $, $AD = 3a.$ Quay các tam giác $ABC$ và $ABD$ (bao gồm cả điểm bên trong 2 tam giác) xung quanh đường thẳng $AB$ ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng
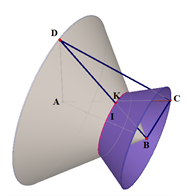
* Xét mặt phẳng (ABD):
Gọi C’ là điểm ở trong (ABD) sao cho: C’B vuông góc AB và C’B = BC = a.
Gọi $K = AC' \cap BD,\,\,IK \bot AB\,\,(I \in AB)$
Theo Ta – lét ta có:
$\dfrac{{IK}}{{BC'}} = \dfrac{{IA}}{{AB}} = 1 - \dfrac{{IB}}{{AB}} = 1 - \dfrac{{KI}}{{3BC'}} \Leftrightarrow \dfrac{4}{3}\dfrac{{KI}}{{BC'}} = 1 \Leftrightarrow \dfrac{{KI}}{{BC'}} = \dfrac{3}{4} \Rightarrow IK = \dfrac{3}{4}a$
Thể tích của phần chung là:
$V = \dfrac{1}{3}\pi I{K^2}.IA + \dfrac{1}{3}\pi I{K^2}.IB = \dfrac{1}{3}\pi I{K^2}.AB = \dfrac{1}{3}\pi .{\left( {\dfrac{{3a}}{4}} \right)^2}.a\sqrt 3 = \dfrac{{3\sqrt 3 \pi {a^3}}}{{16}}$
Cho hình nón có các kích thước \(r = 1cm;l = 2cm\) với \(r,l\) lần lượt là bán kính đáy và độ dài đường sinh hình nón. Diện tích toàn phần hình nón là:
Áp dụng công thức \({S_{tp}} = \pi rl + \pi {r^2}\) ta được: \({S_{tp}} = \pi rl + \pi {r^2} = \pi .1.2 + \pi {.1^2} = 3\pi \left( {c{m^2}} \right)\)
Cho hình nón có các kích thước \(r = 1;h = 2\) với \(r,h\) lần lượt là bán kính đáy và độ dài đường cao hình nón. Diện tích toàn phần hình nón là:
Ta có: \({l^2} = {r^2} + {h^2} \Rightarrow l = \sqrt {{r^2} + {h^2}} = \sqrt {{1^2} + {2^2}} = \sqrt 5 \)
Do đó \({S_{tp}} = \pi rl + \pi {r^2} = \pi .1.\sqrt 5 + \pi {.1^2} = \left( {1 + \sqrt 5 } \right)\pi \)
Công thức tính thể tích khối nón có bán kính đáy \(r\), độ dài đường sinh \(l\) và chiều cao \(h\) là:
Công thức tính thể tích khối nón: \(V = \dfrac{1}{3}\pi {r^2}h\)
Cho hình nón ${N_1}$ có chiều cao bằng $40cm$. Người ta cắt hình nón ${N_1}$ bằng một mặt phẳng song song với đáy của có để được một hình nón nhỏ ${N_2}$ có thể tích bằng $\dfrac{1}{8}$thể tích ${N_1}$. Tính chiều cao h của hình nón ${N_2}$?
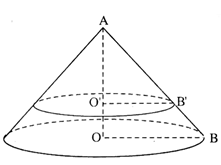
(Quan sát kí hiệu trên hình vẽ)
Áp dụng định lí Ta lét ta có:
$\dfrac{{O'B'}}{{OB}} = \dfrac{{O'A}}{{OA}} = \dfrac{{h'}}{h} = \dfrac{{h'}}{{40}}$ $(OA = h, O’A = h’< 40cm)$
Tỉ số thể tích giữa 2 khối nón:
$\begin{array}{l}\dfrac{{V'}}{V} = \dfrac{{\dfrac{1}{3}\pi .O'B{'^2}.O'A}}{{\dfrac{1}{3}\pi .O{B^2}.OA}} = \dfrac{{O'B{'^2}.O'A}}{{O{B^2}.OA}} = {\left( {\dfrac{{O'B'}}{{OB}}} \right)^2}.\dfrac{{O'A}}{{OA}} = {\left( {\dfrac{{h'}}{{40}}} \right)^2}.\dfrac{{h'}}{{40}} = \dfrac{1}{8}\\ \Rightarrow h{'^3} = \dfrac{{{{40}^3}}}{8} = {20^3} \Rightarrow h' = 20\,\,(cm)\end{array}$
Vậy chiều cao $h$ của hình nón ${N_2}$ là: $20cm.$
Thể tích khối nón có bán kính đáy \(r = 2cm\) và \(h = 3cm\) là:
Áp dụng công thức tính thể tích khối nón \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {.2^2}.3 = 4\pi c{m^3}\)
Công thức tính thể tích khối nón biết diện tích đáy \({S_d}\) và đường sinh \(l\) là:
Ta có: \({l^2} = {r^2} + {h^2} \Rightarrow h = \sqrt {{l^2} - {r^2}} \Rightarrow V = \dfrac{1}{3}{S_d}.h = \dfrac{1}{3}{S_d}.\sqrt {{l^2} - {r^2}} \)
Cho tam giác $ABO$ vuông tại $O$, có góc \(\widehat {BAO} = {30^0},AB = a\) . Quay tam giác $ABO$ quanh trục $AO$ ta được một hình nón có diện tích xung quanh bằng:
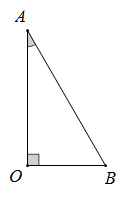
Hình nón thu được có đường sinh $l = AB = a$; bán kính đáy
$r = OB = AB.\sin 30^\circ = \dfrac{a}{2}$ và diện tích xung quanh là
${S_{xq}} = \pi rl = \dfrac{{\pi {a^2}}}{2}$
Một hình nón tròn xoay có đường sinh bằng đường kính đáy. Diện tích đáy của hình nón bằng $9\pi $. Khi đó chiều cao $h$ của hình nón bằng:
$r = \sqrt {\dfrac{{9\pi }}{\pi }} = 3 \Rightarrow l = 2r = 6;h = \sqrt {{l^2} - {r^2}} = 3\sqrt 3 $
Hình nón có thiết diện qua trục là tam giác đều cạnh \(a = 3\). Tính độ dài đường cao của hình nón.
Độ dài đường cao của hình nón cũng chính là chiều cao của tam giác đều \( \Rightarrow h = \dfrac{{a\sqrt 3 }}{2} = \dfrac{{3\sqrt 3 }}{2}\)
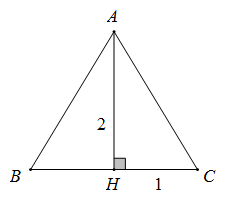
Một hình nón có bán kính đáy bằng $1$, chiều cao nón bằng $2$. Khi đó góc ở đỉnh của nón là $2\varphi $ thỏa mãn
Giả sử thiết diện qua trục của hình nón đã cho là $\Delta ABC$ cân tại $A$ với $A$ là đỉnh nón, $BC$ là đường kính đáy của nón.
Gọi $H$ là tâm đáy nón $ \Rightarrow H$ là trung điểm $BC,AH \bot BC$
Ta có $HB = HC = 1,AH = 2$ . Ta có
$\begin{array}{l}2\varphi = \angle BAC \Rightarrow \varphi = \angle HAC\\AC = \sqrt {A{H^2} + H{C^2}} = \sqrt 5 \\\cos \varphi = \dfrac{{AH}}{{AC}} = \dfrac{2}{{\sqrt 5 }} = \dfrac{{2\sqrt 5 }}{5}\end{array}$
Người ta đặt được vào một hình nón hai khối cầu có bán kính lần lượt là $a$ và $2a$ sao cho các khối cầu đều tiếp xúc với mặt xung quanh của hình nón, hai khối cầu tiếp xúc với nhau và khối cầu lớn tiếp xúc với đáy của hình nón. Bán kính đáy của hình nón đã cho là:
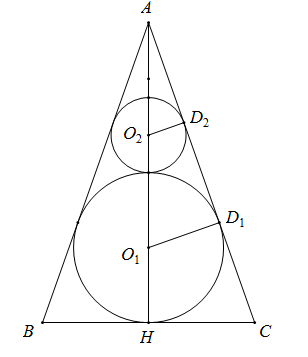
Giả sử thiết diện qua trục của hình nón là $\Delta ABC$ với $A$ là đỉnh nón, $BC$ là đường kính đáy nón.
Gọi $H$ là tâm đường tròn đáy của hình nón, ${O_1},{O_2}$ lần lượt là tâm của mặt cầu lớn và nhỏ, ${D_1},{D_2}$ lần lượt là tiếp điểm của $AC$ với $\left( {{O_1}} \right)$ và $\left( {{O_2}} \right)$.
Vì ${O_1}{D_1}//{O_2}{D_2}$ (cùng vuông góc với $AC$) nên theo hệ thức Ta – let ta có:
\( \Rightarrow \dfrac{{A{O_2}}}{{A{O_1}}} = \dfrac{{{O_2}{D_2}}}{{{O_1}{D_1}}} = \dfrac{a}{{2a}} = \dfrac{1}{2} \)
\(\Rightarrow {O_2}\) là trung điểm của \(A{O_1}\)\( \Rightarrow A{O_1} = 2{O_1}{O_2} = 2\left( {a + 2a} \right) = 6a\)
\( \Rightarrow AH = A{O_1} + {O_1}H = 6a + 2a = 8a\)
Xét tam giác vuông \(A{O_1}{D_1}\) có: \(A{D_1} = \sqrt {A{O_1}^2 - {O_1}{D_1}^2} = \sqrt {36{a^2} - 4{a^2}} = 4\sqrt 2 a\)
Dễ thấy:
$\Delta A{O_1}{D_1} \backsim \Delta ACH\,\,\left( {g.g} \right)$$ \Rightarrow \dfrac{{HC}}{{{O_1}{D_1}}} = \dfrac{{AH}}{{A{D_1}}}$$ \Rightarrow HC = \dfrac{{{O_1}{D_1}.AH}}{{A{D_1}}} = \dfrac{{2a.8a}}{{4\sqrt 2 a}} = 2\sqrt 2 a = r$
Cho hình nón có diện tích xung quanh bằng \(3\pi {a^2}\) và bán kính đáy bằng \(a\). Tính độ dài đường sinh \(l\) của hình nón đã cho.
Ta có: \({S_{xq}} = \pi rl = 3\pi {a^2} = \pi al \Rightarrow l = 3a\)
Cho mặt cầu tâm \(O\) bán kính \(R\). Xét mặt phẳng \(\left( P \right)\) thay đổi cắt mặt cầu theo giao tuyến là đường tròn \(\left( C \right)\). Hình nón \(N\) có đỉnh \(S\) nằm trên mặt cầu, có đáy là đường tròn \(\left( C \right)\) và có chiều cao \(h\left( {h > R} \right)\). Tìm \(h\) để thể tích khối nón được tạo nên bởi \(\left( N \right)\) có giá trị lớn nhất.
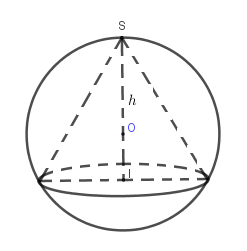
Ta có: Gọi bán kính $\left( C \right)$ với tâm là $I$ là $r$ thì dễ có $S$ phải thuộc $OI$ và :
$\begin{array}{l}OI = \sqrt {{R^2} - {r^2}} \to h = \sqrt {{R^2} - {r^2}} + R\\V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi {r^2}(\sqrt {{R^2} - {r^2}} + R)\end{array}$
Tới đây ta sẽ khảo sát hàm số:
\(\begin{array}{l}
f\left( r \right) = {r^2}\left( {\sqrt {{R^2} - {r^2}} + R} \right)\\
= {r^2}\sqrt {{R^2} - {r^2}} + {r^2}R\\
\Rightarrow f'\left( r \right) = \left( {{r^2}\sqrt {{R^2} - {r^2}} + {r^2}R} \right)'\\
= \left( {{r^2}\sqrt {{R^2} - {r^2}} } \right)' + \left( {{r^2}R} \right)'\\
= \left( {{r^2}} \right)'\sqrt {{R^2} - {r^2}} + {r^2}\left( {\sqrt {{R^2} - {r^2}} } \right)' + 2rR\\
= 2r\sqrt {{R^2} - {r^2}} + {r^2}.\frac{{ - 2r}}{{2\sqrt {{R^2} - {r^2}} }} + 2rR\\
= 2r\sqrt {{R^2} - {r^2}} - \frac{{{r^3}}}{{\sqrt {{R^2} - {r^2}} }} + 2rR\\
= r\left( {2\sqrt {{R^2} - {r^2}} - \frac{{{r^2}}}{{\sqrt {{R^2} - {r^2}} }} + 2R} \right)
\end{array}\)
$f'(r) = 0 \Leftrightarrow 2\sqrt {{R^2} - {r^2}} + 2{\rm{R}} - \dfrac{{{r^2}}}{{\sqrt {{R^2} - {r^2}} }} = 0 \Leftrightarrow 2({R^2} - {r^2}) - {r^2} + 2{\rm{R}}\sqrt {{R^2} - {r^2}} = 0$
$ \Leftrightarrow {(2{{\rm{R}}^2} - 3{{\rm{r}}^2})^2} = {(2{\rm{R}}\sqrt {{R^2} - {r^2}} )^2}$
$\Leftrightarrow {r^2} = \dfrac{8}{9}{R^2} \to h = \dfrac{{4{\rm{R}}}}{3}.$

