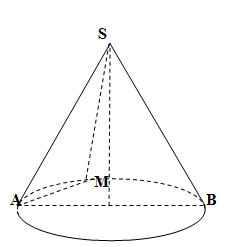
Cho hình nón đỉnh $S$, tâm đáy là $O$, góc ở đỉnh là ${135^0}$. Trên đường tròn đáy lấy điểm $A$ cố định và điểm $M$ di động. Tìm số vị trí $M$ để diện tích $SAM$ đạt giá trị lớn nhất
Ta có:
\(\begin{array}{l}{S_{SAM}} = \dfrac{1}{2}SA.SM\sin \widehat {ASM}\\ = \dfrac{1}{2}S{A^2}\sin \widehat {ASM} \le \dfrac{1}{2}S{A^2}\\ \Rightarrow \max {S_{SAM}} = \dfrac{1}{2}S{A^2}\end{array}\)
Dấu “=” xảy ra khi \(\sin \widehat {ASM} = 1 \Leftrightarrow \widehat {ASM} = {90^0}\).
Có $2$ điểm $M$ như vậy (hai điểm đối xứng với nhau qua $AB$).
Một que kem ốc quế gồm hai phần: phần kem có dạng hình cầu, phần ốc quế có dạng hình nón. Giả sử hình cầu và hình nón có bán kính bằng nhau; biết rằng nếu kem tan chảy hết thì sẽ làm đầy phần ốc quế. Biết thể tích phần kem sau khi tan chảy chỉ bằng $75\% $ thể tích kem đóng băng ban đầu. Gọi $h$ và $r$ lần lượt là chiều cao và bán kính của phần ốc quế. Tính tỉ số \(\dfrac{h}{r}\).
Theo đầu bài ta có bán kính của khối cầu và khối nón đều bằng $r$.
Từ dữ kiện đầu bài ta suy ra : \({V_{non}} = \dfrac{3}{4}.{V_{cau}} \Leftrightarrow \dfrac{1}{3}\pi {r^2}h = \dfrac{3}{4}.\dfrac{4}{3}\pi {r^3} \Leftrightarrow \dfrac{h}{r} = 3\)
Cho hình chóp \(S.ABCD\) có \(SA\) vuông góc với mặt phẳng \(\left( {ABCD} \right)\); tứ giác \(ABCD\) là hình thang vuông với cạnh đáy \(AD,BC\); \(AD = 3BC = 3a,\,\,AB = a,SA = a\sqrt 3 \). Điểm \(I\) thỏa mãn \(\overrightarrow {AD} = 3\overrightarrow {AI} \); \(M\) là trung điểm \(SD\), \(H\) là giao điểm của \(AM\) và \(SI\). Gọi \(E\), \(F\) lần lượt là hình chiếu của \(A\) lên \(SB\), \(SC.\) Tính thể tích \(V\) của khối nón có đáy là đường tròn ngoại tiếp tam giác \(EFH\) và đỉnh thuộc mặt phẳng\(\left( {ABCD} \right)\).
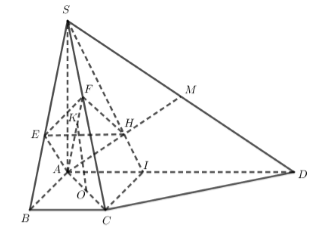
Xét tam giác \(SAD\) vuông tại \(A\) có \(SA = a\sqrt 3 ,AD = 3a \Rightarrow \widehat {SDA} = {30^0}\) \( \Rightarrow \widehat {MAI} = {30^0}\).
Lại có tam giác \(SAI\) vuông tại \(A\) có \(SA = a\sqrt 3 ,AI = a \Rightarrow \widehat {SIA} = {60^0}\) nên tam giác \(AHI\) có \(\widehat H = {90^0}\) hay \(AH \bot SI\)
Mà \(AH \bot IC\) do \(IC//BA \bot \left( {SAD} \right)\) nên \(AH \bot \left( {SIC} \right)\) \( \Rightarrow AH \bot SC\).
Ngoài ra, \(AE \bot SB,AE \bot BC\left( {BC \bot \left( {SAB} \right)} \right) \Rightarrow AE \bot \left( {SBC} \right) \Rightarrow AE \bot SC\).
Mà \(AF \bot SC\) nên \(SC \bot \left( {AEFH} \right)\) và \(AEFH\) là tứ giác có \(\widehat E = \widehat H = {90^0}\) nên nội tiếp đường tròn tâm \(K\) là trung điểm \(AF\) đường kính \(AF\).
Gọi \(O\) là trung điểm \(AC\) thì \(OK//SC\), mà \(SC \bot \left( {AEFH} \right)\) nên \(OK \bot \left( {AEFH} \right)\) hay \(O\) chính là đỉnh hình nón và đường tròn đáy là đường tròn đường kính \(AF\).
Ta tính \(AF,OK\).
Xét tam giác \(SAC\) vuông tại \(A\) đường cao \(AF\) nên \(AF = \dfrac{{SA.AC}}{{SC}} = \dfrac{{SA.AC}}{{\sqrt {S{A^2} + A{C^2}} }} = \dfrac{{a\sqrt 6 }}{{\sqrt 5 }}\).; \(OK = \dfrac{1}{2}CF = \dfrac{1}{2}.\dfrac{{C{A^2}}}{{CS}} = \dfrac{a}{{\sqrt 5 }}\).
Vậy thể tích \(V = \dfrac{1}{3}\pi {r^2}h = \dfrac{1}{3}\pi .\dfrac{a}{{\sqrt 5 }}.{\left( {\dfrac{1}{2}.\dfrac{{a\sqrt 6 }}{{\sqrt 5 }}} \right)^2} = \dfrac{{\pi {a^3}}}{{10\sqrt 5 }}\).
Cho hình vuông \(ABCD\) cạnh bằng \(2\). Gọi \(M\) là trung điểm \(AB\). Cho tứ giác \(AMCD\) và các điểm trong của nó quay quanh trục \(AD\) ta được một khối tròn xoay. Tính thể tích khối tròn xoay đó.
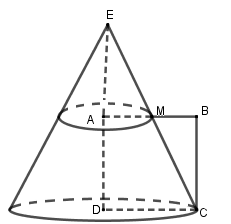
Kéo dài \(CM\) cắt \(DA\) tại \(E\). Quay hình thang vuông \(AMCD\) quanh trục \(AD\) ta được hình nón cụt như hình vẽ.
Quay tam giác \(EDC\) quanh trục \(ED\) ta được hình nón.
Dễ thấy \({V_{nc}} = {V_1} - {V_2}\), ở đó \({V_1}\) là thể tích khối nón đỉnh \(E\), bán kính đáy \(DC = 2\) và \({V_2}\) là thể tích khối nón đỉnh \(E\), bán kính đáy \(AM = 1\).
Có \(\dfrac{{EA}}{{ED}} = \dfrac{{AM}}{{DC}} = \dfrac{1}{2} \Rightarrow EA = AD = 2 \Rightarrow ED = 4\)
\( \Rightarrow {V_1} = \dfrac{1}{3}\pi D{C^2}.ED = \dfrac{1}{3}\pi {.2^2}.4 = \dfrac{{16\pi }}{3}\) ;
\({V_2} = \dfrac{1}{3}\pi A{M^2}EA = \dfrac{1}{3}\pi {.1^2}.2 = \dfrac{{2\pi }}{3}\).
Vậy \(V = {V_1} - {V_2} = \dfrac{{16\pi }}{3} - \dfrac{{2\pi }}{3} = \dfrac{{14\pi }}{3}\).
Một hình nón có thiết diện qua trục là một tam giác vuông cân có cạnh góc vuông bằng \(a.\) Diện tích xung quanh của hình nón bằng:
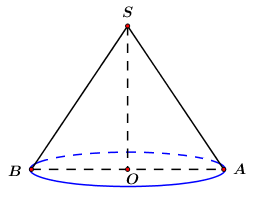
Thiết diện qua trục của hình nón là \(\Delta SAB\) vuông cân tại \(S\) và có \(SA = SB = a.\)
\( \Rightarrow l = SA = a.\)
Ta có:\(\Delta SAB\) vuông cân tại \(S\) \( \Rightarrow AB = SA\sqrt 2 = a\sqrt 2 \)
\( \Rightarrow r = OA = \dfrac{1}{2}AB = \dfrac{{a\sqrt 2 }}{2}.\)
\( \Rightarrow \) Diện tích xung quanh của hình nón đã cho là:\({S_{xq}} = \pi rl = \pi .\dfrac{{a\sqrt 2 }}{2}.a = \dfrac{{\pi {a^2}\sqrt 2 }}{2}.\)
Cho hình nón có góc ở đỉnh bằng \({120^0}\) và đường cao bằng \(2.\) Tính diện tích xung quanh của hình nón đã cho.
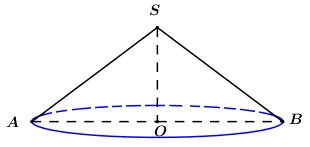
Gọi \(S\) là đỉnh hình nón, \(AB\) là 1 đường kính của hình nón và \(O\) là tâm đường tròn đáy của hình nón.
Khi đó ta có \(\angle ASB = {120^0}\) và \(h = SO = 2\).
Ta có: \(\Delta SAB\) cân tại \(S\) suy ra \(SO\) là phân giác của \(\angle ASB\) \( \Rightarrow \angle ASO = \dfrac{1}{2}\angle ASB = {60^0}\).
Xét tam giác vuông \(SOA\) có: \(r = OA = SO.\tan {60^0} = 2\sqrt 3 \), \(l = SA = \dfrac{{SO}}{{\cos {{60}^0}}} = 4\).
Vậy diện tích xung quanh của hình nón là: \({S_{xq}} = \pi rl = \pi .2\sqrt 3 .4 = 8\sqrt 3 \pi \).
Cho tam giác ABC đều, có diện tích bằng \({s_1}\) và \(AH\) là đường cao. Quay tam giác ABC quanh đường thẳng \(AH\) ta thu được hình nón có diện tích xung quanh bằng \({s_2}\). Tính \(\dfrac{{{s_1}}}{{{s_2}}}\).
Giả sử tam giác ABC đều cạnh a \( \Rightarrow {s_1} = {S_{ABC}} = \dfrac{{{a^2}\sqrt 3 }}{4}\)
Quay tam giác ABC quanh đường thẳng \(AH\) ta thu được hình nón có đường sinh \(l = AB = a\), bán kính đáy \(r = \dfrac{{BC}}{2} = \dfrac{a}{2}\), do đó diện tích xung quanh của hình nón bằng: \({s_2} = \pi rl = \pi .\dfrac{a}{2}.a = \dfrac{{\pi {a^2}}}{2}\).
Vậy \(\dfrac{{{s_1}}}{{{s_2}}} = \dfrac{{\dfrac{{{a^2}\sqrt 3 }}{4}}}{{\dfrac{{\pi {a^2}}}{2}}} = \dfrac{{\sqrt 3 }}{{2\pi }}\).
Cho hình nón đỉnh \(S\) có bán kính đáy \(R = 2\). Biết diện tích xung quanh của hình nón là \(2\sqrt 5 \pi \). Tính thể tích khối nón.
Ta có : \({S_{xq}} = \pi Rl \Rightarrow 2\sqrt 5 \pi = \pi .2l \Leftrightarrow l = \sqrt 5 \).
Lại có \({l^2} = {R^2} + {h^2} \Leftrightarrow {\left( {\sqrt 5 } \right)^2} = {2^2} + {h^2}\)\( \Leftrightarrow {h^2} = 1 \Leftrightarrow h = 1\).
Vậy thể tích khối nón là : \(V = \dfrac{1}{3}\pi {R^2}h = \dfrac{1}{3}\pi {.2^2}.1 = \dfrac{4}{3}\pi \).
Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có đáy là hình thoi cạnh \(a\) và góc \(\widehat {BAD} = q\). Mặt chéo \(AC{C^\prime }{A^\prime }\) nằm trong mặt phẳng vuông góc với đáy, đồng thời \(AC{C^\prime }{A^\prime }\) ' là hình thoi có góc \(\widehat {{A^\prime }AC} = {60^0 }\).
Tính tan góc giữa hai mặt phẳng \(\left( {BC{C^\prime }{B^\prime }} \right)\) và \((ABCD)\).
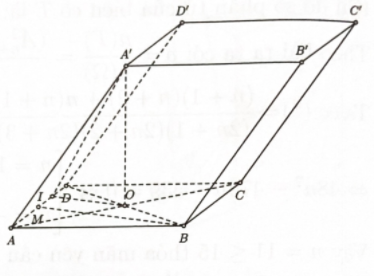
Bước 1: Xác định góc giữa hai mặt phẳng \(\left( {BC{C^\prime }{B^\prime }} \right)\) và \((ABCD)\)
Gọi \(M\) là trung điểm $A D$
\( \Rightarrow BM \bot AD({\mathop{\rm tam}\nolimits} \) giác $A B D$ I$ là trung điểm $M D$
\( \Rightarrow OI \bot AD \Rightarrow \) góc giữa hai mặt phẳng \(\left( {BC{C^\prime }{B^\prime }} \right)\) và \((ABCD)\) bằng \(\widehat {{A^\prime }IO}\).
Bước 2: Tính \(\tan \widehat {{A^\prime }IO}\)
Ta có \(AC = 2AO = 2 \cdot \dfrac{{a\sqrt 3 }}{2} = a\sqrt 3 \).
Xét tam giác \(A{A^\prime }O\) vuông tại \(O\) có: \({A^\prime }O = AO \cdot \tan {60^0 } = \dfrac{{a\sqrt 3 }}{2} \cdot \sqrt 3 = \dfrac{{3a}}{2}\).
Xét \(\Delta BMD\) có: \(OI = \dfrac{1}{2}BM = \dfrac{{a\sqrt 3 }}{4}\).
Xét tam giác \({A^\prime }IO\) vuông tại \(O\) có: \(\tan \widehat {{A^\prime }IO} = \dfrac{{{A^\prime }O}}{{OI}} = 2\sqrt 3 \)
Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có đáy là hình thoi cạnh \(a\) và góc \(\widehat {BAD} = q\). Mặt chéo \(AC{C^\prime }{A^\prime }\) nằm trong mặt phẳng vuông góc với đáy, đồng thời \(AC{C^\prime }{A^\prime }\) ' là hình thoi có góc \(\widehat {{A^\prime }AC} = {60^0 }\).
Tính thể tích khối tứ diện \(AC{B^\prime }{D^\prime }\).
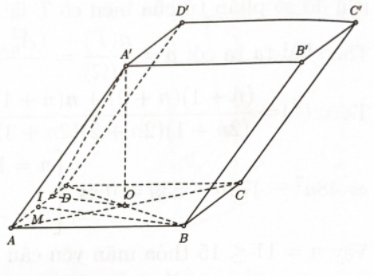
Bước 1: Tính \({S_{ABCD}};A'O\)
Ta có \({S_{ABCD}} = 2{S_{ABD}}\)\( = 2 \cdot \dfrac{1}{2}AB \cdot AD \cdot \sin {60^0 } = \dfrac{{{a^2}\sqrt 3 }}{2};\)\({A^\prime }O = \dfrac{{3a}}{2}\).
Bước 2: Tính \({V_{AC{B^\prime }{D^\prime }}} = \dfrac{1}{3}{V_{ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }}}\)
=> \({V_{AC{B^\prime }{D^\prime }}} = \dfrac{1}{3}{V_{ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }}}\)\( = \dfrac{1}{3} \cdot {A^\prime }O \cdot {S_{ABCD}}\)\( = \dfrac{1}{3} \cdot \dfrac{{3a}}{2} \cdot \dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 3 }}{4}\)
Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có đáy là hình thoi cạnh \(a\) và góc \(\widehat {BAD} = q\). Mặt chéo \(AC{C^\prime }{A^\prime }\) nằm trong mặt phẳng vuông góc với đáy, đồng thời \(AC{C^\prime }{A^\prime }\) ' là hình thoi có góc \(\widehat {{A^\prime }AC} = {60^0 }\).
Tính diện toàn phần của hình nón có đáy là đường tròn nội tiếp \(\Delta ABD\) và chiều cao bằng chiều cao của lăng trụ.
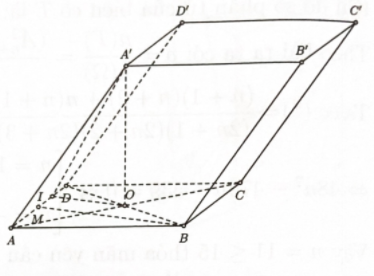
Bước 1: Tính bán kính đường tròn đáy của hình nón.
Vì \(\Delta ABD\) đều nên tâm đường tròn nội tiếp tam giác trùng với trọng tâm của tam giác
\( \Rightarrow \) Bán kính đường tròn đáy của hình nón là: \(r = \dfrac{{BM}}{3} = \dfrac{{a\sqrt 3 }}{6}\).
Bước 2: Tính diện tích xung quanh của hình nón \({S_{xq}} = \pi rl + \pi {r^2}\)
Vì chiều cao của hình nón bằng chiều cao của lăng trụ nên ta có độ dài đường sinh là
\(l = \sqrt {{A^\prime }{O^2} - {r^2}} \)\( = \sqrt {{{\left( {\dfrac{{3a}}{2}} \right)}^2} - {{\left( {\dfrac{{a\sqrt 3 }}{6}} \right)}^2}} = \dfrac{{a\sqrt {159} }}{6}\)
Vậy diện tích xung quanh của hình nón là: \({S_{xq}} = \pi rl + \pi {r^2}\)\( = \dfrac{{\pi {a^2}(\sqrt {53} + 1)}}{{12}}\).

