Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có đáy là hình thoi cạnh \(a\) và góc \(\widehat {BAD} = q\). Mặt chéo \(AC{C^\prime }{A^\prime }\) nằm trong mặt phẳng vuông góc với đáy, đồng thời \(AC{C^\prime }{A^\prime }\) ' là hình thoi có góc \(\widehat {{A^\prime }AC} = {60^0 }\).
Tính tan góc giữa hai mặt phẳng \(\left( {BC{C^\prime }{B^\prime }} \right)\) và \((ABCD)\).
Trả lời bởi giáo viên
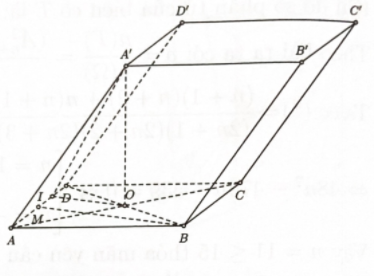
Bước 1: Xác định góc giữa hai mặt phẳng \(\left( {BC{C^\prime }{B^\prime }} \right)\) và \((ABCD)\)
Gọi \(M\) là trung điểm $A D$
\( \Rightarrow BM \bot AD({\mathop{\rm tam}\nolimits} \) giác $A B D$ I$ là trung điểm $M D$
\( \Rightarrow OI \bot AD \Rightarrow \) góc giữa hai mặt phẳng \(\left( {BC{C^\prime }{B^\prime }} \right)\) và \((ABCD)\) bằng \(\widehat {{A^\prime }IO}\).
Bước 2: Tính \(\tan \widehat {{A^\prime }IO}\)
Ta có \(AC = 2AO = 2 \cdot \dfrac{{a\sqrt 3 }}{2} = a\sqrt 3 \).
Xét tam giác \(A{A^\prime }O\) vuông tại \(O\) có: \({A^\prime }O = AO \cdot \tan {60^0 } = \dfrac{{a\sqrt 3 }}{2} \cdot \sqrt 3 = \dfrac{{3a}}{2}\).
Xét \(\Delta BMD\) có: \(OI = \dfrac{1}{2}BM = \dfrac{{a\sqrt 3 }}{4}\).
Xét tam giác \({A^\prime }IO\) vuông tại \(O\) có: \(\tan \widehat {{A^\prime }IO} = \dfrac{{{A^\prime }O}}{{OI}} = 2\sqrt 3 \)
Hướng dẫn giải:
Bước 1: Xác định góc giữa hai mặt phẳng \(\left( {BC{C^\prime }{B^\prime }} \right)\) và \((ABCD)\)
Bước 2: Tính \(\tan \widehat {{A^\prime }IO}\)