Câu hỏi:
2 năm trước
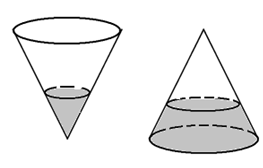
Một cái phễu có dạng hình nón. Chiều cao của phễu là 20 cm. Người ta đổ một lượng nước vào phễu sao cho chiều cao của cột nước trong phễu bằng $10 cm$. Nếu bịt kín miệng phễu rồi lật ngược phễu lên thì chiều cao của cột nước trong phễu gần bằng với giá trị nào sau đây?
Trả lời bởi giáo viên
Đáp án đúng: c
Gọi thể tích của phễu là $V,$ bán kính đáy phễu là $R,$ bán kính của cột nước có dạng khối nón trong H1 là $R_1$
Ta có: \(\dfrac{{10}}{{20}} = \dfrac{{{R_1}}}{R} = \dfrac{1}{2}\)
Gọi $V_1$ là thể tích của nước ta có:
\(\dfrac{{{V_1}}}{V} = \dfrac{{\dfrac{1}{3}\pi R_1^2.10}}{{\dfrac{1}{3}\pi{R^2}.20}} = \dfrac{1}{2}{\left( {\dfrac{{{R_1}}}{R}} \right)^2}= \dfrac{1}{8} \Rightarrow {V_1} = \dfrac{1}{8}V\)
Sau khi úp ngược phễu lên, thể tích của phần không có nước có dạng khối nón có thể tích là \({V_2} = V - {V_1} = \dfrac{7}{8}V\)
Gọi $h, R_2$ là chiều cao và bán kính đáy của khối nón không chứa nước ở H2 ta có
\(\dfrac{{{R_2}}}{R} = \dfrac{h}{{20}}\) và : \(\dfrac{{{V_2}}}{V}= \dfrac{{\dfrac{1}{3}\pi R_2^2h}}{{\dfrac{1}{3}\pi {R^2}.20}} = \dfrac{7}{8} \Rightarrow {\left( {\dfrac{{{R_2}}}{R}} \right)^2}.\dfrac{h}{{20}} =\dfrac{7}{8} \Leftrightarrow \dfrac{{{h^3}}}{{{{20}^3}}} = \dfrac{7}{8} \Rightarrow h = 10\sqrt[3]{7}\)
\( \Rightarrow \) Chiều cao của cột nước trong H2 là \(20 - 10\sqrt[3]{7}cm\) .
Hướng dẫn giải:
Sử dụng công thức tính thể tích khối nón \({V_n} = \dfrac{1}{3}\pi {R^2}h\) trong đó $R, h$ lần lượt là bán kính đáy và chiều cao của hình nón.
