Câu hỏi:
2 năm trước
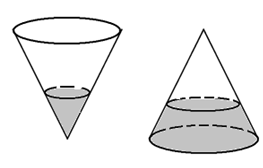
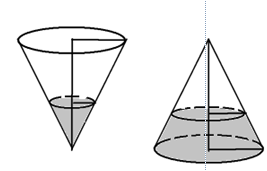
Một cái phễu có dạng hình nón có chiều cao $15(cm).$ Người ta đổ một lượng nước vào phễu sao cho chiều cao của lượng nước trong phễu bằng \(\dfrac{1}{3}\) chiều cao ban đầu của cái phễu (hình 1). Hỏi nếu bịt kín miệng phễu rồi lộn ngược phễu lên (hình 2) thì chiều cao của nước xấp xỉ bằng bao nhiêu (làm tròn đến hàng phần nghìn).
Trả lời bởi giáo viên
Đáp án đúng: d
Gọi $r_1$ là bán kính đáy phễu, $r_2$ là bán kính đáy phần nước, $h_1$ và $h_2$ là chiều cao phễu và chiều cao cột nước ta có \(\dfrac{{{r_2}}}{{{r_1}}} = \dfrac{{{h_2}}}{{{h_1}}} = \dfrac{5}{{15}} = \dfrac{1}{3} \Rightarrow {r_2} = \dfrac{1}{3}{r_1}\)
Khi úp phễu xuống thì thể tích của phần nón không chứa nước là: \(\dfrac{1}{3}\pi r_1^2{h_1} - \dfrac{1}{3}\pi r_2^2{h_2} = 5\pi r_1^2 - \dfrac{5}{3}\pi {\left( {\dfrac{{{r_1}}}{3}} \right)^2} = \dfrac{{130}}{{27}}\pi r_1^2 = \dfrac{1}{3}\pi {r^2}h\) với $r, h$ là bán kính và chiều cao của hình nón không chứa nước \( \Rightarrow {r^2}h = \dfrac{{130}}{9}r_1^2\)
Ta có \(\dfrac{r}{{{r_1}}} = \dfrac{h}{{{h_1}}} \Rightarrow r = \dfrac{{{r_1}h}}{{15}} \Rightarrow \dfrac{{r_1^2{h^3}}}{{225}} = \dfrac{{130}}{9}r_1^2 \Leftrightarrow h = 14,812\,\left( {cm} \right)\)
Vậy chiều cao của nước sau khi úp phếu xuống là $15 – 14,812 = 0,188 (cm)$
Hướng dẫn giải:
+) Tính thể tích của phần không chứa nước sau khi úp phễu xuống.
+) Tính chiều cao của nón sau khi úp phễu xuống.
+) Sử dụng công thức tính thể tích khối nón \(V = \dfrac{1}{3}\pi {r^2}h\) và sử dụng định lí Ta-let.
