Câu hỏi:
2 năm trước
Một hình nón đỉnh \(S\) có bán kính đáy bằng \(2a\sqrt 3 \), góc ở đỉnh là \(120^\circ \). Thiết diện qua đỉnh của hình nón là một tam giác. Diện tích lớn nhất \({S_{\max }}\) của thiết diện đó là bao nhiêu?
Trả lời bởi giáo viên
Đáp án đúng: a
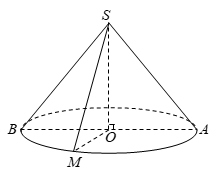
Giả sử \(O\) là tâm đáy và \(AB\) là một đường kính của đường tròn đáy hình nón.
Thiết diện qua đỉnh của hình nón là tam giác cân \(SAM\). Theo giả thiết hình nón có bán kính đáy \(R = OA = 2a\sqrt 3 \), \(\widehat {ASB} = 120^\circ \) nên \(\widehat {ASO} = 60^\circ \).
Xét tam giác \(SOA\) vông tại \(O\), ta có \(\sin 60^\circ = \dfrac{{OA}}{{SA}}\)\( \Rightarrow SA = \dfrac{{OA}}{{\sin 60^\circ }} = 4a\).
Diện tích thiết diện là \({S_{SAM}} = \dfrac{1}{2}SA.SM.\sin \widehat {ASM} = \dfrac{1}{2}.4a.4a.\sin \widehat {ASM} = 8{a^2}.\sin \widehat {ASM}\)
Do \(0 < \sin \widehat {ASM} \le 1\) nên \({S_{SAM}}\) lớn nhất khi và chỉ khi \(\sin \widehat {ASM} = 1\) hay khi tam giác \(ASM\) vuông cân đỉnh \(S\) (vì \(\widehat {ASB} = 120^\circ > 90^\circ \) nên tồn tại tam giác \(ASM\) thoả mãn).
Vậy diện tích thiết diện lớn nhất là \({S_{\max }} = 8{a^2}{\mkern 1mu} \)(đvdt).
Hướng dẫn giải:
Viết biểu thức tính diện tích thiết diện và đánh giá giá trị lớn nhất của biểu thức.
