Câu hỏi:
2 năm trước
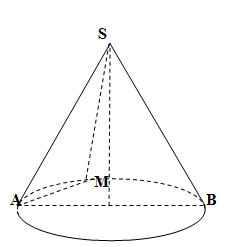
Cho hình nón đỉnh $S$, tâm đáy là $O$, góc ở đỉnh là ${135^0}$. Trên đường tròn đáy lấy điểm $A$ cố định và điểm $M$ di động. Tìm số vị trí $M$ để diện tích $SAM$ đạt giá trị lớn nhất
Trả lời bởi giáo viên
Đáp án đúng: c
Ta có:
\(\begin{array}{l}{S_{SAM}} = \dfrac{1}{2}SA.SM\sin \widehat {ASM}\\ = \dfrac{1}{2}S{A^2}\sin \widehat {ASM} \le \dfrac{1}{2}S{A^2}\\ \Rightarrow \max {S_{SAM}} = \dfrac{1}{2}S{A^2}\end{array}\)
Dấu “=” xảy ra khi \(\sin \widehat {ASM} = 1 \Leftrightarrow \widehat {ASM} = {90^0}\).
Có $2$ điểm $M$ như vậy (hai điểm đối xứng với nhau qua $AB$).
Hướng dẫn giải:
Sử dụng công thức tính diện tích tam giác \({S_{ABC}} = \dfrac{1}{2}AB.AC.\sin \widehat {BAC}\) và đánh giá \(\sin \widehat {BAC} \le 1\)