Câu hỏi:
2 năm trước
Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có đáy là hình thoi cạnh \(a\) và góc \(\widehat {BAD} = q\). Mặt chéo \(AC{C^\prime }{A^\prime }\) nằm trong mặt phẳng vuông góc với đáy, đồng thời \(AC{C^\prime }{A^\prime }\) ' là hình thoi có góc \(\widehat {{A^\prime }AC} = {60^0 }\).
Tính thể tích khối tứ diện \(AC{B^\prime }{D^\prime }\).
Trả lời bởi giáo viên
Đáp án đúng: c
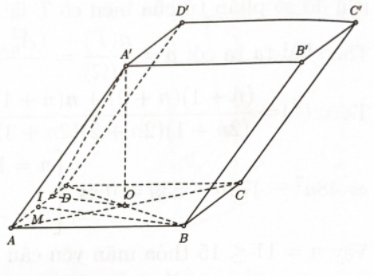
Bước 1: Tính \({S_{ABCD}};A'O\)
Ta có \({S_{ABCD}} = 2{S_{ABD}}\)\( = 2 \cdot \dfrac{1}{2}AB \cdot AD \cdot \sin {60^0 } = \dfrac{{{a^2}\sqrt 3 }}{2};\)\({A^\prime }O = \dfrac{{3a}}{2}\).
Bước 2: Tính \({V_{AC{B^\prime }{D^\prime }}} = \dfrac{1}{3}{V_{ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }}}\)
=> \({V_{AC{B^\prime }{D^\prime }}} = \dfrac{1}{3}{V_{ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }}}\)\( = \dfrac{1}{3} \cdot {A^\prime }O \cdot {S_{ABCD}}\)\( = \dfrac{1}{3} \cdot \dfrac{{3a}}{2} \cdot \dfrac{{{a^2}\sqrt 3 }}{2} = \dfrac{{{a^3}\sqrt 3 }}{4}\)
Hướng dẫn giải:
Bước 1: Tính \({S_{ABCD}};A'O\)
Bước 2: Tính \({V_{AC{B^\prime }{D^\prime }}} = \dfrac{1}{3}{V_{ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }}}\)
