Câu hỏi:
2 năm trước
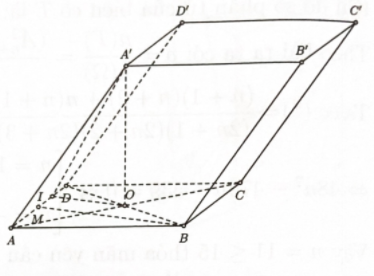
Cho hình hộp \(ABCD \cdot {A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có đáy là hình thoi cạnh \(a\) và góc \(\widehat {BAD} = q\). Mặt chéo \(AC{C^\prime }{A^\prime }\) nằm trong mặt phẳng vuông góc với đáy, đồng thời \(AC{C^\prime }{A^\prime }\) ' là hình thoi có góc \(\widehat {{A^\prime }AC} = {60^0 }\).
Tính diện toàn phần của hình nón có đáy là đường tròn nội tiếp \(\Delta ABD\) và chiều cao bằng chiều cao của lăng trụ.
Trả lời bởi giáo viên
Đáp án đúng: c
Bước 1: Tính bán kính đường tròn đáy của hình nón.
Vì \(\Delta ABD\) đều nên tâm đường tròn nội tiếp tam giác trùng với trọng tâm của tam giác
\( \Rightarrow \) Bán kính đường tròn đáy của hình nón là: \(r = \dfrac{{BM}}{3} = \dfrac{{a\sqrt 3 }}{6}\).
Bước 2: Tính diện tích xung quanh của hình nón \({S_{xq}} = \pi rl + \pi {r^2}\)
Vì chiều cao của hình nón bằng chiều cao của lăng trụ nên ta có độ dài đường sinh là
\(l = \sqrt {{A^\prime }{O^2} - {r^2}} \)\( = \sqrt {{{\left( {\dfrac{{3a}}{2}} \right)}^2} - {{\left( {\dfrac{{a\sqrt 3 }}{6}} \right)}^2}} = \dfrac{{a\sqrt {159} }}{6}\)
Vậy diện tích xung quanh của hình nón là: \({S_{xq}} = \pi rl + \pi {r^2}\)\( = \dfrac{{\pi {a^2}(\sqrt {53} + 1)}}{{12}}\).
Hướng dẫn giải:
Bước 1: Tính bán kính đường tròn đáy của hình nón.
Bước 2: Tính diện tích xung quanh của hình nón \({S_{xq}} = \pi rl + \pi {r^2}\)
