Câu hỏi:
2 năm trước
Người ta đặt được vào một hình nón hai khối cầu có bán kính lần lượt là $a$ và $2a$ sao cho các khối cầu đều tiếp xúc với mặt xung quanh của hình nón, hai khối cầu tiếp xúc với nhau và khối cầu lớn tiếp xúc với đáy của hình nón. Bán kính đáy của hình nón đã cho là:
Trả lời bởi giáo viên
Đáp án đúng: c
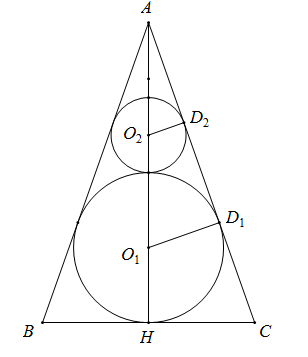
Giả sử thiết diện qua trục của hình nón là $\Delta ABC$ với $A$ là đỉnh nón, $BC$ là đường kính đáy nón.
Gọi $H$ là tâm đường tròn đáy của hình nón, ${O_1},{O_2}$ lần lượt là tâm của mặt cầu lớn và nhỏ, ${D_1},{D_2}$ lần lượt là tiếp điểm của $AC$ với $\left( {{O_1}} \right)$ và $\left( {{O_2}} \right)$.
Vì ${O_1}{D_1}//{O_2}{D_2}$ (cùng vuông góc với $AC$) nên theo hệ thức Ta – let ta có:
\( \Rightarrow \dfrac{{A{O_2}}}{{A{O_1}}} = \dfrac{{{O_2}{D_2}}}{{{O_1}{D_1}}} = \dfrac{a}{{2a}} = \dfrac{1}{2} \)
\(\Rightarrow {O_2}\) là trung điểm của \(A{O_1}\)\( \Rightarrow A{O_1} = 2{O_1}{O_2} = 2\left( {a + 2a} \right) = 6a\)
\( \Rightarrow AH = A{O_1} + {O_1}H = 6a + 2a = 8a\)
Xét tam giác vuông \(A{O_1}{D_1}\) có: \(A{D_1} = \sqrt {A{O_1}^2 - {O_1}{D_1}^2} = \sqrt {36{a^2} - 4{a^2}} = 4\sqrt 2 a\)
Dễ thấy:
$\Delta A{O_1}{D_1} \backsim \Delta ACH\,\,\left( {g.g} \right)$$ \Rightarrow \dfrac{{HC}}{{{O_1}{D_1}}} = \dfrac{{AH}}{{A{D_1}}}$$ \Rightarrow HC = \dfrac{{{O_1}{D_1}.AH}}{{A{D_1}}} = \dfrac{{2a.8a}}{{4\sqrt 2 a}} = 2\sqrt 2 a = r$
Hướng dẫn giải:
- Cắt hình nón theo mặt phẳng đi qua trục.
- Tính bán kính dựa vào định lí Pi-ta-go, định lý Ta-let và các tam giác đồng dạng.
