Mặt cầu ngoại tiếp, nội tiếp đa diện

Áp dụng công thức trên có $R = \dfrac{3}{2}$

Áp dụng các công thức trong tứ diện đều cạnh $a$

Bán kính mặt cầu nội tiếp $r = \dfrac{{a\sqrt 6 }}{{12}} = 1 \Rightarrow a = 2\sqrt 6$

Thể tích tứ diện đều đó là $V = \dfrac{{{a^3}\sqrt 2 }}{{12}} = 8\sqrt 3$

Mặt cầu nội tiếp hình lập phương cạnh $a$ có bán kính bằng $\dfrac{a}{2}$

Diện tích mặt cầu đó là $S = 4\pi {R^2} = 4\pi {\left( {\dfrac{a}{2}} \right)^2} = \pi {a^2}$

Giả sử đáy là đa giác đều ${A_1}{A_2}...{A_n}$. $O$ là tâm đáy, chóp có chiều cao là $SH$ . Gọi $I$ là trung điểm của ${A_1}{A_2}$

Ta có : $I{A_1} = R.\sin \dfrac{\pi }{n};OI = R.\cos \dfrac{\pi }{n}$

$SO = OI.\tan {60^0} = R.\cos \dfrac{\pi }{n}.\sqrt 3  = R\sqrt 3 .\cos \dfrac{\pi }{n}$

Diện tích đáy : $S = \dfrac{{3V}}{{SO}} = \dfrac{{3.\dfrac{{3\sqrt 3 }}{4}.{R^3}}}{{R\sqrt 3 .cos\dfrac{\pi }{n}}} = \dfrac{{9{R^2}}}{{4\cos \dfrac{\pi }{n}}}$

Mà $S = n.\dfrac{1}{2}{R^2}.\sin \dfrac{{2\pi }}{n} \Rightarrow \dfrac{{9{R^2}}}{{4\cos \dfrac{\pi }{n}}} = n.\dfrac{1}{2}.{R^2}.\sin \dfrac{{2\pi }}{n}$

$\Leftrightarrow n\sin \dfrac{{2\pi }}{n}\cos \dfrac{\pi }{n} = \dfrac{9}{2}$

Thử các giá trị của $n$ ở các đáp án ta được $n = 6$.

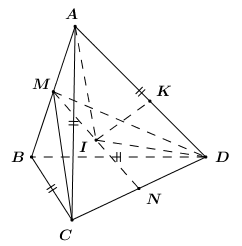
Xét các tam giác ACB, ADB lần lượt cân tại C và D nên $CM \bot AB,DM \bot AB$

Ta có : $\left\{ \begin{array}{l}\left( {ABC} \right) \cap \left( {ABD} \right) = AB\\CM \bot AB,CM \subset \left( {ABC} \right)\\DM \bot AB,DM \subset \left( {ABD} \right)\end{array} \right.$$\Rightarrow \angle \left( {\left( {ABC} \right);\left( {ABD} \right)} \right) = \angle \left( {CM;DM} \right)$.

Tam giác ACM vuông tại M nên theo Pitago ta có :

$\begin{array}{l}C{M^2} = A{C^2} - A{M^2}\\ \Rightarrow CM = \sqrt {A{C^2} - A{M^2}}  = \sqrt {{{\left( {\dfrac{{a\sqrt 3 }}{2}} \right)}^2} - {{\left( {\dfrac{a}{2}} \right)}^2}}  = \dfrac{{a\sqrt 2 }}{2}\end{array}$

Tương tự $DM = \dfrac{{a\sqrt 2 }}{2}$.

Gọi K là hình chiếu của I lên AD ta có :

Mặt cầu đường kính MN tiếp xúc với AD nên $IK = IM = IN,IK \bot AD$.

Xét tam giác AMI và AKI có :

$\begin{array}{l}\widehat {AMI} = \widehat {AKI} = {90^0};\\AI\,chung;\\IM = IK\left( {cmt} \right);\end{array}$

Do đó $\Delta AMI = \Delta AKI$ (cạnh huyền – cạnh góc vuông) $\Rightarrow AK = AM = \dfrac{a}{2}$ (cạnh tương ứng).

Tương tự : $\Delta DNI = \Delta DKI$  (cạnh huyền – cạnh  góc vuông)

$\begin{array}{l} \Rightarrow DN = DK = AD - AK = \dfrac{{a\sqrt 3 }}{2} - \dfrac{a}{2} = \dfrac{{a\left( {\sqrt 3  - 1} \right)}}{2}\\ \Rightarrow DC = 2DN = 2.\dfrac{{a\left( {\sqrt 3  - 1} \right)}}{2} = a\left( {\sqrt 3  - 1} \right)\end{array}$

Ap dụng định lý cô sin trong tam giác MCD có :

$\begin{array}{l}\cos \widehat {CMD} = \dfrac{{M{C^2} + M{D^2} - C{D^2}}}{{2MC.MD}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \dfrac{{{{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2} + {{\left( {\dfrac{{a\sqrt 2 }}{2}} \right)}^2} - {{\left( {a\left( {\sqrt 3  - 1} \right)} \right)}^2}}}{{2.\dfrac{{a\sqrt 2 }}{2}.\dfrac{{a\sqrt 2 }}{2}}}\\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2\sqrt 3  - 3 > 0\\ \Rightarrow \cos \alpha  = \cos \widehat {CMD} = 2\sqrt 3  - 3\end{array}$

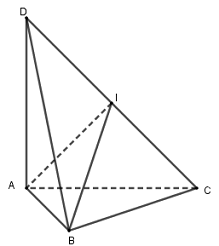
Ta có : $\left\{ \begin{array}{l}BC \bot BA\\BC \bot DA\end{array} \right. \Rightarrow BC \bot \left( {ABD} \right)$$\Rightarrow BC \bot BD$$\Rightarrow \Delta BCD$ vuông tại B.

Gọi I là trung điểm của CD thì $IB = IC = ID = \dfrac{1}{2}CD$.

Tam giác ACD vuông tại A nên $IA = IC = ID = \dfrac{1}{2}CD$.

Do đó $IA = IB = IC = ID \Rightarrow I$ là tâm mặt cầu ngoại tiếp tứ diện $ABCD$.

Tam giác ABC vuông tại B nên $AC = \sqrt {A{B^2} + B{C^2}}  = \sqrt {{3^2} + {4^2}}  = 5$  (Định lí Pytago).

Vì $DA \bot \left( {ABC} \right)$ nên $AC$ là hình chiếu của $DC$ lên $\left( {ABC} \right)$.

$\Rightarrow \angle \left( {DC;\left( {ABC} \right)} \right) = \angle \left( {DC;AC} \right) = \angle DCA = {45^0}$.

Tam giác $DAC$ vuông tại $A$ có $\widehat {DCA} = {45^0}$ nên là tam giác vuông cân $\Rightarrow DC = AC\sqrt 2  = 5\sqrt 2$.

$\Rightarrow R = IA = \dfrac{1}{2}DC = \dfrac{{5\sqrt 2 }}{2}$.

Vậy thể tích khối cầu ngoại tiếp tứ diện $ABCD$ là : $V = \dfrac{4}{3}\pi I{A^3} = \dfrac{4}{3}\pi .{\left( {\dfrac{{5\sqrt 2 }}{2}} \right)^3} = \dfrac{{125\sqrt 2 }}{3}\pi$.

Thể tích của khối cầu bằng $V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {.6^3} = 288\pi$.

Diện tích mặt cầu đã cho là:$S = 4\pi {a^2}.$

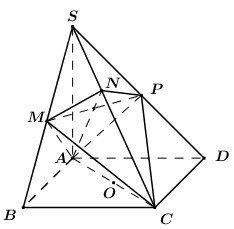
Ta có $\left\{ \begin{array}{l}BC \bot AB\\BC \bot SA\end{array} \right. \Rightarrow BC \bot \left( {SAB} \right) \Rightarrow BC \bot AM$.

$\left\{ \begin{array}{l}AM \bot BC\\AM \bot SC\end{array} \right. \Rightarrow AM \bot \left( {SBC} \right)$ $\Rightarrow AM \bot MC$.

$\Rightarrow \angle AMC = {90^0}$ hay điểm $M$ thuộc mặt cầu đường kính $AC$.

Chứng minh tương tự ta có $AP \bot \left( {SCD} \right) \Rightarrow AP \bot PC \Rightarrow \angle APC = {90^0}$ hay $P$  thuộc mặt cầu đường kính $AC$.

Lại có $AN \bot SC \Rightarrow \angle ANC = {90^0}$  hay $N$  thuộc mặt cầu đường kính $AC$.

Do đó $CMNP$ nội tiếp khối cầu đường kính $AC$ hay khối cầu ngoại tiếp tứ diện $CMNP$ có bán kính $R = \dfrac{1}{2}AC = \dfrac{1}{2}.2\sqrt 2 .\sqrt 2  = 2$.

Vậy thể tích khối cầu cần tìm là: $V = \dfrac{4}{3}\pi {R^3} = \dfrac{4}{3}\pi {.2^3} = \dfrac{{32\pi }}{3}$.

Ta có: $\dfrac{{{S_2}}}{{{S_1}}} = \dfrac{{4\pi R_2^2}}{{4\pi R_1^2}} = \dfrac{{R_2^2}}{{R_1^2}} = {2^2} = 4$.

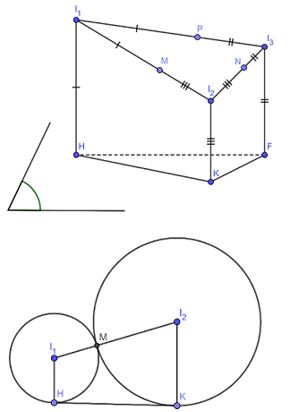
Gọi ${I_1},{I_2},{I_3}$ là tâm của các hình cầu, $M,N,P$ là các tiếp điểm của các hình cầu (như hình vẽ), $H,K,F$ là tiếp  ba hình cầu với mặt phẳng (P) (như hình vẽ).

Xét mặt phẳng $\left( {{I_1}{I_2}KH} \right)$, có:

$\begin{array}{l}HK = \sqrt {{I_1}{I_2}^2 - {{\left( {{I_2}K - {I_1}H} \right)}^2}} \,\\\,\,\,\,\,\,\,\,\, = \sqrt {{{\left( {{R_1} + {R_2}} \right)}^2} - {{\left( {{R_1} - {R_2}} \right)}^2}} \\\,\,\,\,\,\,\,\, = \sqrt {4{R_1}{R_2}}  = 2 \Rightarrow {R_1}{R_2} = 1\end{array}$

Tương tự, ${R_1}{R_3} = \dfrac{9}{4},\,{R_2}{R_3} = 4$

$\Rightarrow {R_1}{R_2}{R_3} = \sqrt {1.\dfrac{9}{4}.4}  = 3 \Rightarrow \left\{ \begin{array}{l}{R_1} = \dfrac{3}{4}\\{R_2} = \dfrac{4}{3}\\{R_3} = 3\end{array} \right.$.

Vậy ${R_1} + {R_2} + {R_3} = \dfrac{3}{4} + \dfrac{4}{3} + 3 = \dfrac{{61}}{{12}}$.

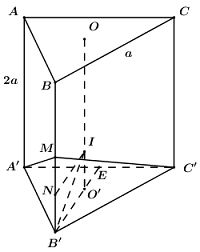
Gọi $O,\,\,O'$ lần lượt là tâm tam giác đều ABC và A’B’C’, khi đó ta có OO’ là trục của (A’B’C’).

Gọi N là trung điểm của B’M, E là trung điểm của A’C’.

Qua N kẻ NI // B’E $\left( {I \in OO'} \right)$ ta có:

$\left\{ \begin{array}{l}B'E \bot BB'\\NI\parallel B'E\end{array} \right. \Rightarrow NI \bot BB'$ $\Rightarrow IM = IB'$.

Lại có $I \in OO'$ nên $IA' = IB' = IC'$.

Do đó ta có $IA' = IB' = IC' = IM$  nên I là tâm mặt cầu ngoại tiếp chóp M.A’B’C’, bán kính $R = IB'$.

Ta có: $\left\{ \begin{array}{l}NI\parallel B'O'\\B'N\parallel O'I\end{array} \right.$ nên O’B’NI là hình bình hành $\Rightarrow O'I = B'N = \dfrac{1}{2}B'M = \dfrac{1}{4}BB' = \dfrac{a}{2}$.

Tam giác A’B’C’ đều cạnh a nên $B'E = \dfrac{{a\sqrt 3 }}{2} \Rightarrow B'O = \dfrac{2}{3}B'E = \dfrac{{a\sqrt 3 }}{3}$.

Áp dụng định lí Pytago trong tam giác vuông O’B’I có:

$IB' = \sqrt {O'{I^2} + B'O{'^2}}  = \sqrt {{{\left( {\dfrac{a}{2}} \right)}^2} + {{\left( {\dfrac{{a\sqrt 3 }}{3}} \right)}^2}}  = \dfrac{{a\sqrt {21} }}{6}$.

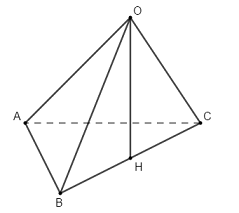
Tam giác ABC có:

$\left\{ \begin{array}{l}A{B^2} + A{C^2} = {3^2} + {4^2} = 25\\B{C^2} = {5^2} = 25\end{array} \right.$ $\Rightarrow A{B^2} + A{C^2} = B{C^2}$ $\Rightarrow \Delta ABC$ vuông tại A (Định lí Pytago đảo).

Gọi H là trung điểm của BC khi đó H là tâm đường tròn ngoại tiếp tam giác ABC, suy ra $HA = HB = HC = \dfrac{1}{2}BC = \dfrac{5}{2}.$

Mà $OA = OB = OC \Rightarrow OH \bot \left( {ABC} \right)$$\Rightarrow d\left( {O;\left( {ABC} \right)} \right) = OH = 1.$.

Áp dụng định lí Pytago trong tam giác vuông OBH có: $R = OB = \sqrt {O{H^2} + H{B^2}}  = \sqrt {1 + {{\left( {\dfrac{5}{2}} \right)}^2}}  = \dfrac{{\sqrt {29} }}{2}.$

Vậy thể tích khối cầu cần tìm là: $V = \dfrac{4}{3}\pi {R^3} = \dfrac{{29\sqrt {29} }}{6}\pi .$

Gọi ${O_1},\,\,{O_2}$ lần lượt là tâm mặt cầu $\left( {{S_1}} \right),\,\,\left( {{S_2}} \right)$. Hai mặt cầu này cắt nhau theo giao tuyến là đường tròn (C) có tâm I.

Gọi A, B là một đường kính của đường tròn giao tuyến như hình vẽ, ta có AB là trung trực của ${O_1}{O_2}$, do đó I là trung điểm của ${O_1}{O_2}$ $\Rightarrow I{O_1} = I{O_2} = \dfrac{1}{2}{O_1}{O_2} = \dfrac{R}{2} = 1$.

Thể tích phần chung chính là tổng thể tích của hai khối chỏm cầu bằng nhau có bán kính R = 2, chiều cao $h = \dfrac{R}{2} = 1$.

Vậy $V = 2.\pi {h^2}\left( {R - \dfrac{h}{3}} \right) = 2\pi {.1^2}\left( {2 - \dfrac{1}{3}} \right) = \dfrac{{10\pi }}{3}$.

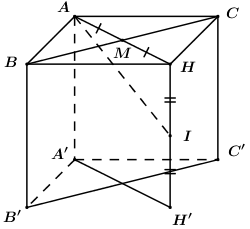
Gọi M là trung điểm của BC, H là điểm đối xứng với A qua M.

Xét tứ giác ABHC có hai đường chéo cắt nhau tại trung điểm mỗi đường và $AM \bot BC \Rightarrow AH \bot BC$ (do tam giác ABC cân tại A) nên ABHC là hình thoi $\Rightarrow HB = HC$.

Xét tam giác ABH có AB = BH, $\angle BAH = \dfrac{1}{2}\angle BAC = {60^0}$ nên là tam giác đều, do đó HA = HB.

Suy ra HA = HB = HC hay H là tâm đường tròn ngoại tiếp tam giác ABC.

Gọi H’ là hình chiếu của A lên (A’B’C’) thì H’ chính là tâm đường tròn ngoại tiếp tam giác A’B’C’, khi đó HH’ là trục của khối lăng trụ đứng.

Gọi I là trung điểm của HH’, ta có IA = IB = IC, IA’ = IB’ = IC’.

Xét tam giác vuông AHI và tam giác vuông A’H’I có: HI = H’I (theo cách dựng), AH = A’H’.

$\Rightarrow \Delta AHI = \Delta A'H'I$ (2 cạnh góc vuông) $\Rightarrow IA = IA'$. Do đó A = IB = IC = IA’ = IB’ = IC’ hay I chính là tâm mặt cầu ngoại tiếp khối lăng trụ đứng ABC.A’B’C’.

Ta có AH = AB = 2 (do ABHC là hình thoi) và HH’ = AA’ = 4 nên IH = 2.

Áp dụng định lí Pytago trong tam giác vuông AHI có: $AI = \sqrt {A{H^2} + H{I^2}}  = \sqrt {{2^2} + {2^2}}  = 2\sqrt 2$.

Suy ra bán kính mặt cầu ngoại tiếp khối lăng trụ là $R = 2\sqrt 2$.

Vậy diện tích mặt cầu ngoại tiếp khối lăng trụ là: ${S_{mc}} = 4\pi {R^2} = 4\pi .{\left( {2\sqrt 2 } \right)^2} = 32\pi$.

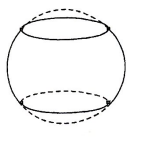
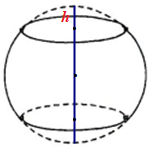
Ta có đường kính mặt cầu là $60.2 = 120\,\,\,\left( {cm} \right).$

Mà khoảng cách giữa hai đáy của thùng rượu là $80cm$

Nên chiều cao chỏm cầu là $h = \dfrac{{120 - 80}}{2} = 20\,\,\left( {cm} \right).$

Thế tích của 1 chỏm cầu chiều cao $h = 20$ và bán kính $60cm$là

${V_{cc}} = \pi {h^2}\left( {R - \dfrac{h}{3}} \right) = \pi {.20^2}\left( {60 - \dfrac{{20}}{3}} \right) = \dfrac{{64000}}{3}\pi \,\,\left( {c{m^3}} \right) = \dfrac{{64\pi }}{3}\,\,\left( l \right)$

Thể tích của cả khối cầu bán kính 60 cm là $V = \dfrac{4}{3}\pi {r^3} = \dfrac{4}{3}\pi {.60^3} = 288000\pi \,\,\left( {c{m^3}} \right) = 288\pi \,\,\left( l \right)$

Khi đó thể tích thùng rượu là $V' = V - 2{V_{cc}} = \dfrac{{736}}{3}\pi \,\,\left( l \right) \approx 771\,\,\left( l \right).$