Đường tiệm cận của đồ thị hàm số
Kỳ thi ĐGNL ĐHQG Hà Nội
Cho hàm số $y = \dfrac{{2{x^2} - 3{x} + m}}{{x - m}}$ . Để đồ thị hàm số không có tiệm cận đứng thì các giá trị của tham số $m$ là:
Cách 1: Thử đáp án
Với $m = 0$ ta có $x = 0$ là nghiệm của đa thức $2{x^2} - 3{\text{x}}$ trên tử
$ \Rightarrow y = 2{\text{x}} - 3\left( {x \ne 0} \right)$ không có tiệm cận đứng.
Với $m = 1$ ta có $x = 1$ là nghiệm của đa thức $2{x^2} - 3{\text{x + 1}}$ trên tử
$ \Rightarrow y = 2{\text{x}} - 1\left( {x \ne 1} \right)$ không có tiệm cận đứng.
Cách 2: Chia đa thức
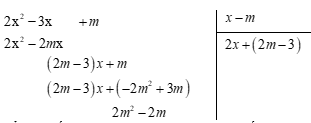
Để hàm số không có tiệm cận đứng thì tử số phải chia hết cho mẫu số
$ \Leftrightarrow 2{m^2} - 2m = 0 \Leftrightarrow m = 0$ hoặc $m = 1$
Cho hàm số \(y = f\left( x \right)\) thỏa mãn \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = - 1\) và \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = m.\) Có bao nhiêu giá trị thực của tham số \(m\) để đồ thị hàm số \(y = \dfrac{1}{{f\left( x \right) + 2}}\) có duy nhất một tiệm cận ngang.
\(\mathop {\lim }\limits_{x \to - \infty } \dfrac{1}{{f\left( x \right) + 2}} = \dfrac{1}{{\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) + \mathop {\lim }\limits_{x \to - \infty } 2}} = \dfrac{1}{{ - 1 + 2}} = 1 \Rightarrow \) Đồ thị hàm số \(y = \dfrac{1}{{f\left( x \right) + 2}}\) có TCN \(y = 1\)
\(\mathop {\lim }\limits_{x \to + \infty } \dfrac{1}{{f\left( x \right) + 2}} = \dfrac{1}{{\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) + \mathop {\lim }\limits_{x \to + \infty } 2}} = \dfrac{1}{{m + 2}}\).
Để đồ thị hàm số \(y = \dfrac{1}{{f\left( x \right) + 2}}\) có duy nhất một tiệm cận ngang thì \(\mathop {\lim }\limits_{x \to + \infty } \dfrac{1}{{f\left( x \right) + 2}}\) hoặc là không xác định hoặc là bằng 1.
Khi đó \(\left[ \begin{array}{l}m + 2 = 0\\m + 2 = 1\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = - 2\\m = - 1\end{array} \right.\).
Vậy có 2 giá trị thực của \(m\) thỏa mãn yêu cầu bài toán.
Cho hàm số \(f\left( x \right) = \dfrac{{ax + 1}}{{bx + c}}\,\,\,\left( {a,b,c \in \mathbb{R}} \right)\) có bảng biến thiên như sau:
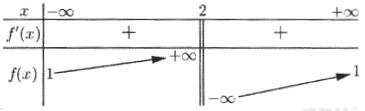
Trong các số \(a,\,\,b\) và \(c\) có bao nhiêu số dương ?
Dựa vào BBT ta thấy đồ thị hàm số có TCĐ: \(x = 2\) \( \Rightarrow - \dfrac{c}{b} = 2 \Leftrightarrow c = - 2b\)
TCN: \(y = 1 \Rightarrow \dfrac{a}{b} = 1 \Leftrightarrow a = b\)
Ta có: \(f\left( x \right) = \dfrac{{ax + 1}}{{bx + c}}\) \( \Rightarrow f'\left( x \right) = \dfrac{{ac - b}}{{{{\left( {bx + c} \right)}^2}}}\)
Hàm số đồng biến trên các khoảng \(\left( { - \infty ;2} \right)\) và \(\left( {2; + \infty } \right)\)
\(\begin{array}{l} \Leftrightarrow y' > 0\,\,\,\,\,\forall x \ne 2\\ \Leftrightarrow \dfrac{{ac - b}}{{{{\left( {bx + c} \right)}^2}}} > 0\,\,\,\forall x \ne 2\\ \Leftrightarrow ac - b > 0\\ \Leftrightarrow b.\left( { - 2b} \right) - b > 0\\ \Leftrightarrow - 2{b^2} - b > 0\\ \Leftrightarrow 2{b^2} + b < 0\\ \Leftrightarrow - \dfrac{1}{2} < b < 0\\ \Rightarrow b < 0\\ \Rightarrow a < 0,c > 0\end{array}\)
Vậy trong ba số \(a,\,\,b,\,\,c\) có 1 số dương.
Số đường tiệm cận của đồ thị hàm số \(y = \dfrac{{x - 2}}{{\sqrt {{x^2} - 4} }}\) là:
TXĐ: \(D = \left( { - \infty ; - 2} \right) \cup \left( {2; + \infty } \right)\).
Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to {2^ + }} y = \mathop {\lim }\limits_{x \to {2^ + }} \dfrac{{x - 2}}{{\sqrt {{x^2} - 4} }} = 0\\\mathop {\lim }\limits_{x \to {{\left( { - 2} \right)}^ - }} y = \mathop {\lim }\limits_{x \to {1^ - }} \dfrac{{x - 2}}{{\sqrt {{x^2} - 4} }} = - \infty \end{array}\)
Suy ra \(x = - 2\) là tiệm cận đứng của đồ thị hàm số.
\(\begin{array}{l}\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \dfrac{{x - 2}}{{\sqrt {{x^2} - 4} }} = 1\\\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{x - 2}}{{\sqrt {{x^2} - 4} }} = - 1\end{array}\)
Suy ra \(y = 1,\,\,y = - 1\) là tiệm cận ngang của đồ thị hàm số.
Vậy đồ thị hàm số đã cho có tất cả 3 đường tiệm cận.
Cho hàm số \(y = f\left( x \right)\) có bảng biến thiên như sau:

Tổng số đường tiệm cận đứng và tiệm cận ngang của đồ thị hàm số \(y = \dfrac{1}{{f\left( x \right) - 1}}\) là
Ta có: \(\mathop {\lim }\limits_{x \to + \infty } y = \mathop {\lim }\limits_{x \to + \infty } \dfrac{1}{{f\left( x \right) - 1}} = \dfrac{1}{{2 - 1}} = 1\), do đó đồ thị hàm số có TCN \(y = 1\).
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \dfrac{1}{{f\left( x \right) - 1}} = 0\), do đó đồ thị hàm số có TCN \(y = 0\).
Số đường tiệm cận đứng của đồ thị hàm số \(y = \dfrac{1}{{f\left( x \right) - 1}}\) là số nghiệm của phương trình \(f\left( x \right) = 1.\)
Dựa vào đồ thị hàm số ta thấy đường thẳng \(y = 1\) cắt đồ thị hàm số \(y = f\left( x \right)\) tại 4 điểm phân biệt nên phương trình \(f\left( x \right) = 1\) có 4 nghiệm phân biệt. Suy ra đồ thị hàm số có 4 đường tiệm cận đứng.
Vậy đồ thị hàm số có tổng cộng 6 đường tiệm cận.
Cho hàm số \(f(x) = a{x^3} + b{x^2} + cx + d\) có đồ thị như hình vẽ bên.
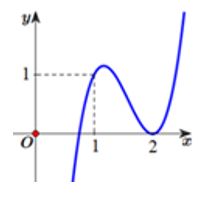
Hỏi đồ thị hàm số \(g(x) = \dfrac{{({x^2} - 3x + 2)\sqrt {x - 1} }}{{x\left[ {{f^2}(x) - f(x)} \right]}}\) có bao nhiêu tiệm cận đứng?
ĐKXĐ: \(x \ge 1,\,\,f\left( x \right) \ne 0,\,\,f\left( x \right) \ne 1\).
\(g(x) = \dfrac{{\left( {{x^2} - 3x + 2} \right)\sqrt {x - 1} }}{{x\left[ {{f^2}\left( x \right) - f\left( x \right)} \right]}} = \dfrac{{\left( {x - 2} \right)\left( {x - 1} \right)\sqrt {x - 1} }}{{x.f\left( x \right)\left( {f\left( x \right) - 1} \right)}}\)
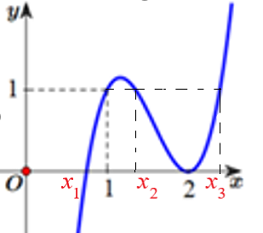
Nhận xét: \(f\left( x \right) = a{x^3} + b{x^2} + cx + d\) là hàm số bậc ba, đồng thời, quan sát đồ thị ta thấy:
+) \(f\left( x \right) = 0\) có 2 nghiệm phân biệt \(x = {x_1}\,\,\left( {0 < {x_1} < 1} \right)\,\,\left( {ktm} \right)\)(nghiệm đơn) và \(x = 2\)(nghiệm kép).
+) \(f\left( x \right) = 1\) có 3 nghiệm phân biệt \(x = 1\) (nghiệm đơn), \(x = {x_2}\,\,\left( {1 < {x_2} < 2} \right)\) (nghiệm đơn) và \(x = {x_3}\,\,\left( {{x_3} > 2} \right)\) (nghiệm đơn).
Khi đó hàm số \(y = g\left( x \right)\) được viết dưới dạng : \(g\left( x \right) = \dfrac{{\left( {x - 2} \right)\left( {x - 1} \right)\sqrt {x - 1} }}{{x.\,a\left( {x - {x_1}} \right){{\left( {x - 2} \right)}^2}.\,a\left( {x - 1} \right)\left( {x - {x_2}} \right)\left( {x - {x_3}} \right)}}\)
Do đó, đồ thị hàm số \(g\left( x \right)\) có 3 đường tiệm cận đứng là: \(x = {x_2},\,\,x = 2,\,\,x = {x_3}.\)
Biết đồ thị hàm số \(y = 2x + \sqrt {a{x^2} + bx + 4} \) có tiệm cận ngang \(y = - 1\). Giá trị \(2a - {b^3}\) bằng
\( - 56\).
\( - 56\).
\( - 56\).
Bước 1: Tìm điều kiện để đồ thị có tiệm cận ngang.
Điều kiện \(a{x^2} + bx + 4 \ge 0\). Để đồ thị hàm số có tiệm cận ngang thì \(a > 0\). Khi đó, ta có
\(\mathop {\lim }\limits_{x \to + \infty } y\)\( = \mathop {\lim }\limits_{x \to + \infty } \left( {2x + \sqrt {a{x^2} + bx + 4} } \right)\)\( = + \infty \)
\(\mathop {\lim }\limits_{x \to - \infty } y = \mathop {\lim }\limits_{x \to - \infty } \left( {2x + \sqrt {a{x^2} + bx + 4} } \right)\)\( = \mathop {\lim }\limits_{x \to - \infty } \dfrac{{(a - 4){x^2} + bx + 4}}{{\sqrt {a{x^2} + bx + 4} - 2x}} = - 1\)
Bước 2: Tìm a,b rồi tính \(2a - {b^3}\)
\( \Rightarrow \left\{ {\begin{array}{*{20}{l}}{a - 4 = 0}\\{\dfrac{b}{{ - \sqrt {a }-2 }} = - 1}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}{a = 4}\\{b = 4}\end{array}} \right.} \right.\)
Vậy \(2a - {b^3} = - 56\)

