Trung điểm của đoạn thẳng

Vì hai điểm $M;N$ cùng thuộc tia $Ox$ mà $OM < ON\left( {2cm < 3cm} \right)$ nên điểm $M$ nằm giữa hai điểm $O$ và $N$.

Do đó $OM + MN = ON \Rightarrow MN = ON - OM$ $= 3 - 2 = 1cm$

Vì hai tia $NP$ và $NO$ đối nhau mà $M$ nằm giữa hai điểm $O$ và $N$ nên $N$ là điểm nằm giữa $M$ và $P$

Do đó $MN + NP = MP$ hay $MP = 1 + 1 = 2cm$.

Vậy $MN = 1cm;\,MP = 2cm$.

$M$ là trung điểm của đoạn thẳng $AB$$\Leftrightarrow \left\{ \begin{array}{l}AM + MB = AB\\{\rm{MA  =  MB}}\end{array} \right.$

Từ câu trước và đề bài ta có  $MN = 1cm;\,MP = 2cm;\,OM = 2cm;NP = 1cm$

Suy ra $MN = NP\left( { = 1cm} \right)\,\,\,\left( 1 \right);\,MP = OM\left( { = 2cm} \right)\,\left( 2 \right)$

Lại có $M$ nằm giữa hai điểm $O$ và $N$ mà $N$ nằm giữa hai điểm $M$ và $P$ nên điểm $M$ nằm giữa hai điểm $O$ và $P$ (3)

Từ (2) và (3) ta có $M$ là trung điểm đoạn $OP.$

Theo câu trước ta có $N$ là điểm nằm giữa $M$ và $P$ nên kết hợp với $\left( 1 \right)$ suy ra $N$ là trung điểm đoạn $MP$.

Nên cả A, B đều đúng.

M là trung điểm của đoạn thẳng $AB$ khi điểm M nằm giữa hai điểm A và B, đồng thời M cách đều hai điểm A và B.

Ta có: nếu $MP = NP = \dfrac{{MN}}{2}$ thì $P$ là trung điểm của $MN$.

Suy ra P nằm giữa M và N nên A, B đều đúng.

Vì $M$ là trung điểm của đoạn thẳng $AB$ $\Leftrightarrow {\rm{MB  = }}\dfrac{1}{2}AB = \dfrac{1}{2}. 10 = 5cm$

Vậy $MB = 5cm$.

Vì $I$ là trung điểm của đoạn thẳng $MN$ nên $IM = IN = \dfrac{1}{2}MN$ hay $MN = 2. IN = 2.11 = 22cm$.

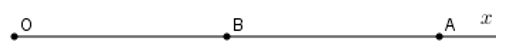
Vì hai điểm $A,B$ cùng thuộc tia $Ox$ mà $OB < OA\,\left( {4cm < 8cm} \right)$ nên điểm $B$ nằm giữa hai điểm $O$ và $A$  (1)

Do đó $OB + AB = OA$$\Rightarrow AB = OA - OB = 8 - 4 = 4cm$. Suy ra $OB = AB = 4cm$  (2)

Từ (1) và (2) suy ra $B$ là trung điểm của đoạn $OA$.

Vì $N$ là trung điểm đoạn $AM$ nên $AN = \dfrac{1}{2}AM$ hay $AM = 2AN = 2.3 = 6cm$

Lại có điểm $M$ là trung điểm đoạn thẳng $AB$ nên ta có: $AM = \dfrac{1}{2}AB$ hay $AB = 2AM = 2.6 = 12cm$

Vậy $AB = 12cm$.

Vì điểm $I$ là trung điểm đoạn thẳng $AB$ nên $AI = \dfrac{1}{2}AB = \dfrac{1}{2}. 20 = 10cm$

Vì điểm $K$ là trung điểm đoạn thẳng $AI$ nên $AK = \dfrac{1}{2}AI = \dfrac{1}{2}. 10 = 5cm$

Vậy $AI = 5cm$.

Vì điểm $B$ thuộc tia $AM$ mà $AM < AB\left( {9cm < 18cm} \right)$ nên điểm $M$ nằm giữa hai điểm $A$ và $B$ (1)

Do đó $AM + MB = AB$ $\Rightarrow MB = AB - AM = 18 - 9 = 9cm$. Suy ra $AM = MB = 9cm$ (2)

Từ (1) và (2) suy ra $M$ là trung điểm của đoạn $AB$.

Vậy B sai.

Vì $H$ là trung điểm của đoạn thẳng $MN$ nên $HN = \dfrac{1}{2}MN = \dfrac{1}{2} \cdot 7 = 3,5\,cm$.

Vì $K$ là trung điểm của đoạn thẳng $NP$ nên ${\rm{NK}} = \dfrac{1}{2}NP = \dfrac{1}{2} \cdot 11 = 5,5\,cm$.

Ta có: $N$ nằm giữa hai điểm $M$ và $P$ nên $NM$ và $NP$ là hai tia đối nhau (1)

Vì $H$ là trung điểm của $MN$ nên $H$ thuộc $NM$ (2)

Vì $K$ là trung điểm của $NP$ nên $K$ thuộc $NP$ (3)

Từ (1), (2) và (3) suy ra: $N$ là điểm nằm giữa hai điểm $H$ và $K.$

$\Rightarrow HN + NK = HK$ $\Rightarrow 3,5 + 5,5 = HK$ $\Rightarrow HK = 9\,cm.$

Từ câu trước và đề bài ta có: $MN = 4cm;\,MP = 8cm;\,OM = 4cm;NP = 4cm$

Suy ra $MN = OM\left( { = 4cm} \right)\,\,;\,NP = MN\left( { = 4cm} \right)\,$

Lại có: $M$ nằm giữa hai điểm $O$ và $N$ mà $N$ nằm giữa hai điểm $M$ và $P$ nên điểm $M$ và N lần lượt là trung điểm của đoạn ON và MP.

Nên cả A, C đều đúng.

Vì hai điểm $M;N$ cùng thuộc tia $Ox$ mà $OM < ON\left( {4cm < 8cm} \right)$ nên điểm $M$ nằm giữa hai điểm $O$ và $N$.

Do đó $OM + MN = ON \Rightarrow MN = ON - OM$ $= 8 - 4 = 4cm$

Vì hai tia $NP$ và $NO$ đối nhau mà $M$ nằm giữa hai điểm $O$ và $N$ nên $N$ là điểm nằm giữa $M$ và $P$.

Do đó $MN + NP = MP$ hay $MP = 4 + 4 = 8cm$.

Vậy $MN = 4cm;\,MP = 8cm$.

Vì $M$ là trung điểm của đoạn thẳng $OB$ nên ta có: $OM = \dfrac{1}{2}OB = \dfrac{1}{2}.10 = 5cm$

Vì $A$ và $M$ cùng thuộc tia $Ox$ mà $OM < OA\,\left( {5cm < 7cm} \right)$ nên điểm $M$ nằm giữa hai điểm $O$ và $A$.

Do đó $OM + AM = OA$ $\Rightarrow AM = OA - OM = 7 - 5 = 2cm$

Vậy $AM = 2cm.$

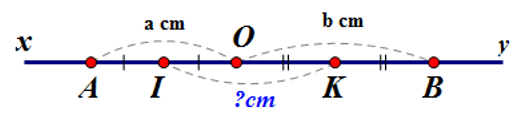
Vì $I$ là trung điểm của đoạn thẳng $OA$ nên $OI = \dfrac{1}{2}OA = \dfrac{1}{2}.a = \dfrac{a}{2}cm$

Vì $K$ là trung điểm của đoạn thẳng $OB$ nên $OK = \dfrac{1}{2}OB = \dfrac{1}{2}.b = \dfrac{b}{2}cm$

Vì $Ox$ và $Oy$ là hai tia đối nhau suy ra $OA$ và $OB$ là hai tia đối nhau.

Mà $I$ là trung điểm của đoạn thẳng $OA$ và $K$ là trung điểm của đoạn thẳng $OB$ nên $OI$ và $OK$ cũng là hai tia đối nhau suy ra điểm $O$ nằm giữa hai điểm $I$ và $K$.

Do đó $IO + OK = IK$ hay $IK = \dfrac{a}{2} + \dfrac{b}{2} = \dfrac{{a + b}}{2}cm$.

Vậy $IK = \dfrac{{a + b}}{2}cm.$

Vì điểm $M$ là trung điểm đoạn $OA$ nên $OM = \dfrac{1}{2}OA$ hay $OA = 2.OM$

Vì điểm $N$ là trung điểm đoạn $OB$ nên $ON = \dfrac{1}{2}OB$ hay $OB = 2.ON$

Mà $O$ là điểm nằm giữa $A$ và $B$ nên $OA + OB = AB$ suy ra $2.OM + 2.ON = AB$

$\Rightarrow 2.\left( {OM + ON} \right) = 24$ $\Rightarrow OM + ON = 12$ (1)

Vì $OA$ và $OB$ là hai tia đối nhau mà $M$ là trung điểm đoạn $OA$ và $N$ là trung điểm đoạn $OB$ nên $OM$ và $ON$ là hai tia đối nhau suy ra $O$ nằm giữa $M$ và $N$. Suy ra $OM + ON = MN$(2)

Từ (1) và (2) suy ra $OM + ON = MN = 12cm$.

Vậy $MN = 12cm.$

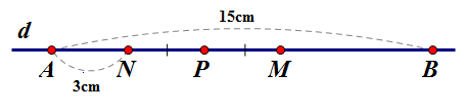
Vì điểm $N$ nằm giữa hai điểm $A,{\rm{ }}B\;$
nên $AN + NB = AB \Rightarrow NB = AB - AN = 15 - 3 = 12cm$.

Vì $M$ là trung điểm của đoạn thẳng $NB$ nên $MB = MN = \dfrac{1}{2}NB = \dfrac{1}{2}.12 = 6cm$.

Vì P là trung điểm của $MN$ nên $MP = \dfrac{1}{2}NM = \dfrac{1}{2}.6 = 3cm$.

Suy ra $MP = 3cm;MB = 6cm$.

Ta có $P$ là trung điểm của $MN$ thì $MP = NP = \dfrac{{MN}}{2}$

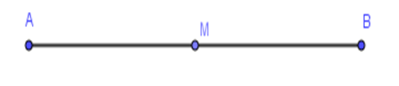
Vì $M$ là trung điểm của đoạn thẳng $AB$  $\Leftrightarrow {\rm{AM  = }}\dfrac{1}{2}AB = \dfrac{1}{2}.12 = 6cm$

Vậy $AM = 6cm$.