Hỗn số dương

Ta có: $4:3$ bằng $1$ (dư $1$ ) nên $\dfrac{4}{3} = 1\dfrac{1}{3}$

$\left( { - 2\dfrac{1}{4}} \right) + \dfrac{5}{2} =  - \dfrac{9}{4} + \dfrac{5}{2}$$= \dfrac{{ - 9}}{4} + \dfrac{{10}}{4} = \dfrac{1}{4}$

$\begin{array}{l}2\dfrac{x}{7} = \dfrac{{75}}{{35}}\\\dfrac{{2.7 + x}}{7} = \dfrac{{15}}{7}\\14 + x = 15\\x = 15 - 14\\x = 1\end{array}$

Đáp án A: $\left( { - 3\dfrac{3}{4}} \right).1\dfrac{1}{2}$$=  - \dfrac{{15}}{4}.\dfrac{3}{2} =  - \dfrac{{45}}{8} =  - 5\dfrac{5}{8} \ne  - 3\dfrac{3}{8}$

Nên A sai.

Đáp án B: $3\dfrac{3}{4}:1\dfrac{1}{5} = \dfrac{{15}}{4}:\dfrac{6}{5} = \dfrac{{15}}{4}.\dfrac{5}{6}$$= \dfrac{{25}}{8} = 3\dfrac{1}{8} \ne 3\dfrac{3}{{20}}$ nên B sai.

Đáp án C: $\left( { - 3} \right) - \left( { - 2\dfrac{2}{5}} \right)$$= \left( { - 3} \right) - \left( { - \dfrac{{12}}{5}} \right) = \left( { - 3} \right) + \dfrac{{12}}{5} = \dfrac{{ - 3}}{5}$

Nên C đúng.

Đáp án D: $5\dfrac{7}{{10}}.15 = \dfrac{{57}}{{10}}.15 = \dfrac{{171}}{2} \ne \dfrac{{105}}{2}$ nên D sai.

$M = 60\dfrac{7}{{13}}.x + 50\dfrac{8}{{13}}.x - 11\dfrac{2}{{13}}.x$

$M = \left( {60\dfrac{7}{{13}} + 50\dfrac{8}{{13}} - 11\dfrac{2}{{13}}} \right).x$

$M = \left[ {\left( {60 + 50 - 11} \right) + \left( {\dfrac{7}{{13}} + \dfrac{8}{{13}} - \dfrac{2}{{13}}} \right)} \right].x$

$M = \left( {99 + 1} \right).x = 100x$

Thay $x =  - 8\dfrac{7}{{10}}$ vào $M$ ta được:

$M = 100.\left( { - 8\dfrac{7}{{10}}} \right)$ $= 100.\left( { - \dfrac{{87}}{{10}}} \right) =  - 870$

$\begin{array}{l}6\dfrac{1}{3}:4\dfrac{2}{9} < x < \left( {10\dfrac{2}{9} + 2\dfrac{2}{5}} \right) - 6\dfrac{2}{9}\\\dfrac{{19}}{3}:\dfrac{{38}}{9} < x < \dfrac{{92}}{9} + \dfrac{{12}}{5} - \dfrac{{56}}{9}\\\dfrac{3}{2} < x < \dfrac{{32}}{5}\end{array}$

Ta có:

$\begin{array}{l}\dfrac{3}{2} < x < \dfrac{{32}}{5}\\1,5 < x < 6,4\end{array}$

Vì x là số tự nhiên nên $x \in \left\{ {2;3;4;5;6} \right\}$.

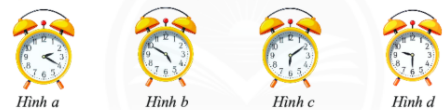
Hình a: $2\dfrac{1}{3}$

Hình b: $4\dfrac{5}{6}$

Hình c: $6\dfrac{1}{6}$

Hình d: $9\dfrac{1}{2}$

Vậy ta được các hỗn số: $2\dfrac{1}{3}$; $4\dfrac{5}{6}$; $6\dfrac{1}{6}$; $9\dfrac{1}{2}$.

a) $125\,d{m^2} = \dfrac{{125}}{{100}}{m^2} = 1\dfrac{{25}}{{100}}\,{m^2}$

b) $218\,c{m^2} = \dfrac{{218}}{{10000}}{m^2} = \dfrac{{109}}{{5000}}\,{m^2}$

c) $240\,d{m^2} = \dfrac{{240}}{{100}}{m^2} = 2\dfrac{{40}}{{100}}\,{m^2}$

d) $34\,c{m^2} = \dfrac{{34}}{{10000}}{m^2} = \dfrac{{17}}{{5000}}\,{m^2}$

Vậy ta được: $1\dfrac{{25}}{{100}}\,{m^2}$; $\dfrac{{109}}{{5000}}\,{m^2}$; $2\dfrac{{40}}{{100}}\,{m^2}$; $\dfrac{{17}}{{5000}}\,{m^2}$.

2 giờ 15 phút = $2 + \dfrac{{15}}{{60}} = 2 + \dfrac{1}{4} = 2\dfrac{1}{4}$ giờ.    

$\dfrac{{ - 9}}{{1\,\,000}} = - 0,009$

$\dfrac{{ - 5}}{8} = \dfrac{{ - 5.125}}{{8.125}} = \dfrac{{ - 625}}{{1000}} = - 0,625$

$3\dfrac{2}{{25}} = 3\dfrac{8}{{100}} = 3,08$

$- 0,125 = \dfrac{{ - 125}}{{1000}} = \dfrac{{ - 125:125}}{{1000:125}} = \dfrac{{ - 1}}{8}$

$- 0,012 = \dfrac{{ - 12}}{{1000}} = \dfrac{{ - 12:4}}{{1000:4}} = \dfrac{{ - 3}}{{250}}$

$- 4,005 = \dfrac{{ - 4005}}{{1000}} = \dfrac{{ - 4005:5}}{{1000:5}} = \dfrac{{ - 801}}{{200}}$