$BCNN(9;24)$ là bao nhiêu?
Ta có:
$\begin{array}{l}9 = {3^2};24 = {2^3}.3\\ \Rightarrow BCNN\left( {9;24} \right) = {2^3}{.3^2} = 8.9 = 72\end{array}$
Cho $36 = {2^2}{.3^2};60 = {2^2}.3.5;72 = {2^3}{.3^2}$. Ta có $UCLN(36;60;72)$là:
$36 = {2^2}{.3^2};60 = {2^2}.3.5;72 = {2^3}{.3^2}$
Ta số thừa số chung là $2;3$
Số mũ nhỏ nhất của $2$ là $2$; số mũ nhỏ nhất của $3$ là $1$
Vậy $UCLN\left( {36;60;72} \right) = {2^2}.3$.
Chọn câu đúng. $BCNN\left( {18;{\rm{ }}32;{\rm{ }}50} \right)$ là một số:
Ta có \(18 = {2.3^2};32 = {2^5};50 = {2.5^2}\)
Nên \(BCNN\left( {18;32;50} \right) = {2^5}{.3^2}{.5^2} = 7200.\)
Vì $7200$ chia hết cho $10$ nên $C$ đúng.
Tìm số tự nhiên $a, b$ thỏa mãn $\overline {2a4b} $ chia hết cho các số $2; 3; 5$ và $9.$
Ta có: Để $\overline {2a4b} $ chia hết cho $2$ và $5$ thì $b = 0\;$
Thay $b = 0\;$ vào $\overline {2a4b} $ ta được $\overline {2a40} $
Tổng các chữ số là: \(2 + a + 4 + 0 = a + 6\)
Thử lần lượt các giá trị $a = 0,1,2,...,9$
Ta thấy với \(a = 3\) thì tổng các chữ số của $\overline {2a40} = 2340$ là: \(6 + 3 = 9\, \vdots \,9\)
Nên \(2340\) chia hết cho $3$ và $9$.
Vậy với \(a = 3;b = 0\) thì \(\overline {2a4b} \) chia hết cho \(2;3;5\) và \(9.\)
Tìm số tự nhiên a lớn nhất biết: $525\,\; \vdots \;\,a;{\rm{ }}875\;\, \vdots \;\,a;{\rm{ }}280\,\; \vdots \;\,a\;$
Vì $525\,\; \vdots \;\,a;{\rm{ }}875\;\, \vdots \;\,a;{\rm{ }}280\,\; \vdots \;\,a\;$ và $a$ là số lớn nhất$ \Rightarrow a = ƯCLN\left( {525;{\rm{ }}875;{\rm{ }}280} \right)$
Ta có:
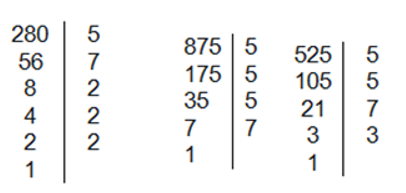
Nên \(525 = {3.5^2}.7;875 = {5^3}.7;280 = {2^3}.5.7\)
$ \Rightarrow \;a = $ ƯCLN$\left( {525;875;280} \right) = 5.7 = 35\;$
Có bao nhiêu số tự nhiên \(x\) biết \(x \vdots 5;x \vdots 6\) và \(0 < x < 100\).
Do \(x \vdots 5;x \vdots 6 \Rightarrow x \in BC\left( {5;6} \right) = \left\{ {0;30;60;90;120;...} \right\}\)
Mà \(0 < x < 100\) nên \(x \in \left\{ {30;60;90} \right\}\).
Vậy \(x \in \left\{ {30;60;90} \right\}\).
Cho $A = 18 + 36 + 72 + 2x$. Tìm giá trị của $x$ biết rằng $A$ chia hết cho $9$ và $45 < x < 55$
Ta có $A = 18 + 36 + 72 + 2x$ mà $A \vdots 9;18 \vdots 9;36 \vdots 9;72 \vdots 9 \Rightarrow 2x \vdots 9 \Rightarrow x \vdots 9$
Mà $45 < x < 55 \Rightarrow x = 54$
Vậy $x = 54$.
Một trường học có khoảng từ 100 đến 150 học sinh khối 6. Khi xếp thành 10 hàng, 12 hàng, 15 hàng đều vừa đủ. Vậy hỏi số học sinh khối 6 của trường đó là bao nhiêu?
Gọi số học sinh khối 6 là \(x\left( {x \in {N^*}} \right)\) (học sinh)
Theo bài ra ta có:
\(x \vdots 10,x \vdots 12;x \vdots 15 \Rightarrow x \in BC\left( {10;12;15} \right)\) và \(100 \le x \le 150\).
Ta có
$\begin{array}{l}10 = 2.5;12 = {2^2}.3;15 = 3.5\\ \Rightarrow BCNN(10;12;15) = {2^2}.3.5 = 60\\ \Rightarrow BC\left( {10;12;15} \right) = \left\{ {0;60;120;180;...} \right\}\\ \Rightarrow x \in \left\{ {0;60;120;180;...} \right\} \end{array}$
Mà \(100 \le x \le 150\) nên \(x = 120\).
Vậy số học sinh khổi 6 là $120$ bạn.
Một buổi liên hoan ban tổ chức đã mua tất cả 840 cái bánh, 2352 cái kẹo và 560 quả quýt chia đều ra các đĩa, mỗi đĩa gồm cả bánh, kẹo và quýt. Tính số đĩa nhiều nhất mà ban tổ chức phải chuẩn bị?
Gọi số đĩa cần chẩn bị là x cái \(\left( {x \in {N^*}} \right)\)
Vì số bánh, kẹo và quýt được chia đều vào các đĩa nên: $840\;\, \vdots x{\rm{ }};{\rm{ }}2352\,\; \vdots \;x{\rm{ }};{\rm{ }}560\;\, \vdots \;x$
Và $x$ là lớn nhất nên $x = $ƯCLN$\left( {840;2352;560} \right)$
Ta có: \(840 = {2^3}.3.5.7;560 = {2^4}.5.7;2352 = {2^4}{.3.7^2}\)
Suy ra ƯCLN$\left( {840;{\rm{ }}2352;{\rm{ }}560} \right){\rm{ }} = \;{2^3}.7\; = 56$
Vậy số đĩa nhiều nhất cần chuẩn bị là $56$ .
Cho 2 số: $14n + 3$ và $21n + 4$ với $n$ là số tự nhiên, chọn đáp án đúng.
Gọi \(d = UCLN\left( {14n + 3;21n + 4} \right)\) ta có:
\(\begin{array}{l}\left. \begin{array}{l}14n + 3\, \vdots \,d\\21n + 4 \, \vdots \, d\end{array} \right\} \Rightarrow \left. \begin{array}{l}3\left( {14n + 3} \right) \vdots \, d\\2\left( {21n + 4} \right) \vdots d\end{array} \right\} \Rightarrow \left. \begin{array}{l}42n + 9 \,\vdots \, d\\42n + 8 \, \vdots \, d\end{array} \right\}\\\Rightarrow\left( {42n + 9} \right) - \left( {42n + 8} \right) \vdots d \Rightarrow 1 \vdots d \Rightarrow d = 1\end{array}\)
Vậy \(ƯCLN\left( {14n + 3;21n + 4} \right) = 1\) hay hai số đó là hai số nguyên tố cùng nhau.

