Các dạng toán về phép nhân và phép chia phân số
Sách kết nối tri thức với cuộc sống
Phép nhân phân số có những tính chất nào?
Phép nhân phân số cũng có các tính chất tương tự phép nhân số tự nhiên như tính chất giao hoán, tính chất kết hợp, tính chất nhân phân phối.
Phân số nghịch đảo của số \( - 3\) là
Phân số nghịch đảo của số \( - 3\) là \(\dfrac{1}{{ - 3}}\)
Tính: \(\dfrac{1}{{12}} \cdot \dfrac{8}{{ - 9}}\)
$\dfrac{1}{{12}} \cdot \dfrac{8}{{ - 9}} = \dfrac{{1.8}}{{12.\left( { - 9} \right)}}$$ = \dfrac{{1.2.4}}{{4.3.\left( { - 9} \right)}} = \dfrac{2}{{ - 27}} = \dfrac{{ - 2}}{{27}}$
Kết quả của phép tính \(\dfrac{{\left( { - 7} \right)}}{6}:\left( { - \dfrac{{14}}{3}} \right)\) là phân số có tử số là
\(\dfrac{{\left( { - 7} \right)}}{6}:\left( { - \dfrac{{14}}{3}} \right) = \dfrac{{ - 7}}{6}.\dfrac{{ - 3}}{{14}} = \dfrac{{1.1}}{{2.2}} = \dfrac{1}{4}\)
Chọn câu sai.
Đáp án A: \(\dfrac{2}{7}.\dfrac{{14}}{6} = \dfrac{{2.14}}{{7.6}} = \dfrac{{28}}{{42}} = \dfrac{2}{3}\) nên A đúng.
Đáp án B: \(25.\dfrac{{ - 4}}{{15}} = \dfrac{{25.\left( { - 4} \right)}}{{15}} = \dfrac{{ - 100}}{{15}} = \dfrac{{ - 20}}{3}\) nên B đúng.
Đáp án C: \({\left( {\dfrac{2}{{ - 3}}} \right)^2}.\dfrac{9}{4} = \dfrac{{{2^2}}}{{{{\left( { - 3} \right)}^2}}}.\dfrac{9}{4}\)\( = \dfrac{4}{9}.\dfrac{9}{4} = 1\) nên C đúng.
Đáp án D: \(\dfrac{{ - 16}}{{25}}.\left( {\dfrac{{25}}{{ - 24}}} \right) = \dfrac{{ - 16}}{{25}}.\dfrac{{25}}{{ - 24}}\)\( = \dfrac{{ - 2}}{{ - 3}} = \dfrac{2}{3} \ne - \dfrac{2}{3}\) nên D sai.
Giá trị nào dưới đây của \(x\) thỏa mãn \(\left( { - \dfrac{3}{5}} \right).x = \dfrac{4}{{15}}\)?
\(\begin{array}{l}\left( { - \dfrac{3}{5}} \right).x = \dfrac{4}{{15}}\\x = \dfrac{4}{{15}}:\left( {\dfrac{{ - 3}}{5}} \right)\\x = \dfrac{4}{{15}}.\dfrac{5}{{ - 3}}\\x = - \dfrac{4}{9}\end{array}\)
Tìm số nguyên \(x\) biết \(\dfrac{{ - 5}}{6}.\dfrac{{120}}{{25}} < x < \dfrac{{ - 7}}{{15}}.\dfrac{9}{{14}}\)
\(\dfrac{{ - 5}}{6}.\dfrac{{120}}{{25}} < x < \dfrac{{ - 7}}{{15}}.\dfrac{9}{{14}}\)
\(\dfrac{{ - 5}}{6}.\dfrac{{24}}{5} < x < \dfrac{{ - 1}}{5}.\dfrac{3}{2}\)
\( - 4 < x < \dfrac{{ - 3}}{10}\)
\(x \in \left\{ { - 3; - 2; - 1} \right\}\)
Giá trị biểu thức \(M = \dfrac{5}{6}:{\left( {\dfrac{5}{2}} \right)^2} + \dfrac{7}{{15}}\) là phân số tối giản có dạng \(\dfrac{a}{b}\) với \(a > 0.\) Tính \(b + a.\)
\(\begin{array}{l}M = \dfrac{5}{6}:{\left( {\dfrac{5}{2}} \right)^2} + \dfrac{7}{{15}}\\M = \dfrac{5}{6}:\dfrac{{25}}{4} + \dfrac{7}{{15}}\\M = \dfrac{5}{6}.\dfrac{4}{{25}} + \dfrac{7}{{15}}\\M = \dfrac{{1.2}}{{3.5}} + \dfrac{7}{{15}}\\M = \dfrac{2}{{15}} + \dfrac{7}{{15}}\\M = \dfrac{9}{{15}} = \dfrac{3}{5}\end{array}\)
Khi đó \(a = 3,b = 5\) nên \(a + b = 8\)
Có bao nhiêu giá trị nguyên dương của \(x\) thỏa mãn \({\left( {\dfrac{{ - 5}}{3}} \right)^3} < x < \dfrac{{ - 24}}{{35}}.\dfrac{{ - 5}}{6}\) ?
Vì \(x\) nguyên dương nên \(x > 0\)
mà \({\left( {\dfrac{{ - 5}}{3}} \right)^3} = \dfrac{{ - 125}}{{27}} < 0\) nên
\({\left( {\dfrac{{ - 5}}{3}} \right)^3} < 0 < x <\dfrac{{ - 24}}{{35}}.\dfrac{{ - 5}}{6} \)
Khi đó:
\(0 < x < \dfrac{{ - 24}}{{35}}.\dfrac{{ - 5}}{6}\)
\(0 < x < \dfrac{4}{7}\)
Vì \(\dfrac{4}{7} < 1\) nên \(0 < x < 1\) nên không có số nguyên dương nào thỏa mãn.
Cho \(P = \left( {\dfrac{7}{{20}} + \dfrac{{11}}{{15}} - \dfrac{{15}}{{12}}} \right):\left( {\dfrac{{11}}{{20}} - \dfrac{{26}}{{45}}} \right)\) và \(Q = \dfrac{{5 - \dfrac{5}{3} + \dfrac{5}{9} - \dfrac{5}{{27}}}}{{8 - \dfrac{8}{3} + \dfrac{8}{9} - \dfrac{8}{{27}}}}:\dfrac{{15 - \dfrac{{15}}{{11}} + \dfrac{{15}}{{121}}}}{{16 - \dfrac{{16}}{{11}} + \dfrac{{16}}{{121}}}}\) . Chọn kết luận đúng:
\(P = \left( {\dfrac{7}{{20}} + \dfrac{{11}}{{15}} - \dfrac{{15}}{{12}}} \right):\left( {\dfrac{{11}}{{20}} - \dfrac{{26}}{{45}}} \right)\)
\(P = \left( {\dfrac{{21}}{{60}} + \dfrac{{44}}{{60}} - \dfrac{{75}}{{60}}} \right):\left( {\dfrac{{99}}{{180}} - \dfrac{{104}}{{180}}} \right)\)
\(P = \dfrac{{ - 10}}{{60}}:\dfrac{{ - 5}}{{180}} = \dfrac{{ - 10}}{{60}}.\dfrac{{180}}{{ - 5}} = 6\)
\(Q = \dfrac{{5 - \dfrac{5}{3} + \dfrac{5}{9} - \dfrac{5}{{27}}}}{{8 - \dfrac{8}{3} + \dfrac{8}{9} - \dfrac{8}{{27}}}}:\dfrac{{15 - \dfrac{{15}}{{11}} + \dfrac{{15}}{{121}}}}{{16 - \dfrac{{16}}{{11}} + \dfrac{{16}}{{121}}}}\)
\(Q = \dfrac{{5\left( {1 - \dfrac{1}{3} + \dfrac{1}{9} - \dfrac{1}{{27}}} \right)}}{{8\left( {1 - \dfrac{1}{3} + \dfrac{1}{9} - \dfrac{1}{{27}}} \right)}}:\dfrac{{15\left( {1 - \dfrac{1}{{11}} + \dfrac{1}{{121}}} \right)}}{{16\left( {1 - \dfrac{1}{{11}} + \dfrac{1}{{121}}} \right)}}\)
\(Q = \dfrac{5}{8}:\dfrac{{15}}{{16}} = \dfrac{5}{8}.\dfrac{{16}}{{15}} = \dfrac{2}{3}\)
Vì \(6 > \dfrac{2}{3}\) nên \(P > Q\)
Giá trị nào dưới đây của \(x\) thỏa mãn $x\;:\;\dfrac{5}{8} = \dfrac{{ - 14}}{{35}} \cdot \dfrac{{15}}{{ - 42}}$
$\begin{array}{l}x\;:\;\dfrac{5}{8} = \dfrac{{ - 14}}{{35}} \cdot \dfrac{{15}}{{ - 42}}\\x:\dfrac{5}{8} = \dfrac{{ - 2}}{5}.\dfrac{5}{{ - 14}}\\x:\dfrac{5}{8} = \dfrac{1}{7}\\x = \dfrac{1}{7}.\dfrac{5}{8}\\x = \dfrac{5}{{56}}\end{array}$
Tìm \(x\) biết \(\left( {x + \dfrac{1}{4} - \dfrac{1}{3}} \right):\left( {2 + \dfrac{1}{6} - \dfrac{1}{4}} \right) = \dfrac{7}{{46}}\)
\(\left( {x + \dfrac{1}{4} - \dfrac{1}{3}} \right):\left( {2 + \dfrac{1}{6} - \dfrac{1}{4}} \right) = \dfrac{7}{{46}}\)
\(\left( {x + \dfrac{1}{4} - \dfrac{1}{3}} \right):\dfrac{{23}}{{12}} = \dfrac{7}{{46}}\)
\(x + \dfrac{1}{4} - \dfrac{1}{3} = \dfrac{7}{{46}}.\dfrac{{23}}{{12}}\)
\(x + \dfrac{1}{4} - \dfrac{1}{3} = \dfrac{7}{{24}}\)
\(x = \dfrac{7}{{24}} - \dfrac{1}{4} + \dfrac{1}{3}\)
\(x = \dfrac{3}{8}\)
Có bao nhiêu giá trị của \(x\) thỏa mãn $\left( {\dfrac{7}{6} + x} \right):\dfrac{{16}}{{25}} = \dfrac{{ - 5}}{4}?$
$\left( {\dfrac{7}{6} + x} \right):\dfrac{{16}}{{25}} = \dfrac{{ - 5}}{4}$
\(\dfrac{7}{6} + x = \dfrac{{ - 5}}{4}.\dfrac{{16}}{{25}}\)
\(\dfrac{7}{6} + x = \dfrac{{ - 1}}{1}.\dfrac{4}{5}\)
\(\dfrac{7}{6} + x = \dfrac{{ - 4}}{5}\)
\(x = \dfrac{{ - 4}}{5} - \dfrac{7}{6}\)
\(x = \dfrac{{ - 59}}{{30}}\)
Giá trị của \(x\) thỏa mãn \(\dfrac{{13}}{{15}} - \left( {\dfrac{{13}}{{21}} + x} \right).\dfrac{7}{{12}} = \dfrac{7}{{10}}?\)
\(\dfrac{{13}}{{15}} - \left( {\dfrac{{13}}{{21}} + x} \right).\dfrac{7}{{12}} = \dfrac{7}{{10}}\)
\(\left( {\dfrac{{13}}{{21}} + x} \right).\dfrac{7}{{12}} = \dfrac{{13}}{{15}} - \dfrac{7}{{10}}\)
\(\left( {\dfrac{{13}}{{21}} + x} \right).\dfrac{7}{{12}} = \dfrac{1}{6}\)
\(\dfrac{{13}}{{21}} + x = \dfrac{1}{6}:\dfrac{7}{{12}}\)
\(\dfrac{{13}}{{21}} + x = \dfrac{2}{7}\)
\(x = \dfrac{2}{7} - \dfrac{{13}}{{21}}\)
\(x = - \dfrac{1}{3}\)
Cho \(M = \dfrac{{17}}{5}.\dfrac{{ - 31}}{{125}}.\dfrac{1}{2}.\dfrac{{10}}{{17}}.{\left( {\dfrac{{ - 1}}{2}} \right)^3}\) và \(N = \left( {\dfrac{{17}}{{28}} + \dfrac{{28}}{{29}} - \dfrac{{19}}{{30}} - \dfrac{{20}}{{31}}} \right).\left( {\dfrac{{ - 5}}{{12}} + \dfrac{1}{4} + \dfrac{1}{6}} \right)\). Khi đó tổng \(M + N\) bằng
\(M = \dfrac{{17}}{5}.\dfrac{{ - 31}}{{125}}.\dfrac{1}{2}.\dfrac{{10}}{{17}}.{\left( {\dfrac{{ - 1}}{2}} \right)^3}\)
\(M = \dfrac{{17.\left( { - 31} \right).1.10.{{\left( { - 1} \right)}^3}}}{{{{5.125.2.17.2}^3}}}\)
\(M = \dfrac{{ - 31.\left( { - 1} \right)}}{{{{125.2}^3}}}\)
\(M = \dfrac{{31}}{{1000}}\)
\(N = \left( {\dfrac{{17}}{{28}} + \dfrac{{28}}{{29}} - \dfrac{{19}}{{30}} - \dfrac{{20}}{{31}}} \right).\left( {\dfrac{{ - 5}}{{12}} + \dfrac{1}{4} + \dfrac{1}{6}} \right)\)
\(N = \left( {\dfrac{{17}}{{28}} + \dfrac{{28}}{{29}} - \dfrac{{19}}{{30}} - \dfrac{{20}}{{31}}} \right).\left( {\dfrac{{ - 5}}{{12}} + \dfrac{3}{{12}} + \dfrac{2}{{12}}} \right)\)
\(N = \left( {\dfrac{{17}}{{28}} + \dfrac{{28}}{{29}} - \dfrac{{19}}{{30}} - \dfrac{{20}}{{31}}} \right).0\)
\(N = 0\)
Vậy \(M + N = \dfrac{{31}}{{1000}} + 0 = \dfrac{{31}}{{1000}}\)
Số các số nguyên \(x\) để \(\dfrac{{5x}}{3}:\dfrac{{10{x^2} + 5x}}{{21}}\) có giá trị là số nguyên là:
\(\dfrac{{5x}}{3}:\dfrac{{10{x^2} + 5x}}{{21}}\) \( = \dfrac{{5x}}{3}.\dfrac{{21}}{{10{x^2} + 5x}}\) \( = \dfrac{{5x.21}}{{3.5x.\left( {2x + 1} \right)}}\) \( = \dfrac{7}{{2x + 1}}\)
Để biểu thức đã cho có giá trị là số nguyên thì \(\dfrac{7}{{2x + 1}}\) nguyên
Do đó \(2x + 1 \in Ư\left( 7 \right) = \left\{ { \pm 1; \pm 7} \right\}\)
Ta có bảng:
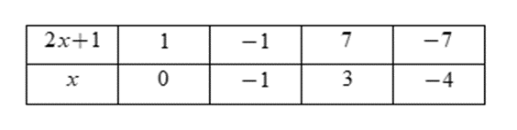
Vậy \(x \in \left\{ {0; - 1;3; - 4} \right\}\) suy ra có \(4\) giá trị thỏa mãn.
Tính: \(B = \dfrac{{{2^2}}}{3} \cdot \dfrac{{{3^2}}}{8} \cdot \dfrac{{{4^2}}}{{15}} \cdot \dfrac{{{5^2}}}{{24}} \cdot \dfrac{{{6^2}}}{{35}} \cdot \dfrac{{{7^2}}}{{48}} \cdot \dfrac{{{8^2}}}{{63}} \cdot \dfrac{{{9^2}}}{{80}}\) ta được
\(B = \dfrac{{{2^2}}}{3} \cdot \dfrac{{{3^2}}}{8} \cdot \dfrac{{{4^2}}}{{15}} \cdot \dfrac{{{5^2}}}{{24}} \cdot \dfrac{{{6^2}}}{{35}} \cdot \dfrac{{{7^2}}}{{48}} \cdot \dfrac{{{8^2}}}{{63}} \cdot \dfrac{{{9^2}}}{{80}}\)
\( = \dfrac{{2.2}}{{1.3}} \cdot \dfrac{{3.3}}{{2.4}} \cdot \dfrac{{4.4}}{{3.5}} \cdot \dfrac{{5.5}}{{4.6}} \cdot \dfrac{{6.6}}{{5.7}} \cdot \dfrac{{7.7}}{{6.8}} \cdot \dfrac{{8.8}}{{7.9}} \cdot \dfrac{{9.9}}{{8.10}}\)
\( = \dfrac{{2.3.4.5.6.7.8.9}}{{1.2.3.4.5.6.7.8.}} \cdot \dfrac{{2.3.4.5.6.7.8.9}}{{3.4.5.6.7.8.9.10}}\)
\( = \dfrac{9}{1} \cdot \dfrac{2}{{10}} = \dfrac{{9.2}}{{1.10}} = \dfrac{9}{5}\)
Một người đi xe máy, đi đoạn đường AB với vận tốc \(40km/h\) hết \(\dfrac{5}{4}\) giờ. Lúc về, người đó đi với vận tốc \(45km/h\). Tính thời gian người đó đi từ B về A?
Quãng đường AB là: \(40.\dfrac{5}{4} = 50\) (km)
Thời gian người đó đi từ B về A là: \(\dfrac{{50}}{{45}} = \dfrac{{10}}{9}\) (giờ)
Phân số \(\dfrac{a}{b}\) là phân số lớn nhất mà khi chia mỗi phân số \(\dfrac{{12}}{{35}};\) \(\dfrac{{18}}{{49}}\) cho \(\dfrac{a}{b}\) ta được kết quả là một số nguyên. Tính \(a + b.\)
Gọi phân số lớn nhất cần tìm là: \(\dfrac{a}{b}\) (\(a;b\) là nguyên tố cùng nhau)
Ta có: \(\dfrac{{12}}{{35}}:\dfrac{a}{b} = \dfrac{{12b}}{{35{\rm{a}}}}\) là số nguyên, mà \(12;35\) là nguyên tố cùng nhau
Nên \(12 \vdots a;b \vdots 35\)
Ta lại có: \(\dfrac{{18}}{{49}}:\dfrac{a}{b} = \dfrac{{18b}}{{49{\rm{a}}}}\) là số nguyên, mà \(18\) và \(49\) nguyên tố cùng nhau
Nên \(18 \vdots a;b \vdots 49\)
Để \(\dfrac{a}{b}\) lớn nhất ta có \(a = UCLN(12;18) = 6\) và \(b = BCNN(35;49) = 245\)
Vậy tổng \(a + b = 6 + 245 = 251\)
Tìm số tự nhiên \(x\) biết \(\dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{x\left( {x + 1} \right):2}} = \dfrac{{2019}}{{2021}}\)
\(\begin{array}{l}\dfrac{1}{3} + \dfrac{1}{6} + \dfrac{1}{{10}} + ... + \dfrac{1}{{x\left( {x + 1} \right):2}} = \dfrac{{2019}}{{2021}}\\2.\left[ {\dfrac{1}{{2.3}} + \dfrac{1}{{3.4}} + ... + \dfrac{1}{{x(x + 1)}}} \right] = \dfrac{{2019}}{{2021}}\\2.\left( {\dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{3} - \dfrac{1}{4} + ... + \dfrac{1}{x} - \dfrac{1}{{x + 1}}} \right) = \dfrac{{2019}}{{2021}}\\2.\left( {\dfrac{1}{2} - \dfrac{1}{{x + 1}}} \right) = \dfrac{{2019}}{{2021}}\\1 - \dfrac{2}{{x + 1}} = \dfrac{{2019}}{{2021}}\\\dfrac{2}{{x + 1}} = 1 - \dfrac{{2019}}{{2021}}\\\dfrac{2}{{x + 1}} = \dfrac{2}{{2021}}\\x + 1 = 2021\\x = 2020\end{array}\)
