Câu hỏi:
2 năm trước
Trên đường thẳng \(d\) vẽ đoạn thẳng \(AB = 15cm.\) Lấy điểm \(N\) nằm giữa hai điểm \(A,{\rm{ }}B\) và \(AN = 3cm.\) Gọi \(M\) là trung điểm của đoạn thẳng \(BN,\) gọi \(P\) là trung điểm của đoạn thẳng \(MN.\) Tính độ dài \(MP\) và \(MB.\)
Trả lời bởi giáo viên
Đáp án đúng: a
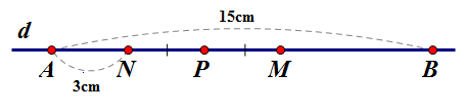
Vì điểm \(N\) nằm giữa hai điểm \(A,{\rm{ }}B\;\)
nên \(AN + NB = AB \Rightarrow NB = AB - AN = 15 - 3 = 12cm\).
Vì \(M\) là trung điểm của đoạn thẳng \(NB\) nên \(MB = MN = \dfrac{1}{2}NB = \dfrac{1}{2}.12 = 6cm\).
Vì P là trung điểm của \(MN\) nên \(MP = \dfrac{1}{2}NM = \dfrac{1}{2}.6 = 3cm\).
Suy ra \(MP = 3cm;MB = 6cm\).
Hướng dẫn giải:
+ Vì điểm \(N\) nằm giữa hai điểm \(A,{\rm{ }}B\)
Áp dụng tính chất cộng độ dài đoạn thẳng để tính \(NB\)
+ Vì \(M\) là trung điểm của đoạn thẳng \(NB\) nên tính được \(MN\) dựa vào tính chất trung điểm của đoạn thẳng.
+ Vì P là trung điểm của \(MN\) nên tính được \(NP\) dựa vào tính chất trung điểm của đoạn thẳng.
Câu hỏi khác
- Bài tập điềm nằm giữa hai điểm. tia môn toán 6 sách KNTT có lời giải
- Bài tập điểm và đường thẳng môn toán 6 sách KNTT có lời giải
- Bài tập trung điểm của đoạn thẳng môn toán 6 sách KNTT có lời giải
- Bài tập đoạn thẳng. độ dài đoạn thẳng môn toán 6 sách KNTT có lời giải
- Bài tập góc môn toán 6 sách KNTT có lời giải
