Trung điểm của đoạn thẳng

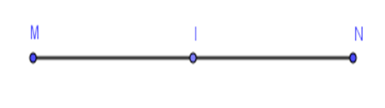
Vì $I$ là trung điểm của đoạn thẳng $MN$ nên $IM = IN = \dfrac{1}{2}MN$ hay $MN = 2.IN = 2.8 = 16cm$.

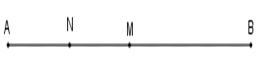
Vì $N$ là trung điểm đoạn $AM$ nên $AN = \dfrac{1}{2}AM$ hay $AM = 2AN = 2.1,5 = 3cm$

Lại có điểm $M$ là trung điểm đoạn thẳng $AB$ nên ta có $AM = \dfrac{1}{2}AB$ hay $AB = 2AM = 2.3 = 6cm$

Vậy $AB = 6cm$.

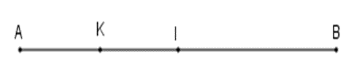
Vì điểm $I$ là trung điểm đoạn thẳng $AB$ nên $AI = \dfrac{1}{2}AB = \dfrac{1}{2}.8 = 4cm$

Vì điểm $K$ là trung điểm đoạn thẳng $AI$ nên $AK = \dfrac{1}{2}AI = \dfrac{1}{2}.4 = 2cm$

Vậy  $AI = 2cm$.

Vì $H$ là trung điểm của đoạn thẳng $MN$ nên $HN = \dfrac{1}{2}MN = \dfrac{1}{2} \cdot 5 = 2,5\,cm$.

Vì $K$ là trung điểm của đoạn thẳng $NP$ nên ${\rm{NK}} = \dfrac{1}{2}NP = \dfrac{1}{2} \cdot 9 = 4,5\,cm$.

Ta có $N$ nằm giữa hai điểm $M$ và $P$ nên $NM$ và $NP$ là hai tia đối nhau. (1)

Vì $H$ là trung điểm của $MN$ nên $H$ thuộc $NM$ (2)

Vì $K$ là trung điểm của $NP$ nên $K$ thuộc $NP$ (3)

Từ (1), (2) và (3) suy ra $N$ là điểm nằm giữa hai điểm $H$ và $K.$

\( \Rightarrow HN + NK = HK \Rightarrow 2,5 + 4,5 = HK\) \( \Rightarrow HK = 7\,cm.\)

Vì $M$ là trung điểm của đoạn thẳng $OB$ nên ta có $OM = \dfrac{1}{2}OB = \dfrac{1}{2}.5 = 2,5cm$

Vì $A$ và $M$ cùng thuộc tia $Ox$ mà $OA < OM\,\left( {2cm < 2,5cm} \right)$ nên điểm $A$ nằm giữa hai điểm $O$ và $M$.

Do đó $OA + AM = OM$ $ \Rightarrow AM = OM - OA = 2,5 - 2 = 0,5cm$

Vậy $AM = 0,5cm.$

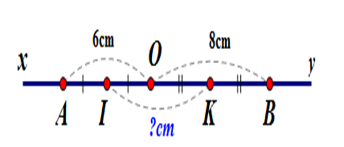
Vì $I$ là trung điểm của đoạn thẳng $OA$ nên $OI = \dfrac{1}{2}OA = \dfrac{1}{2}.6 = 3cm$

Vì $K$ là trung điểm của đoạn thẳng $OB$ nên $OK = \dfrac{1}{2}OB = \dfrac{1}{2}.8 = 4cm$

Vì $Ox$ và $Oy$ là hai tia đối nhau suy ra $OA$ và $OB$ là hai tia đối nhau.

Mà $I$ là trung điểm của đoạn thẳng $OA$ và $K$ là trung điểm của đoạn thẳng $OB$ nên $OI$ và $OK$ cũng là hai tia đối nhau suy ra điểm $O$ nằm giữa hai điểm $I$ và $K$.

Do đó $IO + OK = IK$ hay $IK = 3 + 4 = 7cm$.

Vậy $IK = 7cm.$

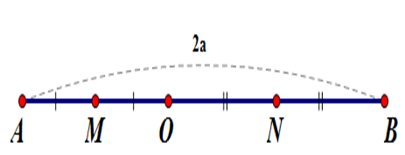
Vì điểm $M$ là trung điểm đoạn $OA$ nên $OM = \dfrac{1}{2}OA$ hay $OA = 2.OM$

Vì điểm $N$ là trung điểm đoạn $OB$ nên $ON = \dfrac{1}{2}OB$ hay $OB = 2.ON$

Mà $O$ là điểm nằm giữa $A$ và $B$ nên $OA + OB = AB$ suy ra $2.OM + 2.ON = AB$

$ \Rightarrow 2.\left( {OM + ON} \right) = 2a$ $ \Rightarrow OM + ON = a$ (1)

Vì $OA$ và $OB$ là hai tia đối nhau mà $M$ là trung điểm đoạn $OA$ và $N$ là trung điểm đoạn $OB$ nên $OM$ và $ON$ là hai tia đối nhau suy ra $O$ nằm giữa $M$ và $N$. Suy ra $OM + ON = MN$(2)

Từ (1) và (2) suy ra $OM + ON = MN = a$

Vậy $MN = a.$

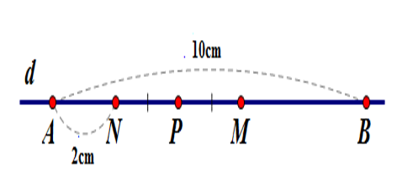
Vì điểm $N$ nằm giữa hai điểm $A,{\rm{ }}B\;$
nên $AN + NB = AB \Rightarrow NB = AB - AN = 10 - 2 = 8cm$

Vì $M$ là trung điểm của đoạn thẳng $NB$ nên $MN = \dfrac{1}{2}NB = \dfrac{1}{2}.8 = 4cm$

Vì $P$ là trung điểm của $MN$ nên $MP = \dfrac{1}{2}NM = \dfrac{1}{2}.4 = 2cm$

Suy ra $MP = 2cm;AN = 2cm$ nên $MP = AN.$

Vì hai điểm $M;N$ cùng thuộc tia $Ox$ mà $OM < ON\left( {2cm < 3cm} \right)$ nên điểm $M$ nằm giữa hai điểm $O$ và $N$.

Do đó $OM + MN = ON \Rightarrow MN = ON - OM$ $ = 3 - 2 = 1cm$

Vì hai tia $NP$ và $NO$ đối nhau mà $M$ nằm giữa hai điểm $O$ và $N$ nên $N$ là điểm nằm giữa $M$ và $P$

Do đó $MN + NP = MP$ hay $MP = 1 + 1 = 2cm$.

Vậy $MN = 1cm;\,MP = 2cm$.

Từ câu trước và đề bài ta có  $MN = 1cm;\,MP = 2cm;\,OM = 2cm;NP = 1cm$

Suy ra $MN = NP\left( { = 1cm} \right)\,\,\,\left( 1 \right);\,MP = OM\left( { = 2cm} \right)\,\left( 2 \right)$

Lại có $M$ nằm giữa hai điểm $O$ và $N$ mà $N$ nằm giữa hai điểm $M$ và $P$ nên điểm $M$ nằm giữa hai điểm $O$ và $P$ (3)

Từ (2) và (3) ta có $M$ là trung điểm đoạn $OP.$

Theo câu trước ta có $N$ là điểm nằm giữa $M$ và $P$ nên kết hợp với $\left( 1 \right)$ suy ra $N$ là trung điểm đoạn $MP$.

Nên cả A, B đều đúng.

Ta có điểm $C$ thuộc tia $Ox$, điểm $D$ thuộc tia $Oy$ mà hai tia $Ox;Oy$ đối nhau nên điểm $O$ nằm giữa hai điểm $C$ và $D$ mà $OC = OD$ (đề bài) nên điểm $O$ là trung điểm đoạn $CD.$  (do đó A đúng)

Trên tia $Ox$ vì $OC < OI$ nên $C$ nằm giữa $O$ và $I$ (do đó C đúng)

Suy ra $OI = IC + OC \Rightarrow IC = OI - OC\,\left( 1 \right)$

Vì $O$ nằm giữa hai điểm $C$ và $D$ (cmt) mà $C$ nằm giữa $O$ và $I$ nên $O$ nằm giữa $I$ và $D$.

Ta có $ID = OI + OD\,\left( 2 \right)$ mà $OC = OD\,\left( 3 \right)$

Từ (1); (2);(3) ta có $IC + ID $$= OI - OC + OI + OD $$= 2OI - OC + OC = 2OI$

Hay $IC + ID = 2OI.$ Do đó B đúng, D sai.

Ta có: điểm M là trung điểm đoạn AB nên M nằm giữa A và B, đồng thời \(MA = MB = \dfrac{{AB}}{2}\).

Ta có: hai tia BM và BA trùng nhau, tia BO và BA đối nhau nên hai tia BO và BM đối nhau hay B nằm giữa  hai điểm O và M. Nên ta có: \(OB + BM = OM\) hay \(OM = OB + AM\)  (1)

Lại có: hai tia MA và MB đối nhau, hai tia MB, MO trùng nhau nên hai tia MA, MO đối nhau. Do đó M nằm giữa A và O. Suy ra \(AM + MO = AO \Rightarrow OM = AO - MA\)  (2)

Từ (1) và (2) suy ra: \(2OM = OA + OB + AM - AM\) hay \(OM = \dfrac{{OA + OB}}{2}.\)