Câu hỏi:
2 năm trước
Trên đường thẳng $d$ vẽ đoạn thẳng $AB = 10cm.$ Lấy điểm $N$ nằm giữa hai điểm $A,{\rm{ }}B$ và $AN = 2cm.$ Gọi $M$ là trung điểm của đoạn thẳng $BN,$ gọi $P$ là trung điểm của đoạn thẳng $MN.$ So sánh \(MP\) và \(AN.\)
Trả lời bởi giáo viên
Đáp án đúng: c
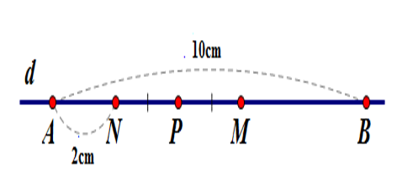
Vì điểm $N$ nằm giữa hai điểm $A,{\rm{ }}B\;$
nên $AN + NB = AB \Rightarrow NB = AB - AN = 10 - 2 = 8cm$
Vì $M$ là trung điểm của đoạn thẳng $NB$ nên $MN = \dfrac{1}{2}NB = \dfrac{1}{2}.8 = 4cm$
Vì $P$ là trung điểm của $MN$ nên $MP = \dfrac{1}{2}NM = \dfrac{1}{2}.4 = 2cm$
Suy ra $MP = 2cm;AN = 2cm$ nên $MP = AN.$
Hướng dẫn giải:
+ Vì điểm $N$ nằm giữa hai điểm $A,{\rm{ }}B\;$
Áp dụng tính chất cộng độ dài đoạn thẳng để tính $NB$
+ Vì $M$ là trung điểm của đoạn thẳng $NB$ nên tính được $MN$ dựa vào tính chất trung điểm của đoạn thẳng
+ Vì $P$ là trung điểm của $MN$ nên tính được $NP$ dựa vào tính chất trung điểm của đoạn thẳng
Câu hỏi khác
- Bài tập điềm nằm giữa hai điểm. tia môn toán 6 sách KNTT có lời giải
- Bài tập điểm và đường thẳng môn toán 6 sách KNTT có lời giải
- Bài tập trung điểm của đoạn thẳng môn toán 6 sách KNTT có lời giải
- Bài tập đoạn thẳng. độ dài đoạn thẳng môn toán 6 sách KNTT có lời giải
- Bài tập góc môn toán 6 sách KNTT có lời giải
