Khoảng cách từ điểm đến mặt phẳng
Kỳ thi ĐGNL ĐHQG Hà Nội
Cho hình lập phương \(ABCD,{A^\prime }{B^\prime }{C^\prime }{D^\prime }\) có cạnh bằng 3a. Khoảng cách từ \({A^\prime }\) đến mặt phẳng \((ABCD)\) bằng
Ta có \(A'A \bot \left( {ABCD} \right) \Rightarrow d\left( {A',\left( {ABCD} \right)} \right) = A'A\)$=3a$.
Cho hình chóp \(S.ABCD\) có đáy \(ABCD\) là hình chữ nhật, \(AB = a,\) \(AD = 2a\). Tam giác \(SAB\) cân tại \(S\) và nằm trong mặt phẳng vuông góc với đáy. Góc giữa \(SC\) và mặt phẳng \(\left( {ABCD} \right)\) bằng \({45^0}\). Gọi \(M\) là trung điểm \(SD\), hãy tính theo \(a\) khoảng cách \(d\) từ \(M\) đến mặt phẳng \(\left( {SAC} \right)\).
Đáp án:
Đáp án:
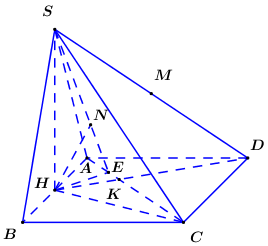
Bước 1: Đổi \(d\left( {M;\left( {SAC} \right)} \right)\) sang \(d\left( {H;\left( {SAC} \right)} \right)\).
Gọi \(H\) là trung điểm \(AB\). Vì \(\Delta SAB\) cân tại \(S\) nên \(SH \bot AB\).
Ta có: \(\left\{ \begin{array}{l}\left( {SAB} \right) \cap \left( {ABCD} \right) = AB\\SH \subset \left( {ABCD} \right),\,\,SH \bot AB\end{array} \right.\) \( \Rightarrow SH \bot \left( {ABCD} \right)\).
Gọi \(K = HD \cap AC\). Áp dụng định lí Ta-let ta có \(\dfrac{{DK}}{{HK}} = \dfrac{{DC}}{{AH}} = 2 \Rightarrow DK = 2HK\).
Ta có \(MD \cap \left( {SAC} \right) = S \Rightarrow \dfrac{{d\left( {M;\left( {SAC} \right)} \right)}}{{d\left( {D;\left( {SAC} \right)} \right)}} = \dfrac{{SM}}{{SD}} = \dfrac{1}{2}\)
\( \Rightarrow d\left( {M;\left( {SAC} \right)} \right) = \dfrac{1}{2}d\left( {D;\left( {SAC} \right)} \right)\)
Lại có \(DH \cap \left( {SAC} \right) = K\) nên \(\dfrac{{d\left( {D;\left( {SAC} \right)} \right)}}{{d\left( {H;\left( {SAC} \right)} \right)}} = \dfrac{{DK}}{{HK}} = 2 \Rightarrow d\left( {D;\left( {SAC} \right)} \right) = 2d\left( {H;\left( {SAC} \right)} \right)\)
Bước 2: Trong \(\left( {ABCD} \right)\) kẻ \(HE \bot AC\,\,\left( {E \in AC} \right)\), trong \(\left( {SHE} \right)\) kẻ \(HN \bot SE\,\,\left( {N \in SE} \right)\), chứng minh \(HN \bot \left( {SAC} \right)\)
Do đó \(d\left( {M;\left( {SAC} \right)} \right) = d\left( {H;\left( {SAC} \right)} \right)\)
Trong \(\left( {ABCD} \right)\) kẻ \(HE \bot AC\,\,\left( {E \in AC} \right)\), trong \(\left( {SHE} \right)\) kẻ \(HN \bot SE\,\,\left( {N \in SE} \right)\) ta có:
\(\left\{ \begin{array}{l}AC \bot HE\\AC \bot SH\end{array} \right. \Rightarrow AC \bot \left( {SHE} \right) \)\(\Rightarrow AC \bot HN\)\(\left\{ \begin{array}{l}HN \bot SE\\HN \bot AC\end{array} \right. \Rightarrow HN \bot \left( {SAC} \right)\)\( \Rightarrow d\left( {H;\left( {SAC} \right)} \right) = HN\)
Bước 3: Xác định góc giữa \(SC\) và \(\left( {ABCD} \right)\), từ đó tính \(SH\).
Vì \(SH \bot \left( {ABCD} \right)\) nên \(HC\) là hình chiếu vuông góc của \(SC\) lên \(\left( {ABCD} \right)\)
\( \Rightarrow \angle \left( {SC;\left( {ABCD} \right)} \right) = \angle \left( {SC;HC} \right) = \angle SCH = {45^0}\)
\( \Rightarrow \Delta SHC\) vuông cân tại \(H\)\( \Rightarrow SH = HC = \sqrt {B{C^2} + B{H^2}} \)\(= \sqrt {{{\left( {2a} \right)}^2} + {{\left( {\dfrac{a}{2}} \right)}^2}} = \dfrac{{a\sqrt {17} }}{2}\)
Bước 4: Tính \(d\left( {M;\left( {SAC} \right)} \right) \)
Ta có: \({S_{HAC}} = \dfrac{1}{2}HE.AC = \dfrac{1}{2}{S_{ABC}}\)
$\Rightarrow HE.AC = \dfrac{1}{2}.AB.BC$
$ \Rightarrow HE = \dfrac{{\dfrac{1}{2}.AB.BC}}{{AC}} $$= \dfrac{{\dfrac{1}{2}.a.2a}}{{\sqrt {{a^2} + {{\left( {2a} \right)}^2}} }} $$= \dfrac{a}{{\sqrt 5 }}$
Áp dụng hệ thức lượng trong tam giác vuông \(SHE\) ta có:
Nên \(HN = \dfrac{{SH.HE}}{{\sqrt {S{H^2} + H{E^2}} }} = \dfrac{{\dfrac{{a\sqrt {17} }}{2}.\dfrac{a}{{\sqrt 5 }}}}{{\sqrt {\dfrac{{17{a^2}}}{4} + \dfrac{{{a^2}}}{5}} }} = \dfrac{{a\sqrt {1513} }}{{89}}\)
Vậy \(d\left( {M;\left( {SAC} \right)} \right) = \dfrac{{a\sqrt {1513} }}{{89}}\).
Cho tứ diện \(OABC\) có ba cạnh \(OA,\,\,OB,\,\,OC\) đôi một vuông góc với nhau. Biết khoảng cách từ điểm \(O\) đến các đường thẳng \(BC,\,\,CA,\,\,AB\) lần lượt là \(a,\,\,a\sqrt 2 ,\,\,a\sqrt 3 \). Khoảng cách từ điểm \(O\) đến mặt phẳng \(\left( {ABC} \right)\) là \(\dfrac{{2a\sqrt {m} }}{{11}}\). Tìm $m$.
Đáp án:
Đáp án:
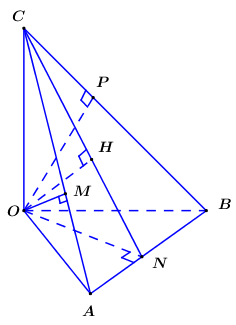
Bước 1: Kẻ \(OM \bot AC\,\,\left( {M \in AC} \right)\), \(ON \bot AB\,\,\left( {N \in AB} \right)\), \(OP \bot BC\,\,\left( {P \in BC} \right)\).
Kẻ \(OM \bot AC\,\,\left( {M \in AC} \right)\), \(ON \bot AB\,\,\left( {N \in AB} \right)\), \(OP \bot BC\,\,\left( {P \in BC} \right)\).
Khi đó ta có \(OP = a,\,\,OM = a\sqrt 2 ,\,\,ON = a\sqrt 3 \).
Bước 2: Trong \(\left( {OCN} \right)\) kẻ \(OH \bot CN\,\,\left( {H \in CN} \right)\), chứng minh \(OH \bot \left( {ABC} \right)\).
Trong \(\left( {OCN} \right)\) kẻ \(OH \bot CN\,\,\left( {H \in CN} \right)\) ta có:
\(\begin{array}{l}\left\{ \begin{array}{l}AB \bot ON\\AB \bot OC\end{array} \right. \Rightarrow AB \bot \left( {OCN} \right) \Rightarrow AB \bot OH\\\left\{ \begin{array}{l}OH \bot AB\\OH \bot CN\end{array} \right. \Rightarrow OH \bot \left( {ABC} \right) \Rightarrow d\left( {O;\left( {ABC} \right)} \right) = OH\end{array}\)
Bước 3: Sử dụng hệ thức lượng trong tam giác vuông để tính khoảng cách.
Áp dụng hệ thức lượng trong tam giác vuông ta có: \(\dfrac{1}{{O{H^2}}} = \dfrac{1}{{O{C^2}}} + \dfrac{1}{{O{N^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}\)
Lại có
\(\begin{array}{l}\dfrac{1}{{O{M^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{C^2}}};\,\,\dfrac{1}{{O{N^2}}} = \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}};\,\,\dfrac{1}{{O{P^2}}} = \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}\\ \Rightarrow \dfrac{1}{{O{M^2}}} + \dfrac{1}{{O{N^2}}} + \dfrac{1}{{O{P^2}}} = 2\left( {\dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}}} \right)\\ \Rightarrow \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}} = \dfrac{1}{2}\left( {\dfrac{1}{{O{M^2}}} + \dfrac{1}{{O{N^2}}} + \dfrac{1}{{O{P^2}}}} \right)\\ \Rightarrow \dfrac{1}{{O{A^2}}} + \dfrac{1}{{O{B^2}}} + \dfrac{1}{{O{C^2}}} = \dfrac{1}{2}\left( {\dfrac{1}{{2{a^2}}} + \dfrac{1}{{3{a^2}}} + \dfrac{1}{{{a^2}}}} \right) = \dfrac{{11}}{{12{a^2}}}\\ \Rightarrow \dfrac{1}{{O{H^2}}} = \dfrac{{11}}{{12{a^2}}} \Rightarrow OH = \dfrac{{2a\sqrt {33} }}{{11}}\end{array}\)
=> \(d\left( {O;\left( {ABC} \right)} \right) = \dfrac{{2a\sqrt {33} }}{{11}}\).
Vậy m=33.
Cho hình chóp $S . A B C D$ có đáy $A B C D$ là hình thoi cạnh $a .$ Tam giác $A B C$ đều, hình chiếu vuông góc $H$ của đỉnh $S$ trên mặt phẳng $(A B C D)$ trùng với trọng tâm của tam giác $A B C$. Đường thẳng $S D$ hợp với mặt phẳng $(A B C D)$ một góc $30^{\circ}$. Tính khoảng cách $d$ từ $B$ đến mặt phẳng $(S C D)$ theo $a$
$d=\dfrac{ a \sqrt{21}}{7}$
$d=\dfrac{ a \sqrt{21}}{7}$
$d=\dfrac{ a \sqrt{21}}{7}$
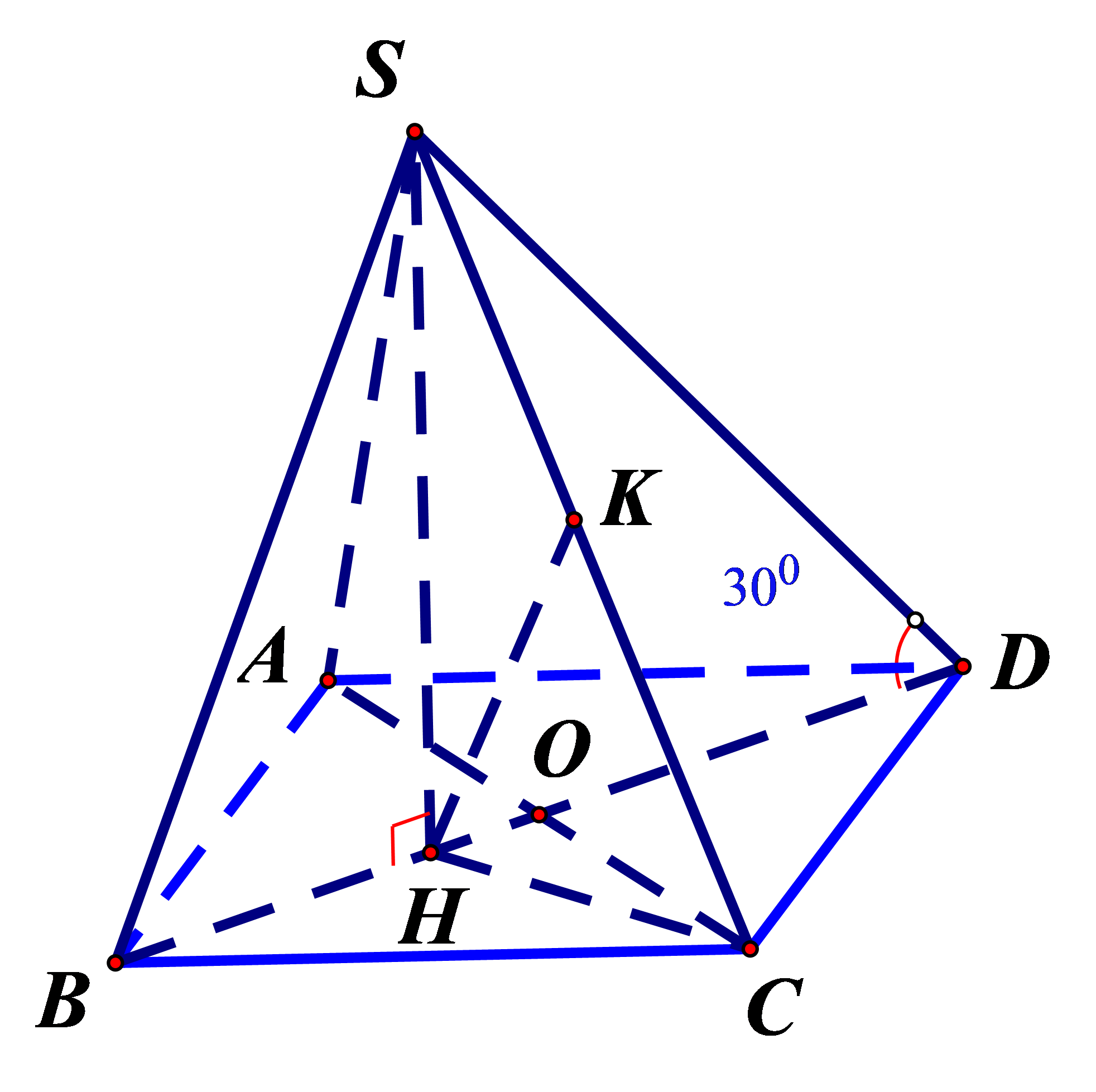
Bước 1: Gọi $O=A C \cap B D$. Tính BO, CH, HD theo a.
Gọi $O=A C \cap B D$
Ta có $\Delta A B C$ dều cạnh $a$ có $H$ là trọng tâm $\Rightarrow B O=\dfrac{a \sqrt{3}}{2}, C H=\dfrac{a \sqrt{3}}{3}, H D=\dfrac{4}{3} B O=\dfrac{2 a \sqrt{3}}{3}$
Bước 2: Tính SH theo a.
Mặt khác, $(\widehat{S D,(A B C D)})=\widehat{S D H}=30^{\circ}$
$\Rightarrow S H=H D \cdot \tan \widehat{S D H}=\dfrac{2 a}{3}$
Lại có $C H \perp A B \Rightarrow C H \perp C D$
Bước 3: Kẻ $H K \perp S C(K \in S C)$. Chứng minh \(HK \bot CD\)
Kẻ $H K \perp S C(K \in S C)$.
Ta có:
\(\left\{ {\begin{array}{*{20}{l}}{SH \bot CD}\\{CH \bot CD}\end{array}} \right.\)\( \Rightarrow CD \bot (SHC)\)\( \Rightarrow HK \bot CD\)\( \Rightarrow HK \bot (SCD)\)
Bước 4: Tính \(d\left( {B,\left( {SCD} \right)} \right)\)
\( \Rightarrow d(H,(SCD)) = HK\)\( = \dfrac{{SH.HC}}{{\sqrt {S{H^2} + H{C^2}} }}\)\( = \dfrac{{2a\sqrt {21} }}{{21}}\)
Mà \(\dfrac{{d(H,(SCD))}}{{d(B,(SCD))}} = \dfrac{{HD}}{{BD}} = \dfrac{2}{3}\)\( \Rightarrow {d{(B,(SCD))}} = \dfrac{{a\sqrt {21} }}{7}\)
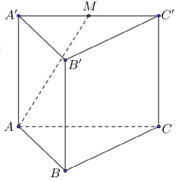
Cho hình lăng trụ tam giác đều \(ABC.A'B'C'\) có độ dài cạnh đáy \(AB = 8,\) cạnh bên bằng \(\sqrt 6 \) (minh họa như hình vẽ). Gọi \(M\) là trung điểm của cạnh \(A'C'\). Khoảng cách từ \(B'\) đến mặt phẳng \(\left( {ABM} \right)\) bằng bao nhiêu?
Đáp án: $d\left(B^{\prime},(A B M)\right)$
Đáp án: $d\left(B^{\prime},(A B M)\right)$
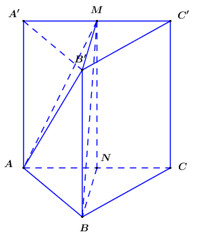
Bước 1: Gọi \(N\) là trung điểm của \(AC\), chứng minh \(d\left( {A;\left( {BB'M} \right)} \right) = d\left( {A;\left( {BB'MN} \right)} \right) = AN\).
Gọi \(N\) là trung điểm của \(AC\) ta có \(\left( {BB'M} \right) \equiv \left( {BB'MN} \right)\) nên \(d\left( {A;\left( {BB'M} \right)} \right) = d\left( {A;\left( {BB'MN} \right)} \right)\).
Vì tam giác ABC đều nên \(AN \bot BN\). Ta có \(\left\{ \begin{array}{l}AN \bot BN\\AN \bot MN\end{array} \right. \Rightarrow AN \bot \left( {BB'MN} \right)\) nên \(d\left( {A;\left( {BB'MN} \right)} \right) = AN = 4\)
Bước 2: Tính \({V_{A.BB'M}} = \dfrac{1}{3}d\left( {A;\left( {BB'MN} \right)} \right).{S_{\Delta BB'M}} = {V_{B'.ABM}}\).
Ta lại có \(BN = \dfrac{{AB\sqrt 3 }}{2} = 4\sqrt 3 ,\,\,MN = AA' = \sqrt 6 \) nên \({S_{BB'MN}} = MN.BN = \sqrt 6 .4\sqrt 3 = 12\sqrt 2 \) \( \Rightarrow {S_{\Delta BB'M}} = 6\sqrt 2 \).
\( \Rightarrow {V_{A.BB'M}} = \dfrac{1}{3}d\left( {A;\left( {BB'MN} \right)} \right).{S_{\Delta BB'M}} = \dfrac{1}{3}.4.12\sqrt 2 = 16\sqrt 2 = {V_{B'.ABM}}\)
Bước 3: Sử dụng \(d\left( {B';\left( {ABM} \right)} \right) = \dfrac{{3{V_{B'.ABM}}}}{{{S_{\Delta ABM}}}}\).
Lại có \({V_{B'.ABM}} = \dfrac{1}{3}d\left( {B';\left( {ABM} \right)} \right).{S_{\Delta ABM}}\) nên \(d\left( {B';\left( {ABM} \right)} \right) \)\(= \dfrac{{3{V_{B'.ABM}}}}{{{S_{\Delta ABM}}}}\).
Ta có:
\(\begin{array}{l}AM = \sqrt {A'{A^2} + A'{M^2}} \\= \sqrt {{{\left( {\sqrt 6 } \right)}^2} + {4^2}} = \sqrt {22} \\AB = 8\\BM = \sqrt {BB{'^2} + B'{M^2}} \\= \sqrt {{{\left( {\sqrt 6 } \right)}^2} + {{\left( {4\sqrt 3 } \right)}^2}} = 3\sqrt 6 \end{array}\)
Bước 4: Sử dụng công thức \({S_{\Delta ABM}} = \sqrt {p\left( {p - AM} \right)\left( {p - AB} \right)\left( {p - BM} \right)} \) với \(p\) là nửa chu vi tam giác \(ABM\).
Gọi \(p\) là nửa chu vi tam giác ABM ta có \(p = \dfrac{{\sqrt {22} + 8 + 3\sqrt 6 }}{2}\).
\( \Rightarrow {S_{\Delta ABM}} \)\(= \sqrt {p\left( {p - AM} \right)\left( {p - AB} \right)\left( {p - BM} \right)} \)\( = 12\sqrt 2 \)
Vậy \(d\left( {B';\left( {ABM} \right)} \right) = \dfrac{{3{V_{B'.ABM}}}}{{{S_{\Delta ABM}}}} = \dfrac{{3.16\sqrt 2 }}{{12\sqrt 2 }} = 4\).

