Câu hỏi:
2 năm trước
Cho hình chóp $S . A B C D$ có đáy $A B C D$ là hình thoi cạnh $a .$ Tam giác $A B C$ đều, hình chiếu vuông góc $H$ của đỉnh $S$ trên mặt phẳng $(A B C D)$ trùng với trọng tâm của tam giác $A B C$. Đường thẳng $S D$ hợp với mặt phẳng $(A B C D)$ một góc $30^{\circ}$. Tính khoảng cách $d$ từ $B$ đến mặt phẳng $(S C D)$ theo $a$
Trả lời bởi giáo viên
Đáp án đúng:
$d=\dfrac{ a \sqrt{21}}{7}$
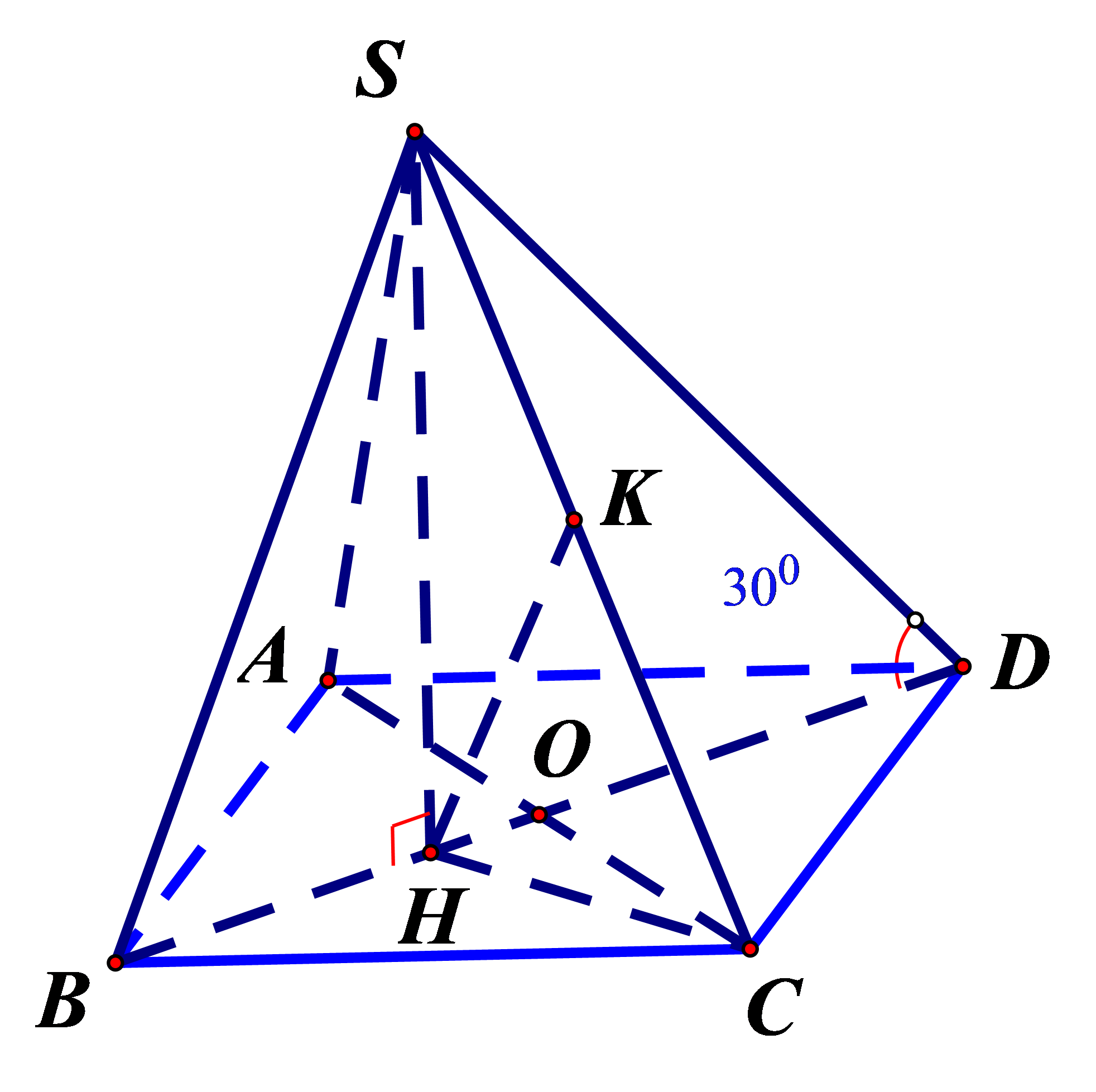
Bước 1: Gọi $O=A C \cap B D$. Tính BO, CH, HD theo a.
Gọi $O=A C \cap B D$
Ta có $\Delta A B C$ dều cạnh $a$ có $H$ là trọng tâm $\Rightarrow B O=\dfrac{a \sqrt{3}}{2}, C H=\dfrac{a \sqrt{3}}{3}, H D=\dfrac{4}{3} B O=\dfrac{2 a \sqrt{3}}{3}$
Bước 2: Tính SH theo a.
Mặt khác, $(\widehat{S D,(A B C D)})=\widehat{S D H}=30^{\circ}$
$\Rightarrow S H=H D \cdot \tan \widehat{S D H}=\dfrac{2 a}{3}$
Lại có $C H \perp A B \Rightarrow C H \perp C D$
Bước 3: Kẻ $H K \perp S C(K \in S C)$. Chứng minh \(HK \bot CD\)
Kẻ $H K \perp S C(K \in S C)$.
Ta có:
\(\left\{ {\begin{array}{*{20}{l}}{SH \bot CD}\\{CH \bot CD}\end{array}} \right.\)\( \Rightarrow CD \bot (SHC)\)\( \Rightarrow HK \bot CD\)\( \Rightarrow HK \bot (SCD)\)
Bước 4: Tính \(d\left( {B,\left( {SCD} \right)} \right)\)
\( \Rightarrow d(H,(SCD)) = HK\)\( = \dfrac{{SH.HC}}{{\sqrt {S{H^2} + H{C^2}} }}\)\( = \dfrac{{2a\sqrt {21} }}{{21}}\)
Mà \(\dfrac{{d(H,(SCD))}}{{d(B,(SCD))}} = \dfrac{{HD}}{{BD}} = \dfrac{2}{3}\)\( \Rightarrow {d{(B,(SCD))}} = \dfrac{{a\sqrt {21} }}{7}\)
Hướng dẫn giải:
Bước 1: Gọi $O=A C \cap B D$. Tính BO, CH, HD theo a.
Bước 2: Tính SH theo a.
Bước 3: Kẻ $H K \perp S C(K \in S C)$. Chứng minh \(HK \bot CD\)
Bước 4: Tính \(d\left( {B,\left( {SCD} \right)} \right)\)
