Hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) xác định trên:
Hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) xác định trên \(\left( {0; + \infty } \right)\).
Hàm số \(y = {\log _a}x\) có đạo hàm là:
Điều kiện xác định: $x>0$
Đạo hàm hàm số \(y = {\log _a}x\) là \(y' = \dfrac{1}{{x\ln a}}\)
Chọn mệnh đề đúng:
Giới hạn cần nhớ: \(\mathop {\lim }\limits_{x \to 0} \dfrac{{\ln \left( {1 + x} \right)}}{x} = 1\)
Cho hàm số \(y = {\log _a}x\). Nếu \(0 < a < 1\) thì hàm số:
Hàm số \(y = {\log _a}x\) nghịch biến trên \(\left( {0; + \infty } \right)\) nếu \(0 < a < 1\) và đồng biến trên \(\left( {0; + \infty } \right)\) nếu \(a > 1\).
Tiệm cận đứng của đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) là đường thẳng:
Đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) có đường tiệm cận đứng là \(x = 0\) (trục \(Oy\))
Điểm \(\left( {{x_0};{y_0}} \right)\) thuộc đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) nếu:
Điểm \(\left( {{x_0};{y_0}} \right)\) thuộc đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\) nếu \({y_0} = {\log _a}{x_0}\).
Điểm nào sau đây không thuộc đồ thị hàm số \(y = {\log _a}x\left( {0 < a \ne 1} \right)\)?
- Đồ thị hàm số luôn đi qua các điểm \(\left( {1;0} \right)\) và \(\left( {a;1} \right)\).
- Với \(x = {a^2}\) thì \(y = {\log _a}x = {\log _a}{a^2} = 2\) nên đồ thị hàm số đi qua \(\left( {{a^2};2} \right)\) nên C sai, D đúng.
Cho hàm số \(y = {\log _{\frac{\pi }{4}}}x\). Khẳng định nào sau đây sai?
- Hàm số \(y = {\log _{\frac{\pi }{4}}}x\) có tập xác định \(D = \left( {0; + \infty } \right)\).
- Vì \(0 < \dfrac{\pi }{4} < 1\) nên hàm số nghịch biến trên TXĐ
- Tiệm cận đứng của đồ thị hàm số là trục $Oy$
- Đồ thị hàm số nằm hoàn toàn bên phải trục hoành (vì \(x > 0\))
Gọi $(C)$ là đồ thị hàm số \(y = \log x\). Tìm khẳng định đúng?
- Đồ thị hàm số \(y = \log x\) nhận trục tung là tiệm cận đứng.
- Đồ thị hàm số không có tiệm cận ngang và cắt trục hoành tại điểm $(1;0)$ nên các đáp án B,C,D đều sai
Trong các khẳng định sau, khẳng định nào đúng?
\(\log a + \log b = \log \left( {ab} \right)\) nên ý A sai
Nhận thấy \({a^{x + y}} = {a^x}.{a^y}\) nên mệnh đề ở ý B sai.
Vì $12 > 1$ nên \(y = {\log _{12}}x\) là hàm đồng biến trên khoảng $(0; + \infty )$ nên D sai
Cho $a, b$ là các số thực, thỏa mãn \(0 < a < 1 < b\), khẳng định nào sau đây là đúng?
Ta có: \(0 < a < 1\) nên hàm số \(y = {\log _a}x\) nghịch biến, do đó \(b > 1\) nên \({\log _a}b < {\log _a}1 = 0\).
Vì \(b > 1\) nên hàm số \(y = {\log _b}x\) đồng biến, do đó \(a < 1\) nên \({\log _b}a < {\log _b}1 = 0\).
Vậy \({\log _a}b < 0;{\log _b}a < 0 \Rightarrow {\log _a}b + {\log _b}a < 0\).
Cho \(a > 0,a \ne 1\). Tìm mệnh đề đúng trong các mệnh đề sau:
Cho \(a > 0;a \ne 1\) khi đó hàm số \(y = {a^x}\) có tập xác định là \(R\) , tập giá trị là \(\left( {0; + \infty } \right)\)
Hàm số \(y = {\log _a}x\) có tập xác định là \(\left( {0; + \infty } \right)\) , tập giá trị là \(R\)
Suy ra B đúng
Tìm tập xác định D của hàm số \(y = {\log _{\sqrt 2 }}\left( {\dfrac{{ - 3}}{{2 - 2x}}} \right)\).
Điều kiện : \(\dfrac{{ - 3}}{{2 - 2x}} > 0 \Leftrightarrow 2 - 2x < 0 \Leftrightarrow x > 1.\)
Đạo hàm hàm số \(y = {\log _{2018}}\left( {2018x + 1} \right)\) là:
Ta có: \(\left[ {{{\log }_{2018}}\left( {2018x + 1} \right)} \right]' = \dfrac{{\left( {2018x + 1} \right)'}}{{\left( {2018x + 1} \right)\ln 2018}} = \dfrac{{2018}}{{\left( {2018x + 1} \right)\ln 2018}}\)
Tính đạo hàm hàm số \(y = \ln \left( {1 + \sqrt {x + 1} } \right)\).
Ta có: \(y' = \left[ {\ln \left( {1 + \sqrt {x + 1} } \right)} \right]' = \dfrac{{\left( {1 + \sqrt {x + 1} } \right)'}}{{1 + \sqrt {x + 1} }} = \dfrac{{\dfrac{1}{{2\sqrt {x + 1} }}}}{{1 + \sqrt {x + 1} }} = \dfrac{1}{{2\sqrt {x + 1} \left( {1 + \sqrt {x + 1} } \right)}}\)
Cho $a, b$ là các số thực dương, thỏa mãn \({a^{\frac{3}{4}}} > {a^{\frac{4}{5}}}\) và \({\log _b}\dfrac{1}{2} < {\log _b}\dfrac{2}{3}\). Mệnh đề nào dưới đây đúng?
Ta có:
\(\dfrac{3}{4} < \dfrac{4}{5}\) và \({a^{\frac{3}{4}}} > {a^{\frac{4}{5}}}\)\( \Rightarrow 0 < a < 1\)
\(\dfrac{1}{2} < \dfrac{2}{3}\) và \({\log _b}\dfrac{1}{2} < {\log _b}\dfrac{2}{3}\)\( \Rightarrow b > 1\)
Hàm số nào trong các hàm số sau có đồ thị phù hợp với hình vẽ bên?
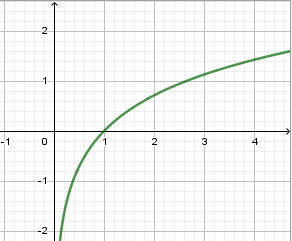
Đồ thị hàm số đã cho có $y \to -\infty $ khi $x \to {0^ + }$ nên nó là đồ thị hàm số $y = lo{g_a}x$ với $a > 1$
Nếu gọi \(({G_1})\) là đồ thị hàm số \(y = {a^x}\) và \(({G_2})\)là đồ thị hàm số \(y = {\log _a}x\) với \(0 < a \ne 1\). Mệnh đề nào dưới đây đúng ?
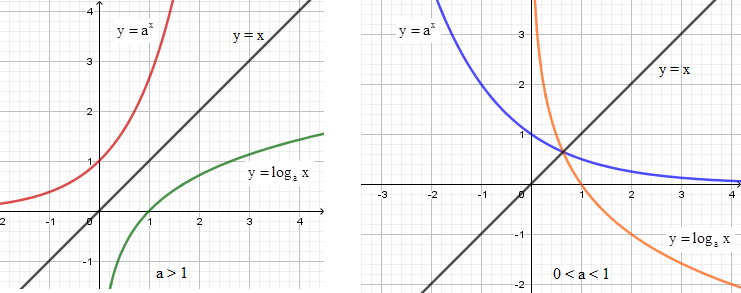
Quan sát hình vẽ ta thấy hai đồ thị hàm số đối xứng nhau qua đường thẳng \(y = x\).
Cho ba số thực dương $a, b, c$ khác $1$. Đồ thị các hàm số $y = \log_{a} x, y=\log_{b} x, y= \log_{c} x$ được cho trong hình vẽ sau:
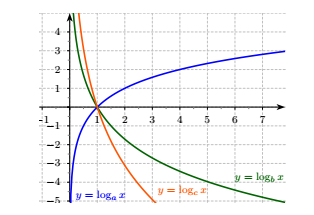
Mệnh đề nào dưới đây đúng?
Quan sát hình vẽ ta thấy:
- Hàm số \(y = {\log _a}x\) là hàm đồng biến nên ta có \(a > 1\) .
- Hai hàm số \(y = {\log _b}x,y = {\log _c}x\) nghịch biến nên có \(0 < b,c < 1\)
Từ nhận xét này ta thấy \(a\) là số lớn nhất.
Tìm tất cả các giá trị thực của tham số $m$ sao cho hàm số \(y = \log ({x^2} - 2mx + 4)\) có tập xác định là $R$
Giải điều kiện: \({x^2} - 2mx + 4 > 0,\forall x \in R\)
\(\Delta ' = {m^2} - 4 < 0 \Leftrightarrow (m - 2)(m + 2) < 0\). Suy ra \( - 2 < m < 2\)

