Cho tứ diện \(ABCD\) có \(AB\) vuông góc với \(CD\), \(AB = CD = 6\). \(M\) là điểm thuộc cạnh \(BC\) sao cho \(MC = x.BC{\rm{ }}\left( {0 < x < 1} \right)\). Mặt phẳng\(\left( P \right)\) song song với \(AB\) và \(CD\) lần lượt cắt \(BC,DB,AD,AC\) tại \(M,N,P,Q\). Diện tích lớn nhất của tứ giác bằng bao nhiêu?
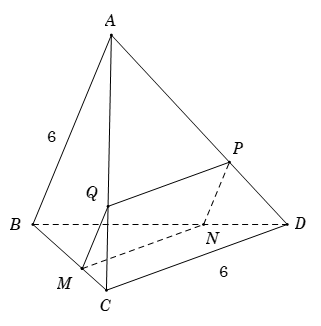
Xét tứ giác \(MNPQ\) có \(\left\{ \begin{array}{l}MQ{\rm{//}}NP{\rm{//}}AB\\MN{\rm{//}}PQ{\rm{//}}CD\end{array} \right.\)\( \Rightarrow MNPQ\) là hình bình hành.
Mặt khác, \(AB \bot CD \Rightarrow MQ \bot MN\). Do đó, \(MNPQ\) là hình chữ nhật.
Vì \(MQ{\rm{//}}AB\) nên \(\dfrac{{MQ}}{{AB}} = \dfrac{{CM}}{{CB}} = x \Rightarrow MQ = x.AB = 6x\).
Theo giả thiết \(MC = x.BC \Rightarrow BM = \left( {1 - x} \right)BC\).
Vì \(MN{\rm{//}}CD\) nên \(\dfrac{{MN}}{{CD}} = \dfrac{{BM}}{{BC}} = 1 - x \Rightarrow MN = \left( {1 - x} \right).CD = 6\left( {1 - x} \right)\).
Diện tích hình chữ nhật \(MNPQ\) là
\({S_{MNPQ}} = MN.MQ = 6\left( {1 - x} \right).6x = 36.x.\left( {1 - x} \right) \le 36{\left( {\dfrac{{x + 1 - x}}{2}} \right)^2} = 9\) .
Ta có \({S_{MNPQ}} = 9\) khi \(x = 1 - x \Leftrightarrow x = \dfrac{1}{2}\) .
Vậy diện tích tứ giác \(MNPQ\) lớn nhất bằng \(9\) khi \(M\) là trung điểm của \(BC\).
Cho hình chóp S.ABCD có đáy ABCD là hình vuông cạnh bằng a. Hình chiếu vuông góc của S trên mặt phẳng (ABCD) trùng với trung điểm H của cạnh AB. Biết tam giác SAB là tam giác đều. Số đo của góc giữa SA và CD là
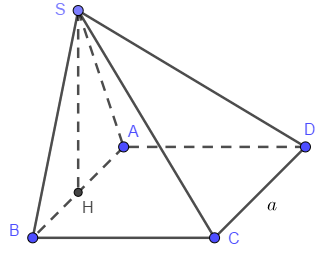
Bước 1:
\(CD||AB \Rightarrow \widehat {\left( {SA,CD} \right)}\)\( = \widehat {\left( {SA,AB} \right)} = \widehat {SAB}\)
Bước 2:
Vì tam giác SAB là tam giác đều.
\( \Rightarrow \widehat {SAB} = 60^\circ \)
Vậy góc giữa SA và CD là \({60^0}\)

