Điểm thuộc đường thẳng d:x−y−1=0 cách đều hai điểm cực trị của đồ thị hàm số y=x3−3x2+2 là
Ta có y=x3−3x2+2→y′=3x2−6x;y′=0⇔[x=0⇒y(0)=2x=2⇒y(2)=−2.
Suy ra tọa độ hai điểm cực trị của đồ thị hàm số là A(0;2),B(2;−2).
Gọi M∈d⇒M(a;a−1), khi đó {MA=√a2+(a−3)2MB=√(a−2)2+(a+1)2
Mà M cách đều A,B
Suy ra MA2=MB2⇔a2+(a−3)2=(a−2)2+(a+1)2⇔a=1⇒M(1;0).
Cho hàm số y=f(x) có đồ thị như hình vẽ bên.
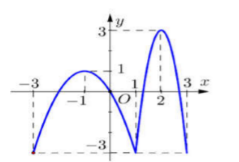
Trên đoạn [−3;3], hàm số đã cho có mấy điểm cực trị?
Dựa vào đồ thị hàm số ta thầy, trên đoạn [−3;3], hàm số y=f(x) có 3 điểm cực trị là (−1;1);(1;−3);(2;3).
Cho hàm số f(x)=ax3+bx2+cx+d (với a,b,c,d∈R và a≠0) có đồ thị như hình vẽ. Số điểm cực trị của hàm số g(x)=f(−2x2+4x) là
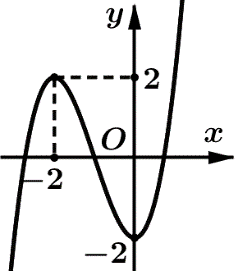
Từ đồ thị ta thấy, hàm số f(x) đạt cực trị tại các điểm x=-2 và x=0 nên f'(-2)=0, f'(0)=0.
Ta có: g′(x)=(−4x+4)f′(−2x2+4x).
Cho g′(x)=0⇔[−4x+4=0f′(−2x2+4x)=0(∗)
Do f′(−2)=0,f′(0)=0
⇒f′(−2x2+4x)=0⇔[−2x2+4x=0−2x2+4x=−2
Do đó,
(∗)⇔[−4x+4=0−2x2+4x=−2−2x2+4x=0⇔[x=1x=1±√2x=0x=2
Các nghiệm này đều là nghiệm đơn.
Do đó g′(x) đổi dấu qua 5 điểm trên.
Vậy hàm số y=g(x) có 5 điểm cực trị.
Cho hàm số y=f(x) có đồ thị f′(x) như hình vẽ. Số điểm cực trị của hàm số y=f(x) là:
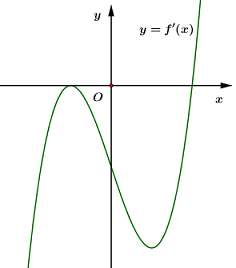
Dựa vào đồ thị hàm số y=f′(x) ta thấy f′(x) có 1 lần đổi dấu từ âm sang dương
⇒ Hàm số y=f(x) có 1 điểm cực trị.
Cho hàm số y=f(x) liên tục trên R và có bảng xét dấu f′(x) như sau :

Hàm số y=f(x) có bao nhiêu điểm cực trị ?
Dựa vào bảng biến thiên ta thấy hàm số đổi dấu khi đi qua 4 điểm có hoành độ là −1;0;2;4.
Vậy hàm số y=f(x) có 4 điểm cực trị.
Cho hàm số f(x) có bảng biến thiên như sau:
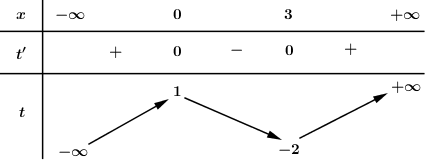
Số điểm cực trị của hàm số f(x2−2x) là:
Đặt g(x)=f(x2−2x) ta có g′(x)=(2x−2)f′(x2−2x).
g′(x)=0⇔[x=1f′(x2−2x)=0.
Dựa vào BBT ta thấy f′(x2−2x)=0⇔[x2−2x=0x2−2x=3⇔[x=0x=2x=−1x=3
⇒ Phương trình g′(x)=0 có 5 nghiệm đơn x=0,x=2,x=3,x=−1,x=1
Vậy hàm số đã cho có 5 điểm cực trị.
Số điểm cực trị của hàm số y=|x2−3x+2| là:
Xét hàm số y=x2−3x+2 ta có: y′=2x−3⇒y′=0 ⇔2x−3=0 ⇔x=32
⇒ Hàm số y=x2−3x+2 có 1 cực trị.
Xét phương trình hoành độ giao điểm của đồ thị hàm số y=x2−3x+2 với trục hoành ta có:
x2−3x+2=0 ⇔(x−1)(x−2)=0⇔[x=1x=2
⇒ Đồ thị hàm số y=x2−3x+2 cắt trục hoành tại 2 điểm phân biệt.
⇒ Số điểm cực trị của hàm số y=|x2−3x+2| là: S=1+2=3 cực trị.
Cho hàm số f(x) có đạo hàm f′(x)=x2(x+2)(x−3). Điểm cực đại của hàm số g(x)=f(x2−2x) là:
Ta có:
g(x)=f(x2−2x)⇒g′(x)=(2x−2)f′(x2−2x)g′(x)=0⇔[2x−2=0f′(x2−2x)=0
⇔[x=1x2−2x=−2x2−2x=3 (ta không xét x2−2x=0 vì x=0 là nghiệm kép của phương trình f′(x)=0).
⇔[x=1x=3x=−1 và qua các nghiệm này thì g′(x) đổi dấu.
Chọn x=4 ta có g′(4)=6f′(8)>0.
Khi đó ta có BXD của g′(x) như sau:
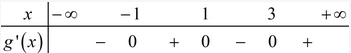
Điểm cực đại của hàm số g(x)=f(x2−2x) là xCD=1.
Hình vẽ dưới đây mô tả số người nhiễm Covid-19 đang được điều trị ở Việt Nam tính từ ngày 23/01/2020 đến ngày 13/02/2021.
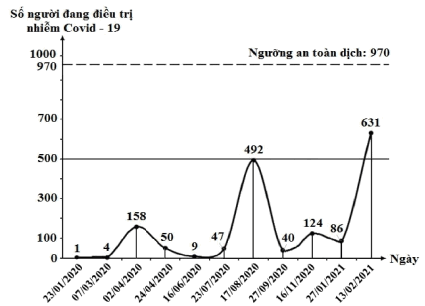
Hỏi từ ngày 16/06/2020 đến ngày 27/01/2021, ngày nào Việt Nam có số người được điều trị Covid-19 nhiều nhất?
Dựa vào hình vẽ ta thấy được, trong khoảng thời gian từ ngày 16/06/2021 đến ngày 27/01/2021, ngày 17/08/2020 có số người được điều trị Covid – 19 nhiều nhất là 492 người.
Cho hàm số f(x) có đạo hàm f′(x)=x(x+2)2(x2−x−2),∀x∈R. Hàm số f(x) có n điểm cực trị. Tìm n.
Đáp án
Đáp án
Bước 1: Tìm nghiệm của f′(x)=0
Ta có: f′(x)=x(x+2)2(x2−x−2)∀x∈R
⇒f′(x)=0⇔x(x+2)2(x2−x−2)=0⇔x(x+2)2(x+1)(x−2)=0⇔[x=0x+2=0x+1=0x−2=0⇔[x=0x=−2x=−1x=2
Bước 2: Xác định số nghiệm bội lẻ của phương trình f′(x)=0.
Trong đó: x=−2 là nghiệm bội 2 nên x=−2 không là điểm cực trị của hàm số y=f(x).
Còn lại: x=0;x=−1;x=2 là các nghiệm bội 1 của hàm số nên chúng là các điểm cực trị của hàm số y=f(x).
Vậy hàm số y=f(x) có 3 điểm cực trị.
Hàm số f(x)=x4(x−1)2 có bao nhiêu điểm cực trị?
Đáp án:
Đáp án:
Bước 1: Tính f′(x).
Ta có:
f(x)=x4(x−1)2⇒f′(x)=4x3(x−1)2+x4.2(x−1)f′(x)=2x3(x−1)[2(x−1)+x]f′(x)=2x3(x−1)(3x−2)
Bước 2: Giải phương trình f′(x)=0 xác định số nghiệm bội lẻ.
f′(x)=0⇔[x=0(nghiemboi3)x=1(nghiemdon)x=23(nghiemdon)
Vậy hàm số f(x) đã cho có 3 điểm cực trị.
Đồ thị hàm số y=x3−2mx2+m2x+n có điểm cực tiểu là A(1;3). Giá trị của m+n bằng:
Đáp án:
Đáp án:
Bước 1: Tìm y' và y''.
Ta có: y=x3−2mx2+m2x+n⇒y′=3x2−4mx+m2,y″.
Bước 2:
Đồ thị hàm số y = {x^3} - 2m{x^2} + {m^2}x + n có điểm cực tiểu là A\left( {1;3} \right) khi và chỉ khi \left\{ \begin{array}{l}f'\left( 1 \right) = 0\\f''\left( 1 \right) > 0\\f\left( 1 \right) = 3\end{array} \right..
\Rightarrow \left\{ \begin{array}{l}3 - 4m + {m^2} = 0\\6 - 4m > 0\\1 - 2m + {m^2} + n = 3\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}\left[ \begin{array}{l}m = 3\\m = 1\end{array} \right.\\m < \dfrac{3}{2}\\n = 3 - {\left( {m - 1} \right)^2}\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m = 1\\n = 3\end{array} \right..
Vậy m + n = 1 + 3 = 4.
Cho hàm số f\left( x \right) có f'\left( x \right) = {x^{2021}}{\left( {x - 1} \right)^{2020}}\left( {x + 1} \right)\forall x \in \mathbb{R}. Hàm số đã cho có bao nhiêu điểm cực trị?
Đáp án:
Đáp án:
Ta có f'\left( x \right) = 0 \Leftrightarrow {x^{2021}}{\left( {x - 1} \right)^{2020}}\left( {x + 1} \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\left( {nghiem\,\,boi\,\,le} \right)\\x = 1\,\,\left( {nghiem\,\,boi\,\,chan} \right)\\x = - 1\,\,\left( {nghiem\,\,boi\,\,le} \right)\end{array} \right.
Vậy hàm số f\left( x \right) có 2 điểm cực trị x = 0,\,\,x = - 1.
Cho hàm số f\left( x \right) có đạo hàm f'\left( x \right) = x\left( {x - 1} \right){\left( {x + 4} \right)^3},\forall x \in \mathbb{R}. Số điểm cực tiểu của hàm số đã cho là:
Đáp án:
Đáp án:
Bảng xét dấu

\Rightarrow Hàm số đã cho có 2 điểm cực tiểu.
Cho hàm số y = f\left( x \right) có đạo hàm f'\left( x \right) = {x^2}\left( {{x^2} - 1} \right). Điểm cực tiểu của hàm số y = f\left( x \right) là:
Đáp án: x=
Đáp án: x=
Bước 1: Giải phương trình f'\left( x \right) = 0.
Ta có:
f'\left( x \right) = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\,\,\left( {nghiem\,\,boi\,\,chan} \right)\\{x^2} - 1 = 0 \Leftrightarrow \left[ \begin{array}{l}x = 1\,\,\,\,\,\left( {nghiem\,\,boi\,\,le} \right)\\x = - 1\,\,\left( {nghiem\,\,boi\,\,le} \right)\end{array} \right.\end{array} \right.
Bước 2: Lập BBT của hàm số từ đó xác định điểm cực tiểu của hàm số.
BBT:
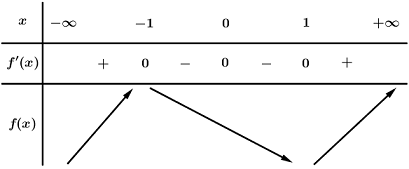
Vậy điểm cực tiểu của hàm số là x = 1.

