Các dạng toán viết phương trình mặt phẳng

Gọi $\overrightarrow {{n_{\left( \alpha  \right)}}}  = \left( {a;b;c} \right)$ là 1 VTPT của $\left( \alpha  \right)$.

Ta có $\overrightarrow {{n_{\left( {Oyz} \right)}}}  = \left( {1;0;0} \right)$ nên góc giữa $\left( \alpha  \right)$ và $\left( {Oyz} \right)$ bằng ${60^0}$

$\begin{array}{l} \Leftrightarrow \cos {60^0} = \dfrac{{\left| {\overrightarrow {{n_{\left( \alpha  \right)}}} .\overrightarrow {{n_{\left( {Oyz} \right)}}} } \right|}}{{\left| {\overrightarrow {{n_{\left( \alpha  \right)}}} } \right|.\left| {\overrightarrow {{n_{\left( {Oyz} \right)}}} } \right|}}\\ \Leftrightarrow \dfrac{1}{2} = \dfrac{{\left| {a.1 + b.0 + c.0} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} .\sqrt {{1^2} + {0^2} + {0^2}} }}\\ \Leftrightarrow \dfrac{1}{2} = \dfrac{{\left| a \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}\end{array}$

$\left( \alpha  \right)$ đi qua $M\left( {4;0;0} \right)$ và nhận $\overrightarrow {{n_{\left( \alpha  \right)}}}  = \left( {a;b;c} \right)$ làm VTPT nên $\left( \alpha  \right)$ có phương trình tổng quát là:

$a\left( {x - 4} \right) + b\left( {y - 0} \right) + c\left( {z - 0} \right) = 0$$\Leftrightarrow ax + by + cz - 4a = 0$

Suy ra khoảng cách từ O đến $\left( \alpha  \right)$ là:

$d\left( {O,\left( \alpha  \right)} \right) = \dfrac{{\left| {a.0 + b.0 + c.0 - 4a} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }}$$= \dfrac{{\left| {4a} \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }} = 4.\dfrac{{\left| a \right|}}{{\sqrt {{a^2} + {b^2} + {c^2}} }} = 4.\dfrac{1}{2} = 2$

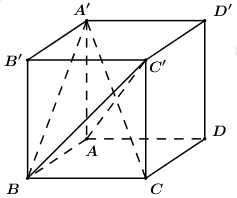
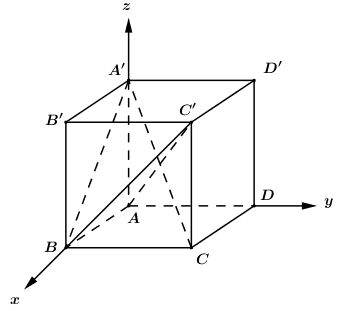
Gắn hệ trục tọa độ như hình vẽ, coi hình lập phương có cạnh bằng 1 ta có:

$A\left( {0;0;0} \right)$, $B\left( {1;0;0} \right)$, $C\left( {1;1;0} \right)$, $A'\left( {0;0;1} \right)$, $C'\left( {1;1;1} \right)$.

Ta có: $\overrightarrow {A'B}  = \left( {1;0; - 1} \right),\,\,\overrightarrow {BC}  = \left( {0;1;0} \right)$ $\Rightarrow \left[ {\overrightarrow {A'B} ;\overrightarrow {BC} } \right] = \left( {1;0;1} \right)$ $\Rightarrow \left( {A'BC} \right)$ có 1 VTPT là $\overrightarrow {{n_1}}  = \left( {1;0;1} \right)$.

$\overrightarrow {AB}  = \left( {1;0;0} \right),\,\,\overrightarrow {AC'}  = \left( {1;1;1} \right)$ $\Rightarrow \left[ {\overrightarrow {AB} ;\overrightarrow {AC'} } \right] = \left( {0; - 1;1} \right)$ $\Rightarrow \left( {ABC'} \right)$ có 1 VTPT là $\overrightarrow {{n_2}}  = \left( {0; - 1;1} \right)$.

Gọi $\alpha$ là góc giữa hai mặt phẳng $\left( {A'BC} \right)$ và $\left( {ABC'} \right)$ ta có:

$\cos \alpha  = \dfrac{{\left| {\overrightarrow {{n_1}} .\overrightarrow {{n_2}} } \right|}}{{\left| {\overrightarrow {{n_1}} } \right|.\left| {\overrightarrow {{n_2}} } \right|}} = \dfrac{{\left| {1.0 + 0.\left( { - 1} \right) + 1.1} \right|}}{{\sqrt {{1^2} + {0^2} + {1^2}} .\sqrt {{0^2} + {{\left( { - 1} \right)}^2} + {1^2}} }} = \dfrac{1}{2}$.

Ta có: $\left( P \right):\,\,\,4x - 4y + 2z - 7 = 0$ có VTPT là: $\overrightarrow {{n_P}}  = \left( {4; - 4;\,\,2} \right) = 2\left( {2; - 2;\,\,1} \right)$

$\left( Q \right):\,\,\,2x - 2y + z + 4 = 0$ có VTPT là: $\overrightarrow {{n_Q}}  = \left( {2; - 2;\,\,1} \right)$

$\Rightarrow \overrightarrow {{n_P}} //\overrightarrow {{n_Q}}  \Rightarrow \left( P \right)//\left( Q \right)$

Lấy điểm $A\left( {0;\,\,2;\,\,0} \right) \in \left( Q \right)$

$\Rightarrow d\left( {\left( P \right);\,\,\left( Q \right)} \right) = d\left( {A;\,\,\left( P \right)} \right)$ $= \dfrac{{\left| {4.0 - 4.2 + 2.0 - 7} \right|}}{{\sqrt {{4^2} + {{\left( { - 4} \right)}^2} + {2^2}} }} = \dfrac{{15}}{6} = \dfrac{5}{2}$

Mà hai mặt phẳng $\left( P \right),\,\,\,\left( Q \right)$  chứa hai mặt của hình lập phương đã cho

$\Rightarrow$ Độ dài cạnh của hình lập phương là $d\left( {\left( P \right);\,\,\left( Q \right)} \right) = \dfrac{5}{2}.$

$\Rightarrow V = {\left( {\dfrac{5}{2}} \right)^3} = \dfrac{{125}}{8}.$

Bước 1: Tìm VTPT của (P), (Q), (R)

+) $(P): x+y+z-1=0$ có VTPT $\vec{a}=(1 ; 1 ; 1)$

+) $(Q): 2 x+m y+2 z+3=0$ có VTPT $\vec{b}=(2 ; m ; 2)$

+) $(R):-x+2 y+n z=0$ có VTPT $\vec{c}=(-1 ; 2 ; n)$

Bước 2: Tính $m+2 n$

  $(P)\perp(R)$$\Leftrightarrow \vec{d} \cdot \vec{c}=0 \Leftrightarrow n=-1$

$(P) / /(Q) \Leftrightarrow \dfrac{2}{1}=\dfrac{m}{1}=\dfrac{2}{1} \Leftrightarrow m=2$

Vây $m+2 n=2+2(-1)=0$