Sử dụng phương pháp đổi biến số để tính tích phân
Kỳ thi ĐGNL ĐHQG Hà Nội
Cho tích phân \(I = \int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{6\tan x}}{{{{\cos }^2}x\sqrt {3\tan x + 1} }}dx} \). Giả sử đặt \(u = \sqrt {3\tan x + 1} \) thì ta được:
Đặt \(u = \sqrt {3\tan x + 1} \Rightarrow {u^2} = 3\tan x + 1 \Leftrightarrow 2udu = \dfrac{3}{{{{\cos }^2}x}}dx \Rightarrow \dfrac{{dx}}{{{{\cos }^2}x}} = \dfrac{{2udu}}{3}\)
Và \(\tan x = \dfrac{{{u^2} - 1}}{3}\)
Đổi cận: \(\left\{ \begin{array}{l}x = 0 \Rightarrow u = 1\\x = \dfrac{\pi }{4} \Rightarrow u = 2\end{array} \right.\)
Khi đó ta có: \(I = \int\limits_0^{\dfrac{\pi }{4}} {\dfrac{{6\tan x}}{{{{\cos }^2}x\sqrt {3\tan x + 1} }}dx} \Rightarrow I = \int\limits_1^2 {\dfrac{{2\left( {{u^2} - 1} \right)2udu}}{{3u}}} = \dfrac{4}{3}\int\limits_1^2 {\left( {{u^2} - 1} \right)du} \)
Tính tích phân \(I = \int\limits_0^{\dfrac{\pi }{2}} {{{\left( {1 - \cos x} \right)}^n}\sin xdx} \) bằng:
Đặt \(t = 1 - \cos x \Rightarrow dt = \sin xdx\)
Đổi cận: \(\left\{ \begin{array}{l}x = 0 \Rightarrow t = 0\\x = \dfrac{\pi }{2} \Rightarrow t = 1\end{array} \right.\)
Khi đó \(I = \int\limits_0^1 {{t^n}dt} = \left. {\dfrac{{{t^{n + 1}}}}{{n + 1}}} \right|_0^1 = \dfrac{1}{{n + 1}}\)
Biết \(\int\limits_0^{\dfrac{\pi }{2}} {\dfrac{{3\sin x + \cos x}}{{2\sin x + 3\cos x}}dx = - \dfrac{7}{{13}}\ln 2 + b\ln 3 + c\pi \,\,\left( {b,c \in \mathbb{Q}} \right).} \) Tính \(\dfrac{b}{c}.\)
Ta có \(3\sin x + \cos x = A\left( {2\sin x + 3\cos x} \right) + B\left( {2\cos x - 3\sin x} \right)\)
\(\begin{array}{l} \Leftrightarrow 3\sin x + \cos x = \left( {2A - 3B} \right)\sin x + \left( {3A + 2B} \right)\cos x\\ \Leftrightarrow \left\{ \begin{array}{l}2A - 3B = 3\\3A + 2B = 1\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}A = \dfrac{9}{{13}}\\B = - \dfrac{7}{{13}}\end{array} \right.\end{array}\)
Nên \(3\sin x + \cos x = \dfrac{9}{{13}}\left( {2\sin x + 3\cos x} \right) - \dfrac{7}{{13}}\left( {2\cos x - 3\sin x} \right)\)
Từ đó ta có
\(\begin{array}{l}\int\limits_0^{\dfrac{\pi }{2}} {\dfrac{{3\sin x + \cos x}}{{2\sin x + 3\cos x}}dx = } \int\limits_0^{\dfrac{\pi }{2}} {\dfrac{{\dfrac{9}{{13}}\left( {2\sin x + 3\cos x} \right) - \dfrac{7}{{13}}\left( {2\cos x - 3\sin x} \right)}}{{2\sin x + 3\cos x}}dx = } \\ = \dfrac{9}{{13}}\int\limits_0^{\dfrac{\pi }{2}} {dx} - \dfrac{7}{{13}}\int\limits_0^{\dfrac{\pi }{2}} {\dfrac{{2\cos x - 3\sin x}}{{2\sin x + 3\cos x}}dx} \\ = \dfrac{{9\pi }}{{26}} - \dfrac{7}{{13}}\int\limits_0^{\dfrac{\pi }{2}} {\dfrac{1}{{2\sin x + 3\cos x}}d\left( {2\sin x + 3\cos x} \right)} \\ = \dfrac{{9\pi }}{{26}} - \dfrac{7}{{13}}\left. {\ln \left| {2\sin x + 3\cos x} \right|} \right|_0^{\dfrac{\pi }{2}}\\ = \dfrac{{9\pi }}{{26}} - \dfrac{7}{{13}}\ln 2 + \dfrac{7}{{13}}\ln 3\end{array}\)
Suy ra \(b = \dfrac{7}{{13}};c = \dfrac{9}{{26}} \Rightarrow \dfrac{b}{c} = \dfrac{{14}}{9}\).
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và có \(\int_0^1 {f\left( x \right)dx = 3\int_0^3 {f\left( x \right)} dx = 6} \). Giá trị của \(\int_{ - 1}^1 {f\left( {\left| {2x - 1} \right|} \right)dx} \) bằng:
Ta có \(\int\limits_{ - 1}^1 {f\left( {\left| {2x - 1} \right|} \right)dx} = \int\limits_{ - 1}^{\frac{1}{2}} {f\left( {1 - 2x} \right)dx} + \int\limits_{\frac{1}{2}}^1 {f\left( {2x - 1} \right)dx} \)
\( \Rightarrow I = - \frac{1}{2}\int\limits_{ - 1}^{\frac{1}{2}} {f\left( {1 - 2x} \right)d\left( {1 - 2x} \right)} + \frac{1}{2}\int\limits_{\frac{1}{2}}^1 {f\left( {2x - 1} \right)d\left( {2x - 1} \right)} \)
\(\begin{array}{l} \Leftrightarrow I = - \frac{1}{2}\int\limits_3^0 {f\left( t \right)dt} + \frac{1}{2}\int\limits_0^1 {f\left( t \right)dt} \\ \Leftrightarrow I = \frac{1}{2}\int\limits_0^3 {f\left( t \right)dt} + \frac{1}{2}\int\limits_0^1 {f\left( t \right)dt} = \frac{1}{2}\left( {2 + 6} \right) = 4\end{array}\)
Cho \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) thỏa mãn \(f\left( x \right) = f\left( {2020 - x} \right)\) và \(\int\limits_3^{2017} {f\left( x \right)dx} = 4\). Khi đó \(\int\limits_3^{2017} {xf\left( x \right)dx} \) bằng:
Xét tích phân \(\int\limits_3^{2017} {xf\left( x \right)dx} \).
Đặt \(x = 2020 - t \Rightarrow dx = - dt\).
Đổi cận: \(\left\{ \begin{array}{l}x = 3 \Rightarrow t = 2017\\x = 2017 \Rightarrow t = 3\end{array} \right.\) , khi đó ta có:
\(\begin{array}{l}\int\limits_3^{2017} {xf\left( x \right)dx} = - \int\limits_{2017}^3 {\left( {2020 - t} \right)f\left( {2020 - t} \right)dt} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \int\limits_3^{2017} {\left( {2020 - x} \right)f\left( {2020 - x} \right)dx} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = \int\limits_3^{2017} {\left( {2020 - x} \right)f\left( x \right)dx} \\\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, = 2020\int\limits_3^{2017} {f\left( x \right)dx} - \int\limits_3^{2017} {xf\left( x \right)dx} \\ \Leftrightarrow 2\int\limits_3^{2017} {xf\left( x \right)dx} = 2020\int\limits_3^{2017} {f\left( x \right)dx} \\ \Leftrightarrow \int\limits_3^{2017} {xf\left( x \right)dx} = 1010.4\\ \Leftrightarrow \int\limits_3^{2017} {xf\left( x \right)dx} = 4040\end{array}\)
Cho hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) và \(\int\limits_1^9 {\dfrac{{f\left( {\sqrt x } \right)}}{{\sqrt x }}{\rm{d}}x = 4} ,\)\(\int\limits_0^{\dfrac{\pi }{2}} {f\left( {\sin x} \right)\cos x{\rm{d}}x = 2} .\) Tính tích phân \(I = \int\limits_0^3 {f\left( x \right){\rm{d}}x} .\)
Xét tích phân \(\int\limits_1^9 {\dfrac{{f\left( {\sqrt x } \right)}}{{\sqrt x }}{\rm{d}}x = 4} \).
Đặt \(t = \sqrt x \Rightarrow {t^2} = x \Rightarrow 2tdt = dx\).
Đổi cận: \(\left\{ \begin{array}{l}x = 1 \Rightarrow t = 1\\x = 9 \Rightarrow t = 3\end{array} \right.\).
Khi đó ta có: \(\int\limits_1^9 {\dfrac{{f\left( {\sqrt x } \right)}}{{\sqrt x }}{\rm{d}}x} = \int\limits_1^3 {\dfrac{{f\left( t \right)2tdt}}{t}} = 2\int\limits_1^3 {f\left( t \right)dt} = 2\int\limits_1^3 {f\left( x \right)dx} \).
\( \Rightarrow 2\int\limits_1^3 {f\left( x \right)dx} = 4 \Leftrightarrow \int\limits_1^3 {f\left( x \right)dx} = 2\).
Xét tích phân \(\int\limits_0^{\dfrac{\pi }{2}} {f\left( {\sin x} \right)\cos x{\rm{d}}x = 2} \).
Đặt \(u = \sin x \Rightarrow du = \cos xdx\).
Đổi cận: \(\left\{ \begin{array}{l}x = 0 \Rightarrow u = 0\\x = \dfrac{\pi }{2} \Rightarrow u = 1\end{array} \right.\).
Khi đó ta có: \(\int\limits_0^{\dfrac{\pi }{2}} {f\left( {\sin x} \right)\cos x{\rm{d}}x} = \int\limits_0^1 {f\left( u \right)du} = \int\limits_0^1 {f\left( x \right)dx} = 2\).
Vậy \(I = \int\limits_0^3 {f\left( x \right){\rm{d}}x} = \int\limits_0^1 {f\left( x \right){\rm{d}}x} + \int\limits_1^3 {f\left( x \right){\rm{d}}x} = 2 + 2 = 4\).
Cho \(\int\limits_0^1 {f\left( x \right)dx = 1.} \) Tính \(\int\limits_0^{\frac{\pi }{4}} {\left( {2{{\sin }^2}x - 1} \right)f\left( {\sin 2x} \right)dx.} \)
Đặt \(t = \sin 2x \Rightarrow dt = 2\cos 2xdx\) \( \Rightarrow - \dfrac{1}{2}dt = \left( {2{{\sin }^2}x - 1} \right)dx\)
Đổi cận: \(\left\{ \begin{array}{l}x = 0 \Rightarrow t = 0\\x = \dfrac{\pi }{4} \Rightarrow t = 1\end{array} \right..\)
\( \Rightarrow I = \int\limits_0^{\frac{\pi }{4}} {\left( {2{{\sin }^2}x - 1} \right)f\left( {\sin 2x} \right)dx} \)\( = - \dfrac{1}{2}\int\limits_0^1 {f\left( t \right)dt} = - \dfrac{1}{2}.1 = - \dfrac{1}{2}.\)
Cho hàm số \(f(x)\) liên tục trên \(\left[ { - 1;2} \right]\)và thỏa mãn điều kiện \(f(x) = \sqrt {x + 2} + xf\left( {3 - {x^2}} \right)\). Tính tích phân \(I = \int\limits_{ - 1}^2 {f(x)dx} \).
Ta có
\(\begin{array}{l}f\left( x \right) = \sqrt {x + 2} + xf\left( {3 - {x^2}} \right)\\ \Rightarrow I = \int\limits_{ - 1}^2 {f\left( x \right)dx} = \int\limits_{ - 1}^2 {\sqrt {x + 2} dx} + \int\limits_{ - 1}^2 {xf\left( {3 - {x^2}} \right)dx} \\ \Rightarrow I = {I_1} + {I_2}\end{array}\)
Xét tích phân \({I_1} = \int\limits_{ - 1}^2 {\sqrt {x + 2} dx} \).
Đặt \(t = \sqrt {x + 2} \) \( \Rightarrow {t^2} = x + 2 \Rightarrow 2tdt = dx\).
Đổi cận: \(\left\{ \begin{array}{l}x = - 1 \Rightarrow t = 1\\x = 2 \Rightarrow t = 2\end{array} \right.\).
\( \Rightarrow {I_1} = \int\limits_1^2 {t.2tdt} = 2\int\limits_1^2 {{t^2}dt} = \left. {\dfrac{{2{t^3}}}{3}} \right|_1^2 = \dfrac{{14}}{3}.\)
Xét tích phân \({I_2} = \int\limits_{ - 1}^2 {xf\left( {3 - {x^2}} \right)dx} \).
Đặt \(u = 3 - {x^2} \Rightarrow du = - 2xdx\) \( \Rightarrow xdx = - \dfrac{1}{2}du\).
Đổi cận: \(\left\{ \begin{array}{l}x = 1 \Rightarrow u = 2\\x = 2 \Rightarrow u = - 1\end{array} \right.\).
\( \Rightarrow {I_2} = \int\limits_2^{ - 1} { - \dfrac{1}{2}f\left( u \right)du} = \dfrac{1}{2}\int\limits_{ - 1}^2 {f\left( x \right)dx} = \dfrac{1}{2}I\).
Vậy \(I = \dfrac{{14}}{3} + \dfrac{1}{2}I \Leftrightarrow \dfrac{1}{2}I = \dfrac{{14}}{3} \Leftrightarrow I = \dfrac{{28}}{3}\).
Cho hàm số \(f\left( x \right)\) liên tục trên R thỏa mãn điều kiện \(x.f\left( {{x^3}} \right) + f\left( {{x^2} - 1} \right) = {e^{{x^2}}}\), \(\forall x \in \mathbb{R}\). Khi đó giá trị của \(\int\limits_{ - 1}^0 {f\left( x \right)dx} \) là:
Ta có: \(x.f\left( {{x^3}} \right) + f\left( {{x^2} - 1} \right) = {e^{{x^2}}}\) \( \Leftrightarrow {x^2}.f\left( {{x^3}} \right) + xf\left( {{x^2} - 1} \right) = x{e^{{x^2}}}\).
Lấy tích phân tư -1 đến 0 hai vế phương trình ta có:
\(\int\limits_{ - 1}^0 {{x^2}.f\left( {{x^3}} \right)dx} + \int\limits_{ - 1}^0 {xf\left( {{x^2} - 1} \right)dx} = \int\limits_{ - 1}^0 {x{e^{{x^2}}}dx} \,\,\left( * \right)\).
Xét \({I_1} = \int\limits_{ - 1}^0 {{x^2}.f\left( {{x^3}} \right)dx} \).
Đặt \(t = {x^3} \Rightarrow dt = 3{x^2}dx \Rightarrow {x^2}dx = \dfrac{{dt}}{3}\).
Đổi cận: \(\left\{ \begin{array}{l}x = - 1 \Rightarrow t = - 1\\x = 0 \Rightarrow t = 0\end{array} \right.\), khi đó ta có: \({I_1} = \dfrac{1}{3}\int\limits_{ - 1}^0 {f\left( t \right)dt} = \dfrac{1}{3}\int\limits_{ - 1}^0 {f\left( x \right)dx} \).
Xét \({I_2} = \int\limits_{ - 1}^0 {xf\left( {{x^2} - 1} \right)dx} \).
Đặt \(u = {x^2} - 1 \Rightarrow du = 2xdx \Rightarrow xdx = \dfrac{1}{2}du\).
Đổi cận: \(\left\{ \begin{array}{l}x = - 1 \Rightarrow u = 0\\x = 0 \Rightarrow u = - 1\end{array} \right.\), khi đó ta có \({I_2} = \dfrac{1}{2}\int\limits_0^{ - 1} {f\left( u \right)du} = - \dfrac{1}{2}\int\limits_{ - 1}^0 {f\left( x \right)dx} \).
Xét \({I_3} = \int\limits_{ - 1}^0 {x{e^{{x^2}}}dx} \)
Đặt \(v = {x^2} \Rightarrow dv = 2xdx \Rightarrow xdx = \dfrac{1}{2}dv\).
Đổi cận: \(\left\{ \begin{array}{l}x = - 1 \Rightarrow v = 1\\x = 0 \Rightarrow v = 0\end{array} \right.\), khi đó ta có \({I_3} = \dfrac{1}{2}\int\limits_1^0 {{e^v}dv} = \dfrac{1}{2}\left. {{e^v}} \right|_1^0 = \dfrac{1}{2} - \dfrac{e}{2} = \dfrac{{1 - e}}{2}\).
Thay tất cả vào (*) ta có:
\(\begin{array}{l}\dfrac{1}{3}\int\limits_{ - 1}^0 {f\left( x \right)dx} - \dfrac{1}{2}\int\limits_{ - 1}^0 {f\left( x \right)dx} = \dfrac{{1 - e}}{2}\\ \Leftrightarrow - \dfrac{1}{6}\int\limits_{ - 1}^0 {f\left( x \right)dx} = \dfrac{{1 - e}}{2}\\ \Leftrightarrow \int\limits_{ - 1}^0 {f\left( x \right)dx} = 3\left( {e - 1} \right)\end{array}\)
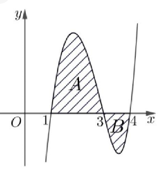
Cho hàm số \(y = f\left( x \right)\) có đồ thị như hình vẽ. Biết các miền \(A\) và \(B\) có diện tích lần lượt là 4 và 1. Tính \(\int\limits_1^2 {4xf\left( {{x^2}} \right)d{\rm{x}}} \)
Đáp án: \(\int\limits_1^2 {4xf\left( {{x^2}} \right)d{\rm{x}}} \)
Đáp án: \(\int\limits_1^2 {4xf\left( {{x^2}} \right)d{\rm{x}}} \)
Bước 1: Đổi biến
Đặt \(t = {x^2} \Rightarrow dt = 2xdx\).
Đổi cận: \(\left\{ \begin{array}{l}x = 1 \Rightarrow t = 1\\x = 2 \Rightarrow t = 4\end{array} \right.\).
Bước 2:
Khi đó ta có \(I = \int\limits_1^2 {4xf\left( {{x^2}} \right)dx} = \int\limits_1^4 {2f\left( t \right)dt} \)\( = 2\int\limits_1^4 {f\left( x \right)dx} \)\( = 2\left[ {\int\limits_1^3 {f\left( x \right)dx}+\int\limits_3^4 {f\left( x \right)dx}} \right] \)\( = 2\left( {4 - 1} \right) = 6\).
Cho hàm số \(f\left( x \right)\) liên tục trên đoạn \(\left[ {0;1} \right]\) và \(\int\limits_0^{\frac{\pi }{2}} {f\left( {\sin x} \right)} dx = 5\). Tính \(I = \int\limits_0^\pi {xf\left( {\sin x} \right)} dx\).
Ta có: \(I = \int\limits_0^\pi {xf\left( {\sin x} \right)dx} = \int\limits_0^{\frac{\pi }{2}} {xf\left( {\sin x} \right)dx} + \int\limits_{\frac{\pi }{2}}^\pi {xf\left( {\sin x} \right)dx} \)
Xét \({I_1} = \int\limits_{\frac{\pi }{2}}^\pi {xf\left( {\sin x} \right)dx} \), đặt \(t = \pi - x \Rightarrow dt = - dx\).
Đổi cận: \(\left\{ \begin{array}{l}x = \dfrac{\pi }{2} \Rightarrow t = \dfrac{\pi }{2}\\x = \pi \Rightarrow t = 0\end{array} \right.\).
Khi đó ta có:
\(\begin{array}{l}{I_1} = - \int\limits_{\frac{\pi }{2}}^0 {\left( {\pi - t} \right)f\left( {\sin \left( {\pi - t} \right)} \right)\,} dt\\\,\,\,\,\,\, = \int\limits_0^{\frac{\pi }{2}} {\left( {\pi - t} \right)f\left( {\sin t} \right)\,} dt\\\,\,\,\,\,\, = \int\limits_0^{\frac{\pi }{2}} {\left( {\pi - x} \right)f\left( {\sin x} \right)\,} dx\\\,\,\,\,\,\, = \pi \int\limits_0^{\frac{\pi }{2}} {f\left( {\sin x} \right)\,} dx - \int\limits_0^{\frac{\pi }{2}} {xf\left( {\sin x} \right)\,} dx\end{array}\)
\(\begin{array}{l} \Rightarrow I = \int\limits_0^{\frac{\pi }{2}} {xf\left( {\sin x} \right)dx} + \pi \int\limits_0^{\frac{\pi }{2}} {f\left( {\sin x} \right)\,} dx - \int\limits_0^{\frac{\pi }{2}} {xf\left( {\sin x} \right)\,} dx\\ \Rightarrow I = \pi \int\limits_0^{\frac{\pi }{2}} {f\left( {\sin x} \right)\,} dx = 5\pi .\end{array}\).
Biết \(\int\limits_{0}^{1}{\frac{\pi {{x}^{3}}+{{2}^{x}}+\text{e}{{x}^{3}}{{.2}^{x}}}{\pi +\text{e}{{.2}^{x}}}\text{d}x}=\frac{1}{m}+\frac{1}{\text{e}\ln n}\ln \left( p+\frac{\text{e}}{\text{e}+\pi } \right)\) với \(m\), \(n\), \(p\) là các số nguyên dương. Tính tổng \(S=m+n+p\).
Ta có \(\int\limits_{0}^{1}{\frac{\pi {{x}^{3}}+{{2}^{x}}+\text{e}{{x}^{3}}{{.2}^{x}}}{\pi +\text{e}{{.2}^{x}}}\text{d}x}=\int\limits_{0}^{1}{\left( {{x}^{3}}+\frac{{{2}^{x}}}{\pi +\text{e}{{.2}^{x}}} \right)\text{d}x}\) \(=\left. \frac{{{x}^{4}}}{4} \right|_{0}^{1}+\int\limits_{0}^{1}{\frac{{{2}^{x}}}{\pi +\text{e}{{.2}^{x}}}\text{d}x}=\frac{1}{4}+\int\limits_{0}^{1}{\frac{{{2}^{x}}}{\pi +\text{e}{{.2}^{x}}}\text{d}x}=\frac{1}{4}+J.\)
Tính \(J=\int\limits_{0}^{1}{\frac{{{2}^{x}}}{\pi +\text{e}{{.2}^{x}}}\text{d}x}\).
Đặt \(\pi +\text{e}{{.2}^{x}}=t\Rightarrow \text{e}{{.2}^{x}}\ln 2\text{d}x=\text{d}t\Leftrightarrow {{2}^{x}}\text{d}x=\frac{1}{\text{e}.\ln 2}\text{d}t\).
Đổi cận: Khi \(x=0\) thì \(t=\pi +\text{e}\); khi \(x=1\) thì \(t=\pi +2\text{e}\).
Khi đó \(J=\int\limits_{0}^{1}{\frac{{{2}^{x}}}{\pi +\text{e}{{.2}^{x}}}\text{d}x}=\frac{1}{\text{e}\ln 2}\int\limits_{\pi +\text{e}}^{\pi +2\text{e}}{\frac{1}{t}\text{d}t}=\frac{1}{\text{e}\ln 2}\left. \ln \left| t \right| \right|_{\pi +\text{e}}^{\pi +2\text{e}}=\frac{1}{\text{e}\ln 2}\ln \left( 1+\frac{\text{e}}{\text{e}+\pi } \right)\).
Suy ra \(\int\limits_{0}^{1}{\frac{\pi {{x}^{3}}+{{2}^{x}}+\text{e}{{x}^{3}}{{.2}^{x}}}{\pi +\text{e}{{.2}^{x}}}\text{d}x}=\frac{1}{4}+\frac{1}{\text{e}\ln 2}\ln \left( 1+\frac{\text{e}}{\text{e}+\pi } \right)\)\(\Rightarrow m=4\), \(n=2\), \(p=1\).
Vậy \(S=7\).
Cho tích phân \(I = \int\limits_1^{\sqrt 3 } {\dfrac{{\sqrt {1 + {x^2}} }}{{{x^2}}}dx} \). Nếu đổi biến số \(t = \dfrac{{\sqrt {{x^2} + 1} }}{x}\) thì:
Đặt
\(\begin{array}{l}t = \dfrac{{\sqrt {{x^2} + 1} }}{x} \Leftrightarrow {t^2} = \dfrac{{{x^2} + 1}}{{{x^2}}} = 1 + \dfrac{1}{{{x^2}}}\\ \Rightarrow 2tdt = - \dfrac{2}{{{x^3}}}dx \Rightarrow tdt = - \dfrac{{dx}}{{{x^3}}}\end{array}\)
Và \({t^2}{x^2} = {x^2} + 1 \Rightarrow {x^2}\left( {{t^2} - 1} \right) = 1 \Leftrightarrow {x^2} = \dfrac{1}{{{t^2} - 1}} \Rightarrow \dfrac{{dx}}{x} = - \dfrac{t}{{{t^2} - 1}}dt\)
Đổi cận: \(\left\{ \begin{array}{l}x = 1 \Rightarrow t = \sqrt 2 \\x = \sqrt 3 \Rightarrow t = \dfrac{2}{{\sqrt 3 }}\end{array} \right.\)
Khi đó ta có: \(I = - \int\limits_{\sqrt 2 }^{\dfrac{2}{{\sqrt 3 }}} {\dfrac{{{t^2}}}{{{t^2} - 1}}dt} \)
Với mỗi số \(k\), đặt \({I_k} = \int\limits_{ - \sqrt k }^{\sqrt k } {\sqrt {k - {x^2}} dx} \). Khi đó \({I_1} + {I_2} + {I_3} + ... + {I_{12}}\) bằng:
Đặt \(x = \sqrt k \sin t\) \( \Rightarrow dx = \sqrt k \cos tdt\).
Đổi cận: \(\left\{ \begin{array}{l}x = - \sqrt k \Leftrightarrow \sin t = - 1 \Leftrightarrow t = - \dfrac{\pi }{2}\\x = \sqrt k \Leftrightarrow \sin t = 1 \Leftrightarrow t = \dfrac{\pi }{2}\end{array} \right.\).
Khi đó ta có
\(\begin{array}{l}{I_k} = \int\limits_{ - \dfrac{\pi }{2}}^{\dfrac{\pi }{2}} {\sqrt {k - k{{\sin }^2}t} .\sqrt k \cos tdt} \\{I_k} = \int\limits_{ - \dfrac{\pi }{2}}^{\dfrac{\pi }{2}} {k{{\cos }^2}tdt} \\{I_k} = k\int\limits_{ - \dfrac{\pi }{2}}^{\dfrac{\pi }{2}} {\dfrac{{1 + \cos 2t}}{2}dt} \\{I_k} = \dfrac{k}{2}\left. {\left( {t + \dfrac{1}{2}\sin 2t} \right)} \right|_{ - \dfrac{\pi }{2}}^{\dfrac{\pi }{2}}\\{I_k} = \dfrac{k}{2}\left( {\dfrac{\pi }{2} + \dfrac{1}{2}\sin \pi + \dfrac{\pi }{2} - \dfrac{1}{2}\sin \left( { - \pi } \right)} \right)\\{I_k} = \dfrac{k}{2}.\pi = \dfrac{{k\pi }}{2}\end{array}\)
\(\begin{array}{l} \Rightarrow {I_1} + {I_2} + {I_3} + ... + {I_{12}}\\ = \dfrac{\pi }{2}\left( {1 + 2 + 3 + ... + 12} \right)\\ = \dfrac{\pi }{2}.\dfrac{{12.13}}{2} = 39\pi \end{array}\)
Cho \(\int_0^{\frac{\pi }{{18}}} f (\sin (3x))\cos (3x)dx = 3\) và \(\int_{\frac{1}{2}}^2 f (1 - x)dx = 4\). Tính \(I = \int_{ - 1}^0 f (x)d\)
$I=$
$I=$
Bước 1: Tính \(\int_0^{\frac{\pi }{{18}}} f (\sin (3x))d(\sin 3x) = 9\), \(\int_0^{\frac{1}{2}} f (x)dx\)
Ta có: \(\int_0^{\frac{\pi }{{18}}} f (\sin (3x))\cos (3x)dx\)\( = \frac{1}{3}\int_0^{\frac{\pi }{{18}}} f (\sin (3x))d(\sin 3x) = 3\)
\( \Rightarrow \int_0^{\frac{\pi }{{18}}} f (\sin (3x))d(\sin 3x) = 9\)
\( \Rightarrow \int_0^{\frac{\pi }{{18}}} f (\sin (3x))d(\sin 3x)\)\( = \int_0^{\frac{1}{2}} f (x)dx = 9\)
Bước 2: Tính \(\int_{ - 1}^{\frac{1}{2}} f (x) \cdot dx\) và \(I = \int_{ - 1}^0 f (x)d\)
Lại có \(\int_{\frac{1}{2}}^2 f (1 - x)dx = 4\). Đặt \(u = 1 - x \Rightarrow du = - dx\).
Đổi cận: \(x = \dfrac{1}{2} \Rightarrow t = \dfrac{1}{2};x = 2 \Rightarrow t = - 1\).
\( \Rightarrow \int_{\frac{1}{2}}^2 f (1 - x)dx\)\( = \int_{\frac{1}{2}}^{ - 1} f (u) \cdot ( - du)\)\( = \int_{ - 1}^{\frac{1}{2}} f (u) \cdot du = \int_{ - 1}^{\frac{1}{2}} f (x) \cdot dx = 4\)
Khi đó, \(I = \int_{ - 1}^0 f (x)dx\)\( = \int_{ - 1}^{\frac{1}{2}} f (x)dx - \int_0^{\frac{1}{2}} f (x)dx\)\( = 4 - 9 = - 5\).

