Trong không gian với hệ tọa độ \(Oxyz\), cho đường thẳng \(\Delta :\left\{ \begin{array}{l}x = 2 + \left( {{m^2} - 2m} \right)t\\y = 5 - \left( {m - 4} \right)t\\z = 7 - 2\sqrt 2 \end{array} \right.\) và điểm \(A\left( {1;2;3} \right)\). Gọi \(S\) là tập các giá trị thực của tham số \(m\) để khoảng cách từ \(A\) đến đường thẳng \(\Delta \) có giá trị nhỏ nhất. Tổng các phần tử của \(S\) là
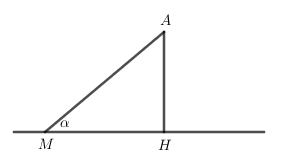
Đường thẳng \(\Delta \) đi qua điểm \(M\left( {2;5;7 - 2\sqrt 2 } \right)\) và nhận \(\overrightarrow u = \left( {{m^2} - 2m;4 - m;0} \right)\) làm VTCP.
Có \(\overrightarrow {AM} = \left( {1;3;4 - 2\sqrt 2 } \right) \Rightarrow AM= \sqrt{34 - 16\sqrt 2} \).
Để \(d\left( {A,\Delta } \right) = A{H_{\min }}\) thì \(\sin \alpha = \dfrac{{AH}}{{AM}}\) đạt GTNN hay \(\cos \alpha \) đạt GTLN.
Mà \(\cos \alpha = \cos \left( {AM,\Delta } \right) = \dfrac{{\left| {\overrightarrow {AM} .\overrightarrow u } \right|}}{{\left| {\overrightarrow {AM} } \right|.\left| {\overrightarrow u } \right|}} = \dfrac{{\left| {\left( {{m^2} - 2m} \right) + 3\left( {4 - m} \right)} \right|}}{{ {\sqrt{34 - 16\sqrt 2} }.\sqrt {{{\left( {{m^2} - 2m} \right)}^2} + {{\left( {4 - m} \right)}^2}} }}\)
Mà \(\left| {\left( {{m^2} - 2m} \right) + 3\left( {4 - m} \right)} \right| \le \sqrt {{1^2} + {3^2}} .\sqrt {{{\left( {{m^2} - 2m} \right)}^2} + {{\left( {4 - m} \right)}^2}} \)
\( \Rightarrow \dfrac{{\left| {\left( {{m^2} - 2m} \right) + 3\left( {4 - m} \right)} \right|}}{{ {\sqrt{34 - 16\sqrt 2} }.\sqrt {{{\left( {{m^2} - 2m} \right)}^2} + {{\left( {4 - m} \right)}^2}} }} \le \dfrac{{\sqrt {10} }}{{\sqrt{34 - 16\sqrt 2} }}\)
\( \Rightarrow \cos \alpha \) đạt GTLN nếu \(\dfrac{{{m^2} - 2m}}{1} = \dfrac{{4 - m}}{3} \Leftrightarrow 3{m^2} - 6m = 4 - m \Leftrightarrow 3{m^2} - 5m - 4 = 0\)
Phương trình này có hai nghiệm phân biệt do \(ac < 0\) nên tổng các giá trị của \(m\) là \(\dfrac{5}{3}\) .
Trong không gian \(Oxyz\), cho đường thẳng \(d:\,\,\dfrac{{x - 3}}{1} = \dfrac{{y - 4}}{1} = \dfrac{{z - 5}}{{ - 2}}\) và các điểm \(A\left( {3 + m;\,\,4 + m;\,\,5 - 2m} \right)\), \(B\left( {4 - n;\,\,5 - n;\,\,3 + 2n} \right)\) với \(m,\,\,n\) là các số thực. Khẳng định nào sau đây đúng?
- Thay tọa độ điểm \(A\left( {3 + m;\,\,4 + m;\,\,5 - 2m} \right)\) vào phương trình đường thẳng \(d\) ta có:
\(\dfrac{{3 + m - 3}}{1} = \dfrac{{4 + m - 4}}{1} = \dfrac{{5 - 2m - 5}}{{ - 2}} \Leftrightarrow m = m = m\) (luôn đúng) \( \Rightarrow A \in d\).
- Thay tọa độ điểm \(B\left( {4 - n;\,\,5 - n;\,\,3 + 2n} \right)\) vào phương trình đường thẳng \(d\) ta có:
\(\dfrac{{4 - n - 3}}{1} = \dfrac{{5 - n - 4}}{1} = \dfrac{{3 + 2n - 5}}{{ - 2}} \Leftrightarrow 1 - n = 1 - n = 1 - n\) (luôn đúng) \( \Rightarrow B \in d\).
Vậy \(A \in d,\,\,B \in d\).

