Cho \(x;y\) là hai số thực dương thỏa mãn \(x \ne y\) và \({\left( {{2^x} + \dfrac{1}{{{2^x}}}} \right)^y} < {\left( {{2^y} + \dfrac{1}{{{2^y}}}} \right)^x}.\) Tìm giá trị nhỏ nhất của biểu thức \(P = \dfrac{{{x^2} + 3{y^2}}}{{xy - {y^2}}}\).
Ta có
\(\begin{array}{l}P = \dfrac{{{x^2} + 3{y^2}}}{{xy - {y^2}}}\\ \Leftrightarrow Pxy - P{y^2} = {x^2} + 3{y^2}\\ \Leftrightarrow \left( {P + 3} \right){y^2} - Pxy + {x^2} = 0\end{array}\)
Phương trình trên có nghiệm khi
\(\begin{array}{l}\Delta = {P^2}{x^2} - 4\left( {P + 3} \right){x^2} \ge 0\\ \Leftrightarrow {P^2} - 4P - 12 \ge 0\\ \Rightarrow \left[ \begin{array}{l}P \ge 6\\P \le - 2\end{array} \right. \Rightarrow MinP = 6\end{array}\)
Dấu bằng xáy ra khi \(\left\{ \begin{array}{l}y = \dfrac{{Px}}{{2\left( {P + 3} \right)}} = \dfrac{x}{3}\\\dfrac{{{x^2} + 3{y^2}}}{{xy - {y^2}}} = 6\end{array} \right. \Rightarrow x = 3y\)
Dễ thấy \(x=3y\) thỏa mãn điều kiện bài cho vì:
$\begin{array}{l}
{\left( {{2^{3y}} + \frac{1}{{{2^{3y}}}}} \right)^y} < {\left( {{2^y} + \frac{1}{{{2^y}}}} \right)^{3y}}\\
\Leftrightarrow {2^{3y}} + \frac{1}{{{2^{3y}}}} < {\left( {{2^y} + \frac{1}{{{2^y}}}} \right)^3}\\
\Leftrightarrow {2^{3y}} + \frac{1}{{{2^{3y}}}} < {2^{3y}} + \frac{1}{{{2^{3y}}}} + {3.2^y}.\frac{1}{{{2^y}}}.\left( {{2^y} + \frac{1}{{{2^y}}}} \right)\\
\Leftrightarrow 0 < 3\left( {{2^y} + \frac{1}{{{2^y}}}} \right)
\end{array}$
Bđt trên luôn đúng với mọi \(y>0\).
Cho hàm số \(y = f\left( x \right)\). Hàm số \(y = f'\left( x \right)\) có bảng biến thiên như sau:
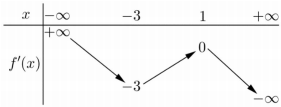
Bất phương trình \(f\left( x \right) < {e^x} + m\) đúng với mọi \(x \in \left( { - 1;1} \right)\) khi và chỉ khi:
Theo đề bài ta có : \(f\left( x \right) < {e^x} + m \Leftrightarrow f\left( x \right) - {e^x} < m\)
Đặt \(g\left( x \right) = f\left( x \right) - {e^x}.\) Khi đó :
\(\begin{array}{l}f\left( x \right) < {e^x} + m\,\,\forall x \in \left( { - 1;1} \right)\\ \Rightarrow g\left( x \right) = f\left( x \right) - {e^x} < m\,\,\forall x \in \left( { - 1;1} \right)\\ \Leftrightarrow m \ge \mathop {\max }\limits_{\left[ { - 1;1} \right]} g\left( x \right)\\g'\left( x \right) = f'\left( x \right) - {e^x}\end{array}\)
Trên \(\left( { - 1;1} \right)\) ta có \(f'\left( x \right) < 0;\,\,{e^x} > 0\,\,\forall x \in R \Rightarrow g'\left( x \right) < 0\,\,\forall x \in \left( { - 1;1} \right)\)
\( \Rightarrow g\left( x \right)\) nghịch biến trên \(\left( { - 1;\;1} \right).\)
\(\begin{array}{l} \Rightarrow \mathop {\max }\limits_{\left[ { - 1;1} \right]} g\left( x \right) = g\left( { - 1} \right) = f\left( { - 1} \right) - {e^{ - 1}} = f\left( { - 1} \right) - \dfrac{1}{e}\\ \Rightarrow m \ge f\left( { - 1} \right) - \dfrac{1}{e}.\end{array}\)

