Bài toán cực trị có tham số đối với một số hàm số cơ bản

ĐKXĐ: \(D = \mathbb{R}\backslash \left\{ { - 1} \right\}\).

Ta có: \(y = \dfrac{{{x^2} + mx + 2m}}{{x + 1}} = x + m - 1 + \dfrac{{m + 1}}{{x + 1}}\).

\( \Rightarrow y' = 1 - \dfrac{{m + 1}}{{{{\left( {x + 1} \right)}^2}}} = \dfrac{{{x^2} + 2x - m}}{{{{\left( {x + 1} \right)}^2}}}\)

Để hàm số đã cho có 2 cực trị thì phương trình \(y' = 0\) phải có 2 nghiệm phân biệt khác \( - 1\).

\( \Leftrightarrow \left\{ \begin{array}{l}\Delta ' = 1 + m > 0\\1 - 2 - m \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}m >  - 1\\m \ne  - 1\end{array} \right. \Leftrightarrow m >  - 1.\)

Khi đó, giả sử \({x_1},\,\,{x_2}\) là nghiệm phân biệt của phương trình \(y' = 0\), áp dụng định lí Vi-ét ta có \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - 2\\{x_1}.{x_2} =  - m\end{array} \right..\)

Đặt \(A\left( {{x_1};{x_1} + m - 1 + \dfrac{{m + 1}}{{{x_1} + 1}}} \right),\,\,B\left( {{x_2};{x_2} + m - 1 + \dfrac{{m + 1}}{{{x_2} + 1}}} \right)\) là hai điểm cực trị của hàm số.

Để tam giác \(OAB\) vuông tại \(O\) thì  \(\overrightarrow {OA} .\overrightarrow {OB}  = 0\).

\(\begin{array}{l} \Leftrightarrow {x_1}.{x_2} + \left( {{x_1} + m - 1 + \dfrac{{m + 1}}{{{x_1} + 1}}} \right)\left( {{x_2} + m - 1 + \dfrac{{m + 1}}{{{x_2} + 1}}} \right) = 0\\ \Leftrightarrow 2{x_1}{x_2} + \left( {m - 1} \right)\left( {{x_1} + {x_2}} \right) + \left( {m + 1} \right)\left( {\dfrac{{{x_1}}}{{{x_2} + 1}} + \dfrac{{{x_2}}}{{{x_1} + 1}}} \right)\\\,\,\,\,\,\,\,\,\, + {\left( {m - 1} \right)^2} + \left( {{m^2} - 1} \right)\left( {\dfrac{1}{{{x_1} + 1}} + \dfrac{1}{{{x_2} + 1}}} \right) + \dfrac{{{{\left( {m + 1} \right)}^2}}}{{\left( {{x_1} + 1} \right)\left( {{x_2} + 1} \right)}} = 0\\ \Leftrightarrow 2{x_1}{x_2} + \left( {m - 1} \right)\left( {{x_1} + {x_2}} \right) + \left( {m + 1} \right)\dfrac{{x_1^2 + x_2^2 + {x_1} + {x_2}}}{{{x_1}{x_2} + {x_1} + {x_2} + 1}}\\\,\,\,\,\,\,\,\,\, + {\left( {m - 1} \right)^2} + \left( {{m^2} - 1} \right)\dfrac{{{x_1} + {x_2} + 2}}{{{x_1}{x_2} + {x_1} + {x_2} + 1}} + \dfrac{{{{\left( {m + 1} \right)}^2}}}{{{x_1}{x_2} + {x_1} + {x_2} + 1}} = 0\\ \Leftrightarrow 2{x_1}{x_2} + \left( {m - 1} \right)\left( {{x_1} + {x_2}} \right) + \left( {m + 1} \right)\dfrac{{{{\left( {{x_1} + {x_2}} \right)}^2} - 2{x_1}{x_2} + {x_1} + {x_2}}}{{{x_1}{x_2} + {x_1} + {x_2} + 1}}\\\,\,\,\,\,\,\,\,\, + {\left( {m - 1} \right)^2} + \left( {{m^2} - 1} \right)\dfrac{{{x_1} + {x_2} + 2}}{{{x_1}{x_2} + {x_1} + {x_2} + 1}} + \dfrac{{{{\left( {m + 1} \right)}^2}}}{{{x_1}{x_2} + {x_1} + {x_2} + 1}} = 0\\ \Leftrightarrow  - 2m - 2\left( {m - 1} \right) + \left( {m + 1} \right).\dfrac{{2 + 2m}}{{ - m - 1}} + {\left( {m - 1} \right)^2} + \dfrac{{{{\left( {m + 1} \right)}^2}}}{{ - m - 1}} = 0\\ \Leftrightarrow  - 2m - 2m + 2 - 2 - 2m + {m^2} - 2m + 1 - m - 1 = 0\\ \Leftrightarrow {m^2} - 9m = 0 \Leftrightarrow \left[ \begin{array}{l}m = 0\\m = 9\end{array} \right.\,\,\left( {tm} \right)\end{array}\)

\( \Rightarrow S = \left\{ {0;9} \right\}\).

Vậy tổng tất cả các phần tử của S là \(9\).

Để đồ thị hàm số \(y = m{x^3} - \left( {2m - 1} \right){x^2} + 2mx - m - 1\) có hai điểm cực trị nằm về hai phía của trục hoành thì phương trình \(m{x^3} - \left( {2m - 1} \right){x^2} + 2mx - m - 1 = 0\,\,\left( * \right)\) phải có 3 nghiệm phân biệt.

Ta có:

\(\begin{array}{l}\,\,\,\,\,m{x^3} - \left( {2m - 1} \right){x^2} + 2mx - m - 1 = 0\\ \Leftrightarrow \left( {x - 1} \right)\left[ {m{x^2} - \left( {m - 1} \right)x + m + 1} \right] = 0\\ \Leftrightarrow \left[ \begin{array}{l}x = 1\\m{x^2} - \left( {m - 1} \right)x + m + 1 = 0\,\,\,\left( {**} \right)\end{array} \right.\end{array}\)

Để (*) có ba nghiệm phân biệt thì (**) phải có 2 nghiệm phân biệt khác 1.

\(\begin{array}{l} \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m.1 - \left( {m - 1} \right).1 + m + 1 \ne 0\\\Delta  = {\left( {m - 1} \right)^2} - 4m\left( {m + 1} \right) > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m - m + 1 + m + 1 \ne 0\\{m^2} - 2m + 1 - 4{m^2} - 4m > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne  - 2\\ - 3{m^2} - 6m + 1 > 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}m \ne 0\\m \ne  - 2\\\dfrac{{ - 3 - 2\sqrt 3 }}{3} < m < \dfrac{{ - 3 + 2\sqrt 3 }}{3}\end{array} \right.\end{array}\)

Mà \(m \in \mathbb{Z}\) \( \Rightarrow m =  - 1\).

Vậy có 1 giá trị của \(m\) thỏa mãn yêu cầu bài toán.

Xét hàm số \(f\left( x \right) = 3{x^4} - 4{x^3} - 12{x^2}\) ta có

\(\begin{array}{l}f'\left( x \right) = 12{x^3} - 12{x^2} - 24x\\f'\left( x \right) = 0 \Leftrightarrow 12{x^3} - 12{x^2} - 24x = 0 \Leftrightarrow \left[ \begin{array}{l}x = 0\\x =  - 1\\x = 2\end{array} \right.\end{array}\)

BBT:

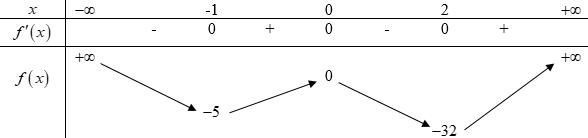
Ta có đồ thị \(y = f\left( x \right)\,\,\left( C \right)\) như sau:

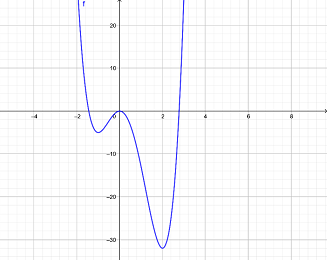
Để \(y = \left| {3{x^4} - 4{x^3} - 12{x^2} + m} \right|\) có 5 điểm cực trị thì:

TH1: \(\left( C \right)\) cắt đường thẳng \(y =  - m\) tại 2 điểm phân biệt khác cực trị

\( \Leftrightarrow \left[ \begin{array}{l} - m > 0\\ - 32 <  - m <  - 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m < 0\\5 < m < 32\end{array} \right.\)

Mà \(m \in {\mathbb{Z}^ + }\, \Rightarrow m \in \left\{ {6;7;...;31} \right\}\) : 26 giá trị.

TH2: \(\left( C \right)\) cắt đường thẳng \(y =  - m\) tại 3 điểm phân biệt, trong đó có 1 cực trị

\( \Leftrightarrow \left[ \begin{array}{l} - m = 0\\ - m =  - 5\end{array} \right. \Leftrightarrow \left[ \begin{array}{l}m = 0\,(L)\\m = 5\,(TM)\end{array} \right.\)

Vậy, có tất cả 27 giá trị của m thỏa mãn.

Bước 1:

Số điểm cực trị của hàm số \(y = f\left( {\left| x \right|} \right)\) là \(2m + 1\) trong đó \(m\) là số điềm cực trị dương của hàm số \(y = f\left( x \right)\).

Do đó để hàm số \(y = f\left( {\left| x \right|} \right)\) có đúng 3 điểm cực trị thì \(m = 1 \Rightarrow \) hàm số \(y = f\left( x \right)\) phải có 1 điểm cực trị dương (*).

Bước 2:

Ta có: \(f'\left( x \right) = {x^2} + 2mx + {m^2} - 4\).

Xét \(f'\left( x \right) = 0\) có \(\Delta ' = {m^2} - {m^2} + 4 > 0\,\,\forall m\) nên \(f'\left( x \right) = 0\) có 2 nghiệm phân biệt \(\left[ \begin{array}{l}{x_1} =  - m + 2\\{x_2} =  - m - 2\end{array} \right.\).

Bước 3:

\(\left( * \right) \Rightarrow  - m - 2 \le 0 <  - m + 2 \Leftrightarrow  - 2 \le m < 2\).

Mà \(m \in \mathbb{Z}\) \( \Rightarrow m \in \left\{ { - 2; - 1;0;1} \right\}\).

Vậy có 4 giá trị của \(m\) thỏa mãn yêu cầu bài toán.

Ta có: \(y' = {x^2} - 2x + {m^2} - 8m + 16\).

Để hàm số đã cho có cực trị thì phương trình \(y' = 0\) phải có 2 nghiệm phân biệt.

\(\begin{array}{l} \Rightarrow \Delta ' = 1 - {m^2} + 8m - 16 > 0\\ \Leftrightarrow  - {m^2} + 8m - 15 > 0\\ \Leftrightarrow 3 < m < 5\end{array}\)

Mà \(m \in \mathbb{Z} \Rightarrow m = 4\).

Vậy có 1 giá trị của \(m\) thỏa mãn yêu cầu bài toán.

$=>k=1$

Để hàm số \(y =  - {x^3} - 3{x^2} + mx + 2\) có cực đại và cực tiểu thì phương trình \(y' =  - 3{x^2} - 6x + m = 0\) phải có 2 nghiệm phân biệt \( \Rightarrow \Delta ' = 9 + 3m > 0 \Leftrightarrow m >  - 3\).