Có một lượng kim loại xác định dùng làm dây dẫn. Nếu làm dây với đường kính \(1mm\) thì điện trở của dây là \(16\Omega \). Nếu làm dây bằng dây dẫn có đường kính \(2mm\) thì điện trở của dây thu được là bao nhiêu? Biết chiều dài của dây trong hai trường hợp không thay đổi.
+ Khi dây có đường kính \({d_1} = 1mm\), ta có: \(\left\{ \begin{array}{l}{S_1} = \dfrac{{\pi d_1^2}}{4}\\{R_1} = \rho \dfrac{l}{{{S_1}}}\end{array} \right.\)
+ Khi dây có đường kính \({d_2} = 2mm\) , ta có: \(\left\{ \begin{array}{l}{S_2} = \dfrac{{\pi d_2^2}}{4}\\{R_2} = \rho \dfrac{l}{{{S_2}}}\end{array} \right.\)
Ta suy ra: \(\dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{{S_2}}}{{{S_1}}} = \dfrac{{d_2^2}}{{d_1^2}} = \dfrac{{{2^2}}}{{{1^2}}} = 4\)
\( \Rightarrow {R_2} = \dfrac{{{R_1}}}{4} = \dfrac{{16}}{4} = 4\Omega \)
Người ta cần một điện trở \(100\Omega \) bằng một dây nicrom có đường kính \(0,4mm\). Điện trở suất nicrom \(\rho = {110.10^{ - 8}}\Omega .m\). Đoạn dây phải dùng có chiều dài bằng:
Ta có, điện trở của dây dẫn \(R = \rho \dfrac{l}{S}\) (1)
Theo đề bài, ta có: \(\left\{ \begin{array}{l}R = 100\Omega \\d = 0,4mm\\\rho = {110.10^{ - 8}}\Omega .m\end{array} \right.\) (2)
Tiết diện dây: \(S = \pi {r^2} = \pi \dfrac{{{d^2}}}{4} = \pi .\dfrac{{{{\left( {0,{{4.10}^{ - 3}}} \right)}^2}}}{4} = 1,{26.10^{ - 7}}{m^2}\) (3)
Từ (1), (2) và (3) ta suy ra: \(l = \dfrac{{RS}}{\rho } = \dfrac{{100.1,{{27.10}^{ - 7}}}}{{{{110.10}^{ - 8}}}} = 11,4m\)
Có một lượng kim loại xác định dùng làm dây dẫn. Nếu làm dây với đường kính \(1mm\) thì điện trở của dây là \(16\Omega \). Nếu làm dây bằng dây dẫn có đường kính \(2mm\) thì điện trở của dây thu được là bao nhiêu? Biết chiều dài của dây trong hai trường hợp không thay đổi.
+ Khi dây có đường kính \({d_1} = 1mm\), ta có: \(\left\{ \begin{array}{l}{S_1} = \dfrac{{\pi d_1^2}}{4}\\{R_1} = \rho \dfrac{l}{{{S_1}}}\end{array} \right.\)
+ Khi dây có đường kính \({d_2} = 2mm\) , ta có: \(\left\{ \begin{array}{l}{S_2} = \dfrac{{\pi d_2^2}}{4}\\{R_2} = \rho \dfrac{l}{{{S_2}}}\end{array} \right.\)
Ta suy ra: \(\dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{{S_2}}}{{{S_1}}} = \dfrac{{d_2^2}}{{d_1^2}} = \dfrac{{{2^2}}}{{{1^2}}} = 4\)
\( \Rightarrow {R_2} = \dfrac{{{R_1}}}{4} = \dfrac{{16}}{4} = 4\Omega \)
Người ta cần một điện trở \(100\Omega \) bằng một dây nicrom có đường kính \(0,4mm\). Điện trở suất nicrom \(\rho = {110.10^{ - 8}}\Omega .m\). Đoạn dây phải dùng có chiều dài bằng:
Ta có, điện trở của dây dẫn \(R = \rho \dfrac{l}{S}\) (1)
Theo đề bài, ta có: \(\left\{ \begin{array}{l}R = 100\Omega \\d = 0,4mm\\\rho = {110.10^{ - 8}}\Omega .m\end{array} \right.\) (2)
Tiết diện dây: \(S = \pi {r^2} = \pi \dfrac{{{d^2}}}{4} = \pi .\dfrac{{{{\left( {{{0,4.10}^{ - 3}}} \right)}^2}}}{4} = {1,26.10^{ - 7}}{m^2}\) (3)
Từ (1), (2) và (3) ta suy ra: \(l = \dfrac{{RS}}{\rho } = \dfrac{{{{100.1,27.10}^{ - 7}}}}{{{{110.10}^{ - 8}}}} = 11,4m\)
Cho mạch điện như hình vẽ:
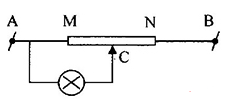
Biết trở có điện trở toàn phần \({R_0} = 12\Omega \), đèn Đ có ghi \(6V - 3W\), \({U_{AB}} = 15V\). Điện trở \({R_{CM}} = ?\) để đèn sáng bình thường.
+ Mạch điện được vẽ lại như hình:
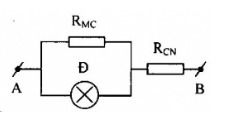
+ Ta đặt, \({R_{MC}} = x\left( \Omega \right)\) với điều kiện \(0 < x < 12\)
\( \Rightarrow {R_{CN}} = 12 - x\left( \Omega \right)\)
+ Khi đèn sáng bình thường, cường độ dòng điện qua đèn \({I_D} = \dfrac{{{P_D}}}{{{U_D}}} = \dfrac{3}{6} = 0,5W\)
+ Ta có \(\left[ {D//{R_{CM}}} \right]nt{R_{CN}}\) nên:
\({U_{CM}} = {U_D} = 6V\)
\({U_{CN}} = {U_{AB}} - {U_D} = 15 - 6 = 9V\)
+ Mặt khác, ta có: \({I_{CN}} = {I_{CM}} + {I_D}\) (1)
Trong đó: \(\left\{ \begin{array}{l}{I_D} = 0,5\\{I_{CM}} = \dfrac{{{U_{CM}}}}{{{R_{CM}}}} = \dfrac{6}{x}\\{I_{CN}} = \dfrac{{{U_{CN}}}}{{{R_{CN}}}} = \dfrac{9}{{12 - x}}\end{array} \right.\)
Ta suy ra: \(\left( 1 \right) \Leftrightarrow \dfrac{9}{{12 - x}} = \dfrac{6}{x} + 0,5\)
\(\begin{array}{l} \Leftrightarrow 0,5{x^2} + 9x - 72 = 0\\ \Rightarrow \left[ \begin{array}{l}x = 6\Omega \\x = - 24\Omega \left( {loai} \right)\end{array} \right.\end{array}\)
Vậy với \({R_{CM}} = 6\Omega \) thì khi đó đèn sáng bình thường.
Cho mạch điện như hình vẽ:

Khi dịch chuyển con chạy về phía A, độ sáng của đèn thay đổi như thế nào?
+ Mạch điện được vẽ lại như hình:

+ Khi dịch chuyển con chạy C về phía A
\( \Rightarrow {R_{CM}}\) giảm dần, nhưng ta chưa thể kết luận về độ sáng của đèn thay đổi như thế nào được, mà cần phải tìm cường độ dòng điện qua đèn thay đổi như thế nào khi con chạy C dịch chuyển về phía A.
Ta có:
+ Điện trở của bóng đèn: \({R_D} = \dfrac{{U_D^2}}{{{P_D}}} = \dfrac{{{6^2}}}{3} = 12\Omega \)
+ Ta đặt, \({R_{MC}} = x\left( \Omega \right)\) với điều kiện \(0 < x < 12\)
\( \Rightarrow {R_{CN}} = 12 - x\left( \Omega \right)\)
+ Điện trở tương đương của mạch: \({R_m} = \dfrac{{{R_D}{R_{CM}}}}{{{R_D} + {R_{CM}}}} + {R_{CN}}\)
\( \Rightarrow {R_m} = \dfrac{{12x}}{{12 + x}} + 12 - x = \dfrac{{12x + 144 - {x^2}}}{{12 + x}}\)
+ Cường độ dòng điện qua mạch: \(I = \dfrac{{{U_{AB}}}}{{{R_m}}} = \dfrac{{15}}{{\dfrac{{12x + 144 - {x^2}}}{{12 + x}}}} = \dfrac{{15\left( {12 + x} \right)}}{{12x + 144 - {x^2}}}\) (1)
+ Vì \({R_{CM}}//{R_D}\) ta suy ra: \({U_{CM}} = {U_D}\)
\(\begin{array}{l} \Leftrightarrow {I_{CM}}{R_{CM}} = {I_D}{R_D}\\ \Leftrightarrow {I_{CM}}.x = {I_D}.12\\ \Rightarrow {I_{CM}} = \dfrac{{12}}{x}{I_D}\end{array}\)
+ Lại có:
\(\begin{array}{l}I = {I_{CM}} + {I_D} \Leftrightarrow I = \dfrac{{12}}{x}{I_D} + {I_D}\\ \Leftrightarrow I = {I_D}\left( {\dfrac{{12}}{x} + 1} \right)\end{array}\)
\( \Rightarrow {I_D} = \dfrac{{xI}}{{12 + x}}\) (2)
Thay (1) vào (2), ta được: \({I_D} = \dfrac{x}{{12 + x}}\left( {\dfrac{{15\left( {12 + x} \right)}}{{12x + 144 - {x^2}}}} \right) = \dfrac{{15x}}{{ - {x^2} + 12x + 144}}\)
Vậy cường độ dòng điện qua đèn phụ thuộc vào \(x\) theo biểu thức: \({I_D} = \dfrac{{15}}{{ - x + 12 + \dfrac{{144}}{x}}}\)
Ta thấy, khi C dịch chuyển về phía A thì x giảm dẫn đến \(\left( { - x + 12 + \dfrac{{144}}{x}} \right)\) tăng lên
\( \Rightarrow {I_D}\) giảm đi
\( \Rightarrow \) Độ sáng của đèn giảm đi (tức đèn sẽ tối dần) khi dịch chuyển con chạy C về A.
Cho mạch điện như hình vẽ:

Khi con chạy C ở vị trí M thì vôn kế chỉ \(12V\). Khi con chạy C ở vị trí N thì vôn kế chỉ \(7,2V\). Tính giá trị của điện trở \(R\), biết trên biến trở có ghi \(20\Omega - 1A\).
Ta có:
+ Khi con chạy C trùng với M thì \({R_{CN}} = 0 \Rightarrow {R_{td}} = R\) và khi đó vôn kế chỉ \(12V\) nghĩa là \({U_{AB}} = 12V\)
+ Khi con chạy C trùng với N thì ta có: \({R_{CN}} = {R_{MN}} = 20\Omega \) (bằng số ghi của biến trở)
Khi đó vôn kế chỉ \(7,2V\)
\( \Rightarrow {U_R} = 7,2V\)
\( \Rightarrow {U_{MN}} = {U_{AB}} - {U_R} = 12 - 7,2 = 4,8V\)
+ Ta có: \({I_{MN}} = \dfrac{{{U_{MN}}}}{{{R_{MN}}}} = \dfrac{{4,8}}{{20}} = 0,24A\)
Vì mạch nối tiếp nên ta có: \({I_R} = {I_{MN}} = 0,24A\)
Suy ra điện trở \(R = \dfrac{{{U_R}}}{{{I_R}}} = \dfrac{{7,2}}{{0,24}} = 30\Omega \)
Một biến trở con chạy được làm bằng dây dẫn hợp kim Nikelin có điện trở suất \({4.10^{ - 7}}\Omega .m\), có tiết diện đầu là \(0,8m{m^2}\) và gồm \(300\) vòng cuốn quanh lõi sứ trụ tròn đường kính \(4,5cm\). Tính điện trở lớn nhất của biến trở này.
Ta có:
+ Chiều dài của một vòng quấn là: \(C = 2\pi R = \pi d = 2\pi .0,045 = 0,1414m\)
+ Chiều dài của toàn bộ dây quấn: \(l = nC = 300.0,1414 = 42,42m\)
+ Điện trở \(R = \rho \dfrac{l}{S} = {4.10^{ - 7}}\dfrac{{42,42}}{{{{0,8.10}^{ - 6}}}} = 21,21\Omega \)
Một biến trở con chạy được làm bằng dây dẫn hợp kim Nikelin có điện trở suất \({4.10^{ - 7}}\Omega .m\), có tiết diện đầu là \(0,8m{m^2}\) và gồm \(300\) vòng cuốn quanh lõi sứ trụ tròn đường kính \(4,5cm\). Hiệu điện thế lớn nhất được phép đặt vào là \(63,585V\). Hỏi biến trở này chịu được dòng điện có cường độ lớn nhất là bao nhiêu?
Ta có:
+ Chiều dài của một vòng quấn là: \(C = 2\pi R = \pi d =\pi .0,045 = 0,1414m\)
+ Chiều dài của toàn bộ dây quấn: \(l = nC = 300.0,1414 = 42,42m\)
+ Điện trở lớn nhất của biến trở là: \(R = \rho \dfrac{l}{S} = {4.10^{ - 7}}\dfrac{{42,42}}{{{{0,8.10}^{ - 6}}}} = 21,21\Omega \)
Ta suy ra, dòng điện lớn nhất mà biến trở chịu được là: \({I_{max}} = \dfrac{{{U_{max}}}}{{{R_{max}}}} = \dfrac{{63,585}}{{21,21}} \approx 3A\)
Dòng điện chạy qua một vòng dây dẫn tại hai điểm A, B. Dây dẫn tạo nên vòng dây là đồng chất, tiết diện đều và có điện trở \({R_0} = 25\Omega \), góc \(AOB = \alpha = {72^0}\). Tính điện trở tương đương của vòng dây khi mắc vào mạch điện tại A và B.
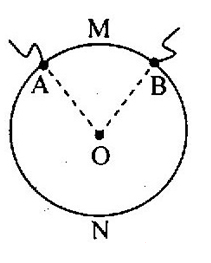
Ta có:
+ Điện trở của cả vòng dây là \({R_0}\)
+ Chiều dài của vòng dây là \(C = 2\pi r\) (với \(r\) là bán kính của vòng tròn)
+ Điện trở của đoạn \(AMB\) là: \({R_{AMB}} = \dfrac{\alpha }{{360}}{R_0}\)
+ Điện trở của đoạn \(ANB\) là: \({R_{ANB}} = \dfrac{{360 - \alpha }}{{360}}{R_0}\)
Mặt khác, ta có: \(AMB//ANB\) nên: \(R = \dfrac{{{R_{AMB}}{R_{ANB}}}}{{{R_{AMB}} + {R_{ANB}}}} = \dfrac{{\left( {360 - \alpha } \right)\alpha }}{{{{360}^2}}}{R_0}\)
Thay \(\left\{ \begin{array}{l}\alpha = {72^0}\\{R_0} = 25\Omega \end{array} \right.\) ta được: \(R = \dfrac{{\left( {360 - 72} \right).72}}{{{{360}^2}}}.25 = 4\Omega \)
Cho mạch điện như hình vẽ.

Biến trở AB là dây đồng chất, có chiều dài \(l = 1,2m\), tiết diện \(S = 0,2m{m^2}\), điện trở suất \({10^{ - 6}}\Omega m\), U- hiệu điện thế không đổi. Nhận thấy khi con chạy ở các vị trí cách đầu A hoặc đầu B những đoạn như nhau bằng \(30cm\) thì công suất tỏa nhiệt trên biến trở là như nhau. Xác định \({R_0}\) ứng với vị trí của C.
Gọi \({R_1},{\rm{ }}{R_2}\) là điện trở của biến trở ứng với 2 vị trí trên của con chạy C; \(R\) là điện trở toàn phần của biến trở.
+ Điện trở toàn phần của biến trở: \(R = \rho \dfrac{l}{S} = {10^{ - 6}}\dfrac{{1,2}}{{{{0,2.10}^{ - 6}}}} = 6\Omega \)
\( \Rightarrow \left\{ \begin{array}{l}{R_1} = \dfrac{3}{{12}}R = 1,5\Omega \\{R_2} = \dfrac{9}{{12}}R = 4,5\Omega \end{array} \right.\)
+ Ta có:
\(\begin{array}{l}{P_1} = {P_2}\\ \Leftrightarrow {\left( {\dfrac{U}{{{R_0} + {R_1}}}} \right)^2}{R_1} = {\left( {\dfrac{U}{{{R_0} + {R_2}}}} \right)^2}{R_2}\\ \Rightarrow {R_0} = \sqrt {{R_1}{R_2}} = \sqrt {1,5.4,5} \approx 2,6\Omega \end{array}\)
Cho mạch điện như hình vẽ:
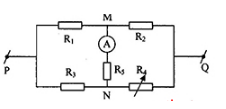
Biết \({R_1} = 0,5\Omega \), \({U_{PQ}} = 4V\), \({R_A} = 0,5\Omega \). Khi \({R_4} = 4\Omega \) thì \({I_A} = 0A\). Tích \({R_2}.{R_3}\) là?
Khi \({R_4} = 4\Omega \) thì \({I_A} = 0\), mạch trở thành mạch cầu cân bằng:
\(\begin{array}{l}\dfrac{{{R_1}}}{{{R_3}}} = \dfrac{{{R_2}}}{{{R_4}}}\\ \Rightarrow {R_2}{R_3} = {R_1}{R_4} = 0,5.4 = 2 \end{array}\)
Mắc vào hai đầu điện trở R một nguồn điện không đổi, có điện trở trong r thì hiệu suất của nguồn điện là 80%. Nếu mắc vào hai đầu điện trở 3R một nguồn điện không đổi, có điện trở trong r’ thì hiệu suất của nguồn là 96%. Tỉ số \(\frac{r}{{r'}}\) là
+ Khi mắc vào mạch điện một điện trở R thì:
\({H_1} = \dfrac{R}{{R + r}} = 0,8 \Rightarrow r = \dfrac{R}{4}\,\,\,\left( 1 \right)\)
+ Khi mắc vào mạch điện một điện trở 3R thì:
\({H_2} = \dfrac{{3R}}{{3{\rm{R}} + r'}} = 0,96 \Rightarrow r' = \dfrac{R}{8}\,\,\,\left( 2 \right)\)
Từ (1) và (2) ta suy ra: \(\dfrac{r}{{r'}} = \dfrac{{\dfrac{R}{4}}}{{\dfrac{R}{8}}} = 2\)
Đặt vào hai đầu AB của một đoạn dây dẫn đồng chất, tiết diện đều một hiệu điện thế U. Tỉ số các hiệu điện thế UAC và UCB là bao nhiêu? Biết điểm C chia đoạn AB theo tỉ lệ AC/AB = 4/5

Bài toán tương đương với điện trở RAC nối tiếp với điện trở RCB nên IAC = ICB
Do đó, ta có:
\(\frac{{{U_{AC}}}}{{{U_{CB}}}} = \frac{{{I_{AC}}{R_{AC}}}}{{{I_{CB}}{R_{CB}}}} = \frac{{{R_{AC}}}}{{{R_{CB}}}}\)
Mặt khác, ta có: \(R = \rho \frac{l}{S}\)
\(\frac{{{U_{AC}}}}{{{U_{CB}}}} = \frac{{{R_{AC}}}}{{{R_{CB}}}} = \frac{{{l_{AC}}}}{{{l_{CB}}}} = \frac{{AC}}{{CB}} = \frac{{AC}}{{AB - AC}}\)
Theo đề bài, ta có:
\(\frac{{AC}}{{AB}} = \frac{4}{5} \to AB = 1,25AC\)
\( \to \frac{{{U_{AC}}}}{{{U_{CB}}}} = \frac{{AC}}{{AB - AC}} = \frac{{AC}}{{1,25AC - AC}} = 4\)
Một dây nhôm dạng hình trụ tròn được quấn thành cuộn có khối lượng 0,81kg. Tiết diện thẳng của dây là 0,1mm2. Tìm điện trở của dây đó biết rằng nhôm có khối lượng riêng và điện trở suất lần lượt là 2,7g/cm3 và 2,8.10-8$\Omega $m?
+ Thể tích của cuộn dây:
\(V = \frac{m}{D} = \frac{{0,81}}{{2,{{7.10}^3}}} = {3.10^{ - 4}}{m^3}\)
+ Chiều dài của dây nhôm:
\(l = \frac{V}{S} = \frac{{{{3.10}^{ - 4}}}}{{0,{{1.10}^{ - 6}}}} = 3000m\)
+ Điện trở của cuộn dây nhôm:
\(R = \rho \frac{l}{S} = 2,{8.10^{ - 8}}\frac{{3000}}{{0,{{1.10}^{ - 6}}}} = 840\Omega \)
Cho mạch điện như hình vẽ:
Đ(24V - 0,8A), hiệu điện thế giữa hai điểm A và B được giữ không đổi U = 32V
Biết đèn sáng bình thường, điện trở của biến trở khi đó là?
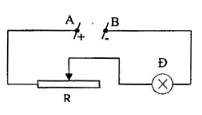
Vì đèn sáng bình thường nên dòng điện chạy trong mạch là: I = 0,8A
Ta có:
+ Điện trở của bóng đèn:
\({R_D} = \frac{{{U_D}}}{{{I_D}}} = \frac{{24}}{{0,8}} = 30\Omega \)
+ Điện trở của mạch:
\({R_{AB}} = \frac{{{U_{AB}}}}{I} = \frac{{32}}{{0,8}} = 40\Omega \)
Mặt khác, ta có: Biến trở mắc nối tiếp với bóng đèn:
RAB = RD + R => R = RAB - RD = 40 - 30 = 10$\Omega $
Cho mạch điện như hình vẽ:
Đ(24V - 0,8A), hiệu điện thế giữa hai điểm A và B được giữ không đổi U = 32V
Dịch chuyển con chạy của biến trở sao cho điện trở của biến trở R’ = 20$\Omega $. Cường độ bóng đèn như thế nào?
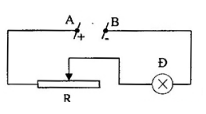
Ta có:
+ Điện trở của bóng đèn:
\({R_D} = \frac{{{U_D}}}{{{I_D}}} = \frac{{24}}{{0,8}} = 30\Omega \)
+ Điện trở của biến trở: R’ = 20$\Omega $
+ Điện trở của mạch: RAB = RD + R’ = 30 + 20 = 50$\Omega $
+ Cường độ dòng điện trong mạch khi này:
\(I = \frac{U}{{{R_{AB}}}} = \frac{{32}}{{50}} = 0,64A\)
Đèn sáng bình thường khi cường độ dòng điện trong mạch là 0,8A
Ta thấy I < 0,8A => Đèn sáng yếu hơn mức bình thường
Cho mạch điện như hình vẽ:
Trên bóng đèn Đ có ghi 6V - 0,75A. Đèn được mắc với biến trở, biết rằng trên biến trở có ghi (16$\Omega $ - 1A) và UAB không đổi bằng 12V. Tính RCN của biến trở để đèn sáng bình thường?
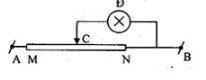
Sơ đồ mạch điện được vẽ lại như hình
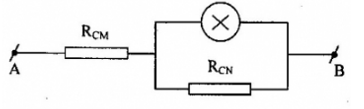
+ Vì điện trở lớn nhất của biến trở (điện trở toàn phần của biến trở là 16$\Omega $), nên ta có:
RCN = R1 thì RCM = 16 - R1
+ Đèn sáng bình thường nên: UD = 6V = UCN
\( \to {I_{CN}} = \frac{{{U_{CN}}}}{{{R_1}}} = \frac{6}{{{R_1}}}\)
Mặt khác, ta có:
\({I_{CM}} = {\text{ }}{I_{CN}} + {\text{ }}{I_D} \leftrightarrow \frac{6}{{16 - {R_1}}} = \frac{6}{{{R_1}}} + 0,75\)
\( \leftrightarrow 0,75R_1^2 = 96 \to {R_1} = 8\sqrt 2 \)
Một cuộn dây dẫn bằng đồng có khối lượng 1,068kg, dây dẫn có tiết diện 1mm2. Biết điện trở suất của đồng là 1,7.10-8$\Omega $m, khối lượng riêng của đồng là 8900kg/m3. Người ta dùng dây này để cuốn một biến trở hình trụ tròn đường kính 2cm. Số vòng dây quấn của biến trở là bao nhiêu?
Ta có:
+ Thể tích của cuộn dây:
\(V = \frac{m}{D} = \frac{{1,068}}{{8,{{9.10}^3}}} = 1,{2.10^{ - 4}}{m^3}\)
+ Chiều dài của dây đồng:
\(l = \frac{V}{S} = \frac{{1,{{2.10}^{ - 4}}}}{{{{10}^{ - 6}}}} = 120m\)
+ Chiều dài của một vòng quấn là:
\(C = 2\pi R = \pi d = \pi .0,02 = 0,0628m\)
=> Số vòng dây quấn:
\(n = \frac{l}{C} = \frac{{120}}{{0,0628}} = 1909,9 \approx 1910\) vòng
Một biến trở con chạy có điện trở lớn nhất là 150$\Omega $. Dây điện trở của biến trở là một hợp kim nicrom có tiết diện 0,11mm2 và được quấn đều xung quanh một lõi sứ tròn có đường kính 2,5cm. Biết điện trở suất của nicrom là 1,1.10-6$\Omega $m, dòng điện lớn nhất mà dây có thể chịu được là 2A. Ta có thể đặt vào hai đầu dây này một hiệu điện thế lớn nhất là bao nhiêu để biến trở không bị hỏng?
Điện trở lớn nhất của biến trở là R0 = 150$\Omega $ nên hiệu điện thế lớn nhất có thể đặt vào biến trở là:
Umax = Imax R0 = 2.150 = 300V

