Câu hỏi:
2 năm trước
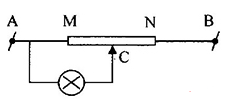
Đặt vào hai đầu AB của một đoạn dây dẫn đồng chất, tiết diện đều một hiệu điện thế U. Tỉ số các hiệu điện thế UAC và UCB là bao nhiêu? Biết điểm C chia đoạn AB theo tỉ lệ AC/AB = 4/5
Trả lời bởi giáo viên
Đáp án đúng: a
Bài toán tương đương với điện trở RAC nối tiếp với điện trở RCB nên IAC = ICB
Do đó, ta có:
\(\frac{{{U_{AC}}}}{{{U_{CB}}}} = \frac{{{I_{AC}}{R_{AC}}}}{{{I_{CB}}{R_{CB}}}} = \frac{{{R_{AC}}}}{{{R_{CB}}}}\)
Mặt khác, ta có: \(R = \rho \frac{l}{S}\)
\(\frac{{{U_{AC}}}}{{{U_{CB}}}} = \frac{{{R_{AC}}}}{{{R_{CB}}}} = \frac{{{l_{AC}}}}{{{l_{CB}}}} = \frac{{AC}}{{CB}} = \frac{{AC}}{{AB - AC}}\)
Theo đề bài, ta có:
\(\frac{{AC}}{{AB}} = \frac{4}{5} \to AB = 1,25AC\)
\( \to \frac{{{U_{AC}}}}{{{U_{CB}}}} = \frac{{AC}}{{AB - AC}} = \frac{{AC}}{{1,25AC - AC}} = 4\)
Hướng dẫn giải:
+ Áp dụng biểu thức xác định hiệu điện thế: U = IR
+ Áp dụng biểu thức xác định điện trở của dây dẫn: \(R = \rho \frac{l}{S}\)
Câu hỏi khác
- Bài tập điện năng và công suất điện - định luật jun- lenxơ lý 11 có lời giải
- Bài tập định luật ôm đối với toàn mạch - mắc nguồn điện thành bộ lý 11 có lời giải
- Bài tập tính điện trở dây dẫn - biến trở có lời giải MÔN LÝ lớp 11
- Bài tập định luật ôm cho đoạn mạch chỉ có điện trở lý 11 có lời giải
- Bài tập đại cương về dòng điện không đổi - nguồn điện lý 11 có lời giải.
