Câu hỏi:
2 năm trước
Cho mạch điện như hình vẽ:
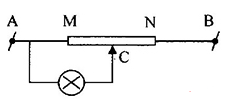
Biết trở có điện trở toàn phần \({R_0} = 12\Omega \), đèn Đ có ghi \(6V - 3W\), \({U_{AB}} = 15V\). Điện trở \({R_{CM}} = ?\) để đèn sáng bình thường.
Trả lời bởi giáo viên
Đáp án đúng: d
+ Mạch điện được vẽ lại như hình:
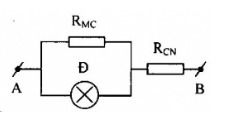
+ Ta đặt, \({R_{MC}} = x\left( \Omega \right)\) với điều kiện \(0 < x < 12\)
\( \Rightarrow {R_{CN}} = 12 - x\left( \Omega \right)\)
+ Khi đèn sáng bình thường, cường độ dòng điện qua đèn \({I_D} = \dfrac{{{P_D}}}{{{U_D}}} = \dfrac{3}{6} = 0,5W\)
+ Ta có \(\left[ {D//{R_{CM}}} \right]nt{R_{CN}}\) nên:
\({U_{CM}} = {U_D} = 6V\)
\({U_{CN}} = {U_{AB}} - {U_D} = 15 - 6 = 9V\)
+ Mặt khác, ta có: \({I_{CN}} = {I_{CM}} + {I_D}\) (1)
Trong đó: \(\left\{ \begin{array}{l}{I_D} = 0,5\\{I_{CM}} = \dfrac{{{U_{CM}}}}{{{R_{CM}}}} = \dfrac{6}{x}\\{I_{CN}} = \dfrac{{{U_{CN}}}}{{{R_{CN}}}} = \dfrac{9}{{12 - x}}\end{array} \right.\)
Ta suy ra: \(\left( 1 \right) \Leftrightarrow \dfrac{9}{{12 - x}} = \dfrac{6}{x} + 0,5\)
\(\begin{array}{l} \Leftrightarrow 0,5{x^2} + 9x - 72 = 0\\ \Rightarrow \left[ \begin{array}{l}x = 6\Omega \\x = - 24\Omega \left( {loai} \right)\end{array} \right.\end{array}\)
Vậy với \({R_{CM}} = 6\Omega \) thì khi đó đèn sáng bình thường.
Hướng dẫn giải:
+ Vẽ lại mạch điện
+ Sử dụng biểu thức \(P = UI\)
+ Vận dụng biểu thức định luật ôm: \(I = \dfrac{U}{R}\)
+ Vận dụng biểu thức tính cường độ dòng điện của đoạn mạch mắc nối tiếp
Câu hỏi khác
- Bài tập điện năng và công suất điện - định luật jun- lenxơ lý 11 có lời giải
- Bài tập định luật ôm đối với toàn mạch - mắc nguồn điện thành bộ lý 11 có lời giải
- Bài tập tính điện trở dây dẫn - biến trở có lời giải MÔN LÝ lớp 11
- Bài tập định luật ôm cho đoạn mạch chỉ có điện trở lý 11 có lời giải
- Bài tập đại cương về dòng điện không đổi - nguồn điện lý 11 có lời giải.
