Cho đoạn mạch gồm R1 mắc nối tiếp với R2, biểu thức nào sau đây là đúng?
A – sai vì: khi \({R_1}\) mắc nối tiếp với \({R_2}\) thì \(R = {R_1} + {R_2}\)
B – sai vì: khi \({R_1}\) mắc nối tiếp với \({R_2}\) thì \(U = {U_1} + {U_2}\)
C - sai vì : khi \({R_1}\) mắc nối tiếp với \({R_2}\) thì \(I = {I_1} = {I_2}\)
D - đúng
Cho đoạn mạch gồm \({R_1}\) mắc song song với \({R_2}\), biểu thức nào sau đây là sai?
Khi \({R_1}\) mắc song song với \({R_2}\) ta có:
\(\begin{array}{l}\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} \to R = \dfrac{{{R_1}{R_2}}}{{{R_1} + {R_2}}}\\U = {U_1} = {U_2}\\I = {I_1} + {I_2}\\{I_1} = \dfrac{{{U_1}}}{{{R_1}}}\end{array}\)
Ta suy ra, các phương án:
A, C, D - đúng
B - sai
Cho mạch điện như hình vẽ
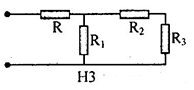
Tính điện trở tương đương của toàn mạch biết các điện trở đều bằng nhau và bằng \(R = 12\Omega \).
Từ mạch điện ta có: \(\left( {\left[ {{R_2}nt{R_3}} \right]//{R_1}} \right)ntR\)
+ Ta có \({R_2}nt{R_3}\) suy ra: \({R_{23}} = {R_2} + {R_3} = 12 + 12 = 24\Omega \)
+ \({R_{23}}//{R_1}\) suy ra: \(\dfrac{1}{{{R_{123}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_{23}}}} \Rightarrow {R_{123}} = \dfrac{{{R_1}{R_{23}}}}{{{R_1} + {R_{23}}}} = \dfrac{{12.24}}{{12 + 24}} = 8\Omega \)
+ \({R_{123}}ntR\) suy ra: \({R_{td}} = R + {R_{123}} = 12 + 8 = 20\Omega \)
Cho mạch điện như hình vẽ
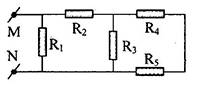
Tính điện trở tương đương của mạch điện. Biết \({R_1} = 1\Omega ;{R_2} = 2,4\Omega \),\({R_3} = 2\Omega ,{R_4} = 5\Omega \), \({R_5} = 3\Omega \)
Từ mạch điện ta thấy: \(\left[ {\left( {\left[ {{R_4}nt{R_5}} \right]//{R_3}} \right)nt{R_2}} \right]//{R_1}\)
Ta có:
+ \({R_4}nt{R_5}\) suy ra: \({R_{45}} = {R_4} + {R_5} = 5 + 3 = 8\Omega \)
+ \({R_{45}}//{R_3}\) suy ra: \(\dfrac{1}{{{R_{345}}}} = \dfrac{1}{{{R_3}}} + \dfrac{1}{{{R_{45}}}} \Rightarrow {R_{345}} = \dfrac{{{R_3}{R_{45}}}}{{{R_3} + {R_{45}}}} = \dfrac{{2.8}}{{2 + 8}} = 1,6\Omega \)
+ \({R_{345}}nt{R_2}\) suy ra: \({R_{2345}} = {R_2} + {R_{345}} = 2,4 + 1,6 = 4\Omega \)
+ \({R_{2345}}//{R_1}\) suy ra: \(\dfrac{1}{{{R_{td}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_{2345}}}} \Rightarrow {R_{td}} = \dfrac{{{R_1}{R_{2345}}}}{{{R_1} + {R_{2345}}}} = \dfrac{{1.4}}{{1 + 4}} = 0,8\Omega \)
Vậy điện trở tương đương của toàn mạch là \({R_{td}} = 0,8\Omega \)
Cho mạch điện như hình vẽ
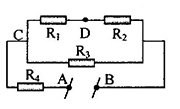
Biết \({R_1} = 1\Omega ;\) \({R_2} = {R_3} = 2\Omega ;\) \({R_4} = 0,8\Omega \)\(U = 6V\)
Cường độ dòng điện chạy qua mạch AB là:
Từ mạch điện, ta thấy : \(\left[ {\left[ {{R_1}nt{R_2}} \right]//{R_3}} \right]nt{R_4}\)
Ta có:
+ \({R_1}nt{R_2}\) suy ra: \({R_{12}} = {R_1} + {R_2} = 1 + 2 = 3\Omega \)
+ \({R_{12}}//{R_3}\) suy ra: \(\dfrac{1}{{{R_{123}}}} = \dfrac{1}{{{R_{12}}}} + \dfrac{1}{{{R_3}}} \Rightarrow {R_{123}} = \dfrac{{{R_{12}}.{R_3}}}{{{R_{12}} + {R_3}}} = \dfrac{{3.2}}{{3 + 2}} = 1,2\Omega \)
+ \({R_{123}}nt{R_4}\) suy r: \({R_{td}} = {R_{123}} + {R_4} = 1,2 + 0,8 = 2\Omega \)
Cường độ dòng điện trong mạch: \(I = \dfrac{U}{{{R_{td}}}} = \dfrac{6}{2} = 3A\)
Cho mạch điện như hình vẽ
+ Ta thấy: \(\left[ {\left( {{R_2}nt{R_4}} \right)//{R_1}} \right]nt{R_3}\)
\({R_{24}} = {R_2} + {R_4} = 2 + 6 = 8\Omega \)
\(\dfrac{1}{{{R_{124}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_{24}}}} \Rightarrow {R_{124}} = \dfrac{{{R_1}{R_{24}}}}{{{R_1} + {R_{24}}}} = \dfrac{{2.8}}{{2 + 8}} = 1,6\Omega \)
\({R_{td}} = {R_{3124}} = {R_3} + {R_{124}} = 2 + 1,6 = 3,6\Omega \)
+ Cường độ dòng điện qua mạch chính: \(I = \dfrac{U}{{{R_{td}}}} = \dfrac{{7,2}}{{3,6}} = 2A\)
Ta có: \({U_{MB}} = U - {U_{AM}} = U - I.{R_3} = 7,2 - 2.2 = 3,2A\)
Lại có: \({U_{MB}} = {I_2}.{R_{24}} \Rightarrow {I_2} = \dfrac{{{U_{MB}}}}{{{R_{24}}}} = \dfrac{{3,2}}{8} = 0,4A\)
Vậy số chỉ của ampe kế là \(0,4A\)
Cho mạch điện như hình vẽ
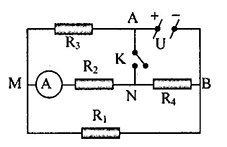
\({U_{AB}} = 7,2V\) không đổi, \({R_1} = {R_2} = {R_3} = 2\Omega ;\) \({R_4} = 6\Omega \). Điện trở của ampe kế và khóa K không đáng kể. Tìm số chỉ của ampe kế khi khóa K mở
+ Khi khóa K mở, mạch được vẽ lại như hình:
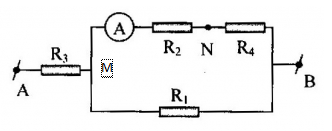
+ Ta thấy: \(\left[ {\left( {{R_2}nt{R_4}} \right)//{R_1}} \right]nt{R_3}\)
\({R_{24}} = {R_2} + {R_4} = 2 + 6 = 8\Omega \)
\(\dfrac{1}{{{R_{124}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_{24}}}} \Rightarrow {R_{124}} = \dfrac{{{R_1}{R_{24}}}}{{{R_1} + {R_{24}}}} = \dfrac{{2.8}}{{2 + 8}} = 1,6\Omega \)
\({R_{td}} = {R_{3124}} = {R_3} + {R_{124}} = 2 + 1,6 = 3,6\Omega \)
+ Cường độ dòng điện qua mạch chính: \(I = \dfrac{U}{{{R_{td}}}} = \dfrac{{7,2}}{{3,6}} = 2A\)
Ta có: \({U_{MB}} = U - {U_{AM}} = U - I.{R_3} = 7,2 - 2.2 = 3,2A\)
Lại có: \({U_{MB}} = {I_2}.{R_{24}} \Rightarrow {I_2} = \dfrac{{{U_{MB}}}}{{{R_{24}}}} = \dfrac{{3,2}}{8} = 0,4A\)
Vậy số chỉ của ampe kế là \(0,4A\)
Cho mạch điện như hình vẽ
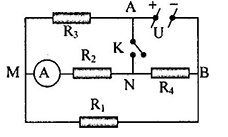
\({U_{AB}} = 7,2V\) không đổi, \({R_1} = {R_2} = {R_3} = 2\Omega ;\) \({R_4} = 6\Omega \). Điện trở của ampe kế và khóa K không đáng kể. Tìm \({U_{AN}}\) khi khóa K mở
+ Khi khóa K mở, mạch được vẽ lại như hình:
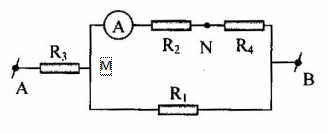
+ Ta thấy: \(\left[ {\left( {{R_2}nt{R_4}} \right)//{R_1}} \right]nt{R_3}\)
\({R_{24}} = {R_2} + {R_4} = 2 + 6 = 8\Omega \)
\(\dfrac{1}{{{R_{124}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_{24}}}} \Rightarrow {R_{124}} = \dfrac{{{R_1}{R_{24}}}}{{{R_1} + {R_{24}}}} = \dfrac{{2.8}}{{2 + 8}} = 1,6\Omega \)
\({R_{td}} = {R_{3124}} = {R_3} + {R_{124}} = 2 + 1,6 = 3,6\Omega \)
+ Cường độ dòng điện qua mạch chính: \(I = \dfrac{U}{{{R_{td}}}} = \dfrac{{7,2}}{{3,6}} = 2A\)
Ta có: \({U_{MB}} = U - {U_{AM}} = U - I.{R_3} = 7,2 - 2.2 = 3,2A\)
Lại có: \({U_{MB}} = {I_2}.{R_{24}} \Rightarrow {I_2} = \dfrac{{{U_{MB}}}}{{{R_{24}}}} = \dfrac{{3,2}}{8} = 0,4A\)
Ta có: \({U_{AN}} = {U_{AM}} + {U_{MN}} = {U_3} + {U_2} = I.{R_3} + {I_2}.{R_2} = 2.2 + 0,4.2 = 4,8V\)
Cho mạch điện như hình vẽ:
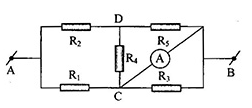
\({U_{AB}} = 24V\), \({R_1} = {R_2} = {R_3} = {R_4} = {R_5} = 10\Omega \)
Điện trở tương đương của toàn mạch có giá trị là
Vì ampe kế có điện trở không đáng kể nên B và C có cùng điện thế
\( \Rightarrow \) chập C và B lại. Vẽ lại mạch điện như hình sau:
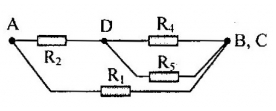
Ta có: \(\left[ {\left( {{R_4}//{R_5}} \right)nt{R_2}} \right]//{R_1}\)
Suy ra:
\({R_{45}} = \dfrac{{{R_4}{R_5}}}{{{R_4} + {R_5}}} = \dfrac{{10.10}}{{10 + 10}} = 5\Omega \)
\({R_{245}} = {R_2} + {R_{45}} = 10 + 5 = 15\Omega \)
\({R_{AB}} = {R_{1245}} = \dfrac{{{R_1}{R_{245}}}}{{{R_1} + {R_{245}}}} = \dfrac{{10.15}}{{10 + 15}} = 6\Omega \)
Cho mạch điện như hình vẽ:
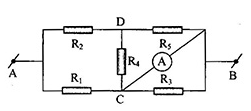
\({U_{AB}} = 24V\), \({R_1} = {R_2} = {R_3} = {R_4} = {R_5} = 10\Omega \)
Tính số chỉ của ampe kế?
Vì ampe kế có điện trở không đáng kể nên B và C có cùng điện thế
\( \Rightarrow \) chập C và B lại. Vẽ lại mạch điện như hình sau:
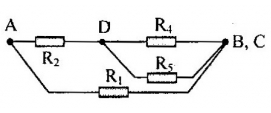
Ta có: \(\left[ {\left( {{R_4}//{R_5}} \right)nt{R_2}} \right]//{R_1}\)
Suy ra:
\({R_{45}} = \dfrac{{{R_4}{R_5}}}{{{R_4} + {R_5}}} = \dfrac{{10.10}}{{10 + 10}} = 5\Omega \)
\({R_{245}} = {R_2} + {R_{45}} = 10 + 5 = 15\Omega \)
\({R_{AB}} = {R_{1245}} = \dfrac{{{R_1}{R_{245}}}}{{{R_1} + {R_{245}}}} = \dfrac{{10.15}}{{10 + 15}} = 6\Omega \)
(Để tìm số chỉ ampe kế A ta phải tìm \({I_1}\) và \({I_4}\) sau đó xác định chiều của \({I_4}\) rồi suy ra số chỉ của A)
+ Ta có: \({U_{245}} = {U_1} = {U_{AB}} = 24V\)
+ Dòng điện chạy qua đoạn \({R_1}\): \({I_1} = \dfrac{U}{{{R_1}}} = \dfrac{{24}}{{10}} = 2,4A\)
+ Dòng điện chạy qua đoạn \({R_2} - {R_{45}}\): \({I_{2 - 45}} = \dfrac{U}{{{R_{245}}}} = \dfrac{{24}}{{15}} = 1,6A\)
Lại có, \({I_2} = {I_{45}} = {I_{2 - 45}} = 1,6A\) nên \({U_{45}} = {U_{AB}} - {U_2} = {U_{AB}} - {I_2}{R_2} = 24 - 1,6.10 = 8V\)
Vì \({U_4} = {U_5} = {U_{45}} = 8V\) mà \({R_4} = {R_5} = 10\Omega \)
\( \Rightarrow {I_4} = {I_5} = \dfrac{{{U_{45}}}}{{{R_4}}} = \dfrac{8}{{10}} = 0,8A\)
Dựa vào mạch gốc, ta thấy tại D có \({I_2} > {I_5}\) nên dòng qua \({I_4}\) phải có chiều từ D đến C vậy \({I_1}\) và \({I_4}\) chạy qua A nên:
\({I_A} = {I_1} + {I_4} = 2,4 + 0,8 = 3,2A\)
Cho mạch điện như hình vẽ:
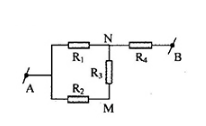
\({R_1} = {\rm{ }}{R_2} = {\rm{ }}{R_3} = 3\Omega ,{\rm{ }}{R_4} = 6\Omega .\) Tính điện trở tương đương của mạch khi ta nối M và B bằng một ampe kế có điện trở rất nhỏ?
Vì ampe kế có điện trở rất nhỏ nên M và B cùng điện thế
=> chập M và B mạch điện được vẽ lại như hình
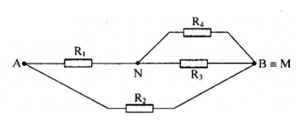
Ta có: \({R_2}//{\rm{ }}[\left( {{R_1}nt{\rm{ }}\left( {{R_3}//{R_4}} \right)} \right]\)
\(\begin{array}{l}\dfrac{1}{{{R_{34}}}} = \dfrac{1}{{{R_3}}} + \dfrac{1}{{{R_4}}}\\ \to {R_{34}} = \dfrac{{{R_3}{R_4}}}{{{R_3} + {R_4}}} = \dfrac{{3.6}}{{3 + 6}} = 2\Omega \end{array}\)
\({R_{134}} = {R_1} + {R_{34}} = 3 + 2 = 5\Omega \)
Điện trở tương đương của toàn mạch: \(\dfrac{1}{R} = \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_{134}}}} \to R = \dfrac{{{R_2}{R_{134}}}}{{{R_2} + {R_{134}}}} = \dfrac{{3.5}}{{3 + 5}} = \dfrac{{15}}{8}\Omega \)
Cho mạch điện như hình vẽ:
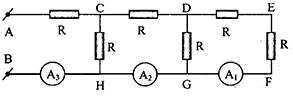
Ampe kế \({A_1}\), \({A_2}\), \({A_3}\) có cùng điện trở \({R_A}\), các điện trở \(R\) có cùng giá trị. Biết rằng ampe kế \({A_1}\) chỉ \(0,2A\), ampe kế \({A_2}\) chỉ \(0,8A\). Hỏi ampe kế \({A_3}\) chỉ bao nhiêu?
Vẽ lại mạch điện ta được:

Ta có:
+ \({I_{DRG}} = {I_{{A_2}}} - {I_{{A_1}}} = 0,8 - 0,2 = 0,6A\)
Lại có: \({U_{DG}} = 0,6R = 0,2\left( {2R + {R_A}} \right)\)
\(\begin{array}{l} \Leftrightarrow 2R + {R_A} = 3R\\ \Rightarrow {R_A} = R\end{array}\)
Mặt khác, \({U_{CH}} = {I_{CRH}}.R = {I_{{A_2}}}\left( {R + \dfrac{{\left( {2R + R} \right)R}}{{\left( {2R + R} \right) + R}} + {R_A}} \right)\)
\(\begin{array}{l} \Leftrightarrow {I_{CRH}}.R = {I_{{A_2}}}\left( {R + \dfrac{{\left( {2R + R} \right)R}}{{\left( {2R + R} \right) + R}} + {R_A}} \right)\\ \Rightarrow {I_{CRH}} = 0,8.2,75 = 2,2A\end{array}\)
+ Số chỉ của ampe kế \({A_3}\) là: \({I_3} = {I_2} + {I_{CRH}} = 0,8 + 2,2 = 3A\)
Có \(50\) điện trở, gồm 3 loại \(1\Omega ;3\Omega \) và \(8\Omega \). Cách chọn số điện trở mỗi loại sao cho khi ghép nối tiếp ta được điện trở tổng cộng \(100\Omega \) là:
Gọi \(x,y,z\) lần lượt là số điện trở loại \(1\Omega ,3\Omega \) và \(8\Omega \)
Với \(x,y,z\) là các số nguyên không âm
Theo đề bài ta có: \(\left\{ \begin{array}{l}x + 3y + 8z = 100{\rm{ }}\left( 1 \right)\\x + y + z = 50{\rm{ }}\left( 2 \right)\end{array} \right.\)
+ Lấy \(\left( 1 \right) - \left( 2 \right)\) ta có: \(2y + 7z = 50 \Rightarrow y = 25 - \dfrac{7}{2}z\)
+ Vì \(y \ge 0 \Rightarrow 25 - \dfrac{7}{2}z \ge 0 \Rightarrow z \le 7,1\) (3)
Để y là số nguyên, không âm thì \(z\) phải là bội của 2 hoặc \(y = 0\) và thỏa mãn điều kiện (3)
Vậy: \(z = 0\) thì \(y = 25 \Rightarrow x = 25\) hoặc \(z = 2\) thì \(y = 18 \Rightarrow x = 30\) hoặc \(z = 4\) thì \(y = 11 \Rightarrow x = 35\), hoặc \(z = 6\) thì \(y = 4 \Rightarrow x = 40\)
Cho \(2013\) ampe kế không lý tưởng; \(2013\) vôn kế giống nhau không lí tưởng mắc như hình, ampe kế \({A_1}\) chỉ \(2A\); ampe kế \({A_2}\) chỉ \(1,5A\), vôn kế \({V_1}\) chỉ \(503,5V\). Hãy tìm tổng số chỉ của \(2013\) vôn kế trong mạch.
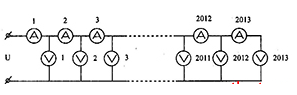
+ Từ mạch điện, ta có: dòng điện qua vôn kế \({V_1}\) là: \(I = {I_{{A_1}}} - {I_{{A_2}}} = 2 - 1,5 = 0,5A\)
+ Điện trở của mỗi vôn kế: \({R_V} = \dfrac{{{U_1}}}{{{I_1}}} = \dfrac{{503,5}}{{0,5}} = 1007\Omega \) (1)
+ Từ mạch điện ta có: \(\left\{ \begin{array}{l}{I_{{A_1}}} = {I_{{A_2}}} + \dfrac{{{U_1}}}{{{R_V}}}\\{I_{{A_2}}} = {I_{{A_3}}} + \dfrac{{{U_2}}}{{{R_V}}}\\.......\\{I_{{A_{2012}}}} = {I_{{A_{2013}}}} + \dfrac{{{U_{2012}}}}{{{R_V}}}\\{I_{{A_{2013}}}} = {I_{V2013}}\end{array} \right.\)
+ Cộng vế với vế của các phương trình trên, ta có:
\({I_{{A_1}}} = {I_{V2013}} + \dfrac{{{U_{2012}}}}{{{R_V}}} + \dfrac{{{U_{2011}}}}{{{R_V}}} + ... + \dfrac{{{U_2}}}{{{R_V}}} + \dfrac{{{U_1}}}{{{R_V}}}\)
\( \Rightarrow {I_{{A_1}}}{R_V} = {I_{V2013}}{R_V} + {U_{2012}} + {U_{2011}} + ... + {U_2} + {U_1}\)
\( \Rightarrow {I_{{A_1}}}{R_V} = {U_{2013}} + {U_{2012}} + {U_{2011}} + ... + {U_2} + {U_1}\) (2)
+ Từ (1) và (2), ta suy ra:
\({U_1} + {U_2} + {U_3} + ... + {U_{2013}} = {I_{{A_1}}}{R_V} = 2.1007 = 2014V\)
Cho mạch điện như hình vẽ: \({R_2} = 6\Omega \),\({U_{MN}} = 45V\). Biết khi \({K_1}\) đóng, \({K_2}\) mở ampe kế chỉ \(1,5A\). Khi \({K_1}\) mở, \({K_2}\) đóng thì ampe kế A chỉ \(3A\). Số chỉ của ampe kế A khi cả 2 khóa \({K_1}\) và \({K_2}\) cùng đóng là?
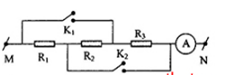
Khi \({K_1}\) đóng còn \({K_2}\) mở thì mạch chỉ có \({R_3}\) \( \to {R_3} = \dfrac{{45}}{{1,5}} = 30\Omega \)
Khi \({K_2}\) đóng, \({K_1}\) mở thì mạch chỉ có \({R_1}\) \( \to {R_1} = \dfrac{{45}}{3} = 15\Omega \)
Khi \({K_1}\) và \({K_2}\) cùng đóng thì : \({R_1}//{\rm{ }}{R_2}//{\rm{ }}{R_3}\):
Điện trở tương đương của mạch:
\(\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} = \dfrac{1}{{15}} + \dfrac{1}{6} + \dfrac{1}{{30}} = \dfrac{1}{5} \to R = 3,75\Omega \)
Ta có, số chỉ ampe kế chính là I mạch chính: \(I = \dfrac{{{U_{MN}}}}{R} = \dfrac{{45}}{{3,75}} = 12A\)
Cho mạch điện như hình vẽ:
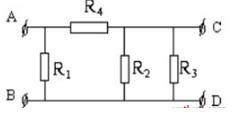
Biết \({R_3} = {\rm{ }}{R_4}\) . Nếu nối hai đầu AB vào hiệu điện thế \(220V\) thì cường độ dòng điện qua \({R_2}\) là \(5A\) và \({U_{CD}} = 40V\). Nếu nối hai đầu CD vào hiệu điện thế \(220V\) thì \({U_{AB}} = {\rm{ }}20V.\) \({R_1}\) có giá trị là?
+ Trường hợp hiệu điện thế đặt vào AB
Mạch gồm: \({R_1}//{\rm{ }}\left[ {{\rm{ }}{R_4}nt{\rm{ }}\left( {{R_3}//{\rm{ }}{R_2}} \right)} \right]\)
Ta có: \({U_{AC}} = {\rm{ }}{U_{AB}} - {\rm{ }}{U_{CD}} = 220 - 40{\rm{ }} = 180V\)
\(\begin{array}{l}{R_3} = {\rm{ }}{R_4}\\ \Rightarrow {I_4} = \dfrac{{{U_{AC}}}}{{{R_4}}} = \dfrac{{180}}{{{R_4}}} = \dfrac{{180}}{{{R_3}}} = {I_2} + {I_3} = 5 + \dfrac{{40}}{{{R_3}}}\\ \Rightarrow {R_3} = {R_4} = 28\Omega \end{array}\)
+ Trường hợp hiệu điện thế đặt vào CD
Mạch gồm \({R_3}//{\rm{ }}\left[ {{\rm{ }}{R_2}//{\rm{ }}\left( {{R_1}nt{\rm{ }}{R_4}} \right)} \right]\)
\( \Rightarrow {U_{AC}} = {\rm{ }}{U_{CD}} - {\rm{ }}{U_{AB}} = {\rm{ }}220 - 40 = 180V\)
\({I_4} = {I_1} = \dfrac{{{U_{AC}}}}{{{R_4}}} = \dfrac{{180}}{{28}} = \dfrac{{47}}{5}A\)
\({R_1} = \dfrac{{{U_{AB}}}}{{{I_1}}} = \dfrac{{180}}{{20}} = 9\Omega \)
Cho mạch điện gồm nguồn điện có \(E = 24\,\,V;\,\,r = 2\,\,\Omega \), mạch ngoài gồm điện trở \(R = 13\,\,\Omega \) mắc nối tiếp với một ampe kế có \({R_A} = 1\,\,\Omega \). Số chỉ của ampe kế là
Số chỉ của Ampe kế là:
\(I = \dfrac{E}{{r + R + {R_A}}} = \dfrac{{24}}{{2 + 13 + 1}} = 1,5\,\,\left( A \right)\)
Cho mạch điện như hình vẽ
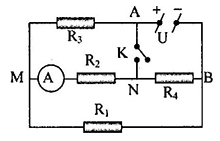
\({U_{AB}} = 7,2V\) không đổi, \({R_1} = {R_2} = {R_3} = 2\Omega ;\) \({R_4} = 6\Omega \). Điện trở của ampe kế và khóa K không đáng kể. Tìm \({U_{AN}}\) khi khóa K mở
+ Khi khóa K mở, mạch được vẽ lại như hình:
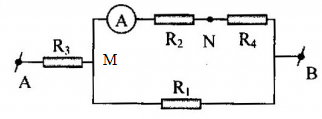
+ Ta thấy: \(\left[ {\left( {{R_2}nt{R_4}} \right)//{R_1}} \right]nt{R_3}\)
\({R_{24}} = {R_2} + {R_4} = 2 + 6 = 8\Omega \)
\(\dfrac{1}{{{R_{124}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_{24}}}} \Rightarrow {R_{124}} = \dfrac{{{R_1}{R_{24}}}}{{{R_1} + {R_{24}}}} = \dfrac{{2.8}}{{2 + 8}} = 1,6\Omega \)
\({R_{td}} = {R_{3124}} = {R_3} + {R_{124}} = 2 + 1,6 = 3,6\Omega \)
+ Cường độ dòng điện qua mạch chính: \(I = \dfrac{U}{{{R_{td}}}} = \dfrac{{7,2}}{{3,6}} = 2A\)
Ta có: \({U_{MB}} = U - {U_{AM}} = U - I.{R_3} = 7,2 - 2.2 = 3,2A\)
Lại có: \({U_{MB}} = {I_2}.{R_{24}} \Rightarrow {I_2} = \dfrac{{{U_{MB}}}}{{{R_{24}}}} = \dfrac{{3,2}}{8} = 0,4A\)
Ta có: \({U_{AN}} = {U_{AM}} + {U_{MN}} = {U_3} + {U_2} = I.{R_3} + {I_2}.{R_2} = 2.2 + 0,4.2 = 4,8V\)
Cho mạch điện kín gồm một nguồn điện có suất điện động \(10\,\,V\), điện trở trong bằng \(2\,\,\Omega \), và mạch ngoài có điện trở \(18\,\,\left( \Omega \right)\). Cường độ dòng điện chạy trong mạch là:
Cường độ dòng điện chạy trong mạch là: \(I = \dfrac{E}{{R + r}} = \dfrac{{10}}{{18 + 2}} = 0,5\,\,\left( A \right)\)
Mắc một biến trở R vào hai cực của một nguồn điện một chiều có suất điện động \(\xi = 6V\) và điện trở trong \(r\). Đồ thị biểu diễn hiệu suất H của nguồn điện theo biến trở R như hình vẽ bên. Công suất tiêu thụ cực đại trên R có giá trị bằng
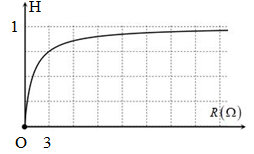
Ta có: \(H = \frac{{{U_N}}}{E} = \frac{{{R_N}}}{{{R_N} + r}}\)
Từ đồ thị ta có tại \(R = 3\Omega \) thì \(H = 0,75\)
\( \Leftrightarrow \frac{R}{{R + r}} = 0,75 \Leftrightarrow \frac{3}{{3 + r}} = 0,75 \Rightarrow r = 1\Omega \)
Công suất tiêu thụ trên R:
\({P_R} = {I^2}R = \frac{{{E^2}}}{{{{\left( {R + r} \right)}^2}}}R = \frac{{{E^2}}}{{{{\left( {\sqrt R + \frac{r}{{\sqrt R }}} \right)}^2}}}\)
\( \Rightarrow {P_{Rma{\rm{x}}}}\) khi \({\left( {\sqrt R + \frac{r}{{\sqrt R }}} \right)^2}_{\min }\)
Áp dụng BĐT Cosi ta có: \(\sqrt R + \frac{r}{{\sqrt R }} \ge 2\sqrt r = 2\)
\( \Rightarrow \sqrt R + \frac{r}{{\sqrt R }} = 2\sqrt r = 2\) khi \(\sqrt R = \frac{r}{{\sqrt R }}\)hay \(R = r\)
\( \Rightarrow {P_{R\max }} = \frac{{{E^2}}}{{4{\rm{R}}}} = \frac{{{E^2}}}{{4{\rm{r}}}} = \frac{{{6^2}}}{4} = 9W\)

