Câu hỏi:
2 năm trước
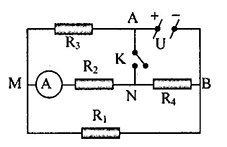
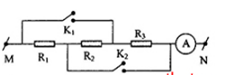
Cho mạch điện như hình vẽ: \({R_2} = 6\Omega \),\({U_{MN}} = 45V\). Biết khi \({K_1}\) đóng, \({K_2}\) mở ampe kế chỉ \(1,5A\). Khi \({K_1}\) mở, \({K_2}\) đóng thì ampe kế A chỉ \(3A\). Số chỉ của ampe kế A khi cả 2 khóa \({K_1}\) và \({K_2}\) cùng đóng là?
Trả lời bởi giáo viên
Đáp án đúng: d
Khi \({K_1}\) đóng còn \({K_2}\) mở thì mạch chỉ có \({R_3}\) \( \to {R_3} = \dfrac{{45}}{{1,5}} = 30\Omega \)
Khi \({K_2}\) đóng, \({K_1}\) mở thì mạch chỉ có \({R_1}\) \( \to {R_1} = \dfrac{{45}}{3} = 15\Omega \)
Khi \({K_1}\) và \({K_2}\) cùng đóng thì : \({R_1}//{\rm{ }}{R_2}//{\rm{ }}{R_3}\):
Điện trở tương đương của mạch:
\(\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + \dfrac{1}{{{R_3}}} = \dfrac{1}{{15}} + \dfrac{1}{6} + \dfrac{1}{{30}} = \dfrac{1}{5} \to R = 3,75\Omega \)
Ta có, số chỉ ampe kế chính là I mạch chính: \(I = \dfrac{{{U_{MN}}}}{R} = \dfrac{{45}}{{3,75}} = 12A\)
Hướng dẫn giải:
+ Áp dụng biểu thức xác định điện trở trong mạch song song: \(\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ... + \dfrac{1}{{{R_n}}}\)
+ Áp dụng biểu thức định luật Ôm cho đoạn mạch chỉ có điện trở: \(I = \dfrac{U}{R}\)
Câu hỏi khác
- Bài tập điện năng và công suất điện - định luật jun- lenxơ lý 11 có lời giải
- Bài tập định luật ôm đối với toàn mạch - mắc nguồn điện thành bộ lý 11 có lời giải
- Bài tập tính điện trở dây dẫn - biến trở có lời giải MÔN LÝ lớp 11
- Bài tập định luật ôm cho đoạn mạch chỉ có điện trở lý 11 có lời giải
- Bài tập đại cương về dòng điện không đổi - nguồn điện lý 11 có lời giải.
