Trả lời bởi giáo viên
Đáp án đúng: c
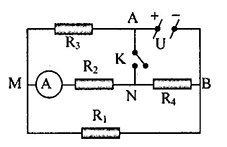
+ Ta thấy: \(\left[ {\left( {{R_2}nt{R_4}} \right)//{R_1}} \right]nt{R_3}\)
\({R_{24}} = {R_2} + {R_4} = 2 + 6 = 8\Omega \)
\(\dfrac{1}{{{R_{124}}}} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_{24}}}} \Rightarrow {R_{124}} = \dfrac{{{R_1}{R_{24}}}}{{{R_1} + {R_{24}}}} = \dfrac{{2.8}}{{2 + 8}} = 1,6\Omega \)
\({R_{td}} = {R_{3124}} = {R_3} + {R_{124}} = 2 + 1,6 = 3,6\Omega \)
+ Cường độ dòng điện qua mạch chính: \(I = \dfrac{U}{{{R_{td}}}} = \dfrac{{7,2}}{{3,6}} = 2A\)
Ta có: \({U_{MB}} = U - {U_{AM}} = U - I.{R_3} = 7,2 - 2.2 = 3,2A\)
Lại có: \({U_{MB}} = {I_2}.{R_{24}} \Rightarrow {I_2} = \dfrac{{{U_{MB}}}}{{{R_{24}}}} = \dfrac{{3,2}}{8} = 0,4A\)
Vậy số chỉ của ampe kế là \(0,4A\)
Hướng dẫn giải:
+ Áp dụng biểu thức xác định điện trở trong mạch nối tiếp: \(R{\rm{ }} = {\rm{ }}{R_1} + {\rm{ }}{R_2} + {\rm{ }}....{\rm{ }} + {\rm{ }}{R_n}\)
+ Áp dụng biểu thức xác định điện trở trong mạch song song: \(\dfrac{1}{R} = \dfrac{1}{{{R_1}}} + \dfrac{1}{{{R_2}}} + ... + \dfrac{1}{{{R_n}}}\)
+ Áp dụng biểu thức định luật Ôm cho đoạn mạch chỉ có điện trở: \(I = \dfrac{U}{R}\)
+ Áp dụng biểu thức cường độ dòng điện trong mạch nối tiếp và song song (Xem phần II + III)
Câu hỏi khác
- Bài tập điện năng và công suất điện - định luật jun- lenxơ lý 11 có lời giải
- Bài tập định luật ôm đối với toàn mạch - mắc nguồn điện thành bộ lý 11 có lời giải
- Bài tập tính điện trở dây dẫn - biến trở có lời giải MÔN LÝ lớp 11
- Bài tập định luật ôm cho đoạn mạch chỉ có điện trở lý 11 có lời giải
- Bài tập đại cương về dòng điện không đổi - nguồn điện lý 11 có lời giải.
