Đề thi thử THPT chuyên Lam Sơn - 2021
Một người cận thị phải đeo kính có độ tụ \( - 0,5dp\)sát mắt thì nhìn được vật ở vô cực mà mắt không phải điều tiết. Nếu xem tivi mà không muốn đeo kính, người đó phải ngồi cách màn hình xa nhất là
Tiêu cự của kính: \({f_k} = \frac{1}{D} = \frac{1}{{ - 0,5}} = - 2m\)
Lại có: \(O{C_V} = - {f_k} = 2m\) đây là khoảng cách lớn nhất mà người cận thị có thể quan sát được khi không đeo kính.
\( \Rightarrow \) Nếu xem tivi mà không muốn đeo kính, người đó phải ngồi cách màn hình xa nhất là 2m.
Một người cận thị có điểm cực viễn cách mắt 75 cm. Độ tụ của thấu kính cần đeo (coi kính đeo sát mắt) để người này nhìn rõ các vật ở xa vô cực mà không cần điều tiết là
Ta có: \({f_k} = - O{C_V} = - 75cm = - 0,75m\)
Độ tụ của thấu kính cần đeo: \({D_k} = \dfrac{1}{{{f_k}}} = \dfrac{1}{{ - 0,75}} = - \dfrac{4}{3}\)
Một người cận thị có điểm cực viễn cách mắt \(50\,\,cm\). Để nhìn rõ vật ở vô cực mà mắt không phải điều tiết, người này đeo sát mắt một kính có độ tụ là
Độ tụ của kính là: \({f_k} = - \dfrac{1}{{O{C_V}}} = - \dfrac{1}{{0,5}} = - 2\,\,\left( {dp} \right)\)
Một người cận thị có khoảng nhìn rõ từ 12 cm đến 44 cm. Khi đeo kính sát mắt để sửa tật thì nhìn được vật gần nhất cách mắt là
+ Người bị cận thị cần đeo TKPK để khắc phục tật này, khi kính đeo sát mắt, tiêu cự của kính cần đeo là:
\(f = - O{C_V} = - 44cm\)
+ Khi đó vật gần nhất mà người đó nhìn được cho ảnh hiện ở CC: \(d' = - 12cm\)
+ Áp dụng công thức thấu kính ta có:
\(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f} \Rightarrow d = \frac{{d'f}}{{d' - f}} = \frac{{ - 12.( - 44)}}{{ - 12 - ( - 44)}} = 16,{5_{}}cm\)
Một người mắt tốt có khoảng nhìn rõ ngắn nhất là 25 cm. Độ biến thiên độ tụ của mắt người đó khi quan sát các vật là
Ta có:
+ Khi quan sát vật ở vô cực: \(d = \infty \) khi đó \({D_1} = \dfrac{1}{{OV}}\)
+ Khi quan sát vật ở cực cận: \(d = O{C_C}\) khi đó \({D_2} = \dfrac{1}{{O{C_C}}} + \dfrac{1}{{OV}}\)
+ Độ biến thiên độ tụ của mắt người khi quan sát các vật: \(\Delta D = {D_2} - {D_1} = \dfrac{1}{{O{C_C}}} = \dfrac{1}{{0,25}} = 4\)
Một người mắt cận có điểm cực viễn cách mắt 50cm. Để nhìn rõ vật ở xa vô cùng mà mắt không phải điều tiết, người đó cần đeo sát mắt một kính có độ tụ bằng:
Ta có: \(O{C_v} = 50cm = 0,5m\)
Tiêu cự của kính: \({f_k} = - O{C_v} = - 0,5m\)
Độ tụ của kính: \({D_k} = \dfrac{1}{{{f_k}}} = \dfrac{1}{{ - 0,5}} = - 2dp\)
Một người cận thị có điểm cực viễn cách mắt 50 cm. Tính độ tụ của kính phải đeo sát mắt để có thể nhìn vật ở vô cực mà không cần phải điều tiết:
Mắt nhìn thấy vật ở vô cực mà không cần phải điều tiết khi ảnh của vật nằm ở điểm cực viễn của mắt.
\(\begin{gathered}
\to \left\{ {\begin{array}{*{20}{l}}
{{\text{d = }}\infty } \\
{{\text{d' = - 50}}\,\,{\text{cm = - 0}},{\text{5}}\,\,{\text{m}}}
\end{array}} \right. \hfill \\
\Rightarrow {\text{D = }}\frac{{\text{1}}}{{\text{d}}}{\text{ + }}\frac{{\text{1}}}{{{\text{d'}}}}{\text{ = }}\frac{{\text{1}}}{\infty }{\text{ + }}\frac{{\text{1}}}{{{\text{ - 0}},{\text{5}}}}{\text{ = - 2}}\,\,{\text{dp}} \hfill \\
\end{gathered} \)
Một người cận thị lớn tuổi chỉ còn nhìn thấy rõ các vật trong khoảng cách mắt \(50cm \div 70cm\). Tính độ tụ của kính cần đeo để người này có thể đọc được sách gần mắt nhất cách mắt 25cm
Để đọc sách đặt gần mắt nhất, cách mắt 25cm, phải đeo kính có tiêu cự f xác định bởi:
\(\dfrac{1}{{25}} - \dfrac{1}{{50}} = \dfrac{1}{f} \Rightarrow f = 50cm = 0,5m\)
Độ tụ của kính: \(D = \dfrac{1}{f} = \dfrac{1}{{0,5}} = 2dp\)
Một người cận thị lớn tuổi chỉ còn nhìn thấy rõ các vật trong khoảng cách mắt \(45cm \div \dfrac{{200}}{3}cm\). Tính độ tụ của kính cần đeo để người này có thể nhìn xa vô cùng không điều tiết.
Ta có hình vẽ:
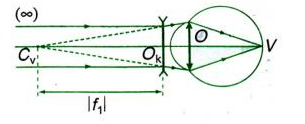
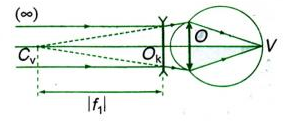
Ta có: \({f_1} = - {O_k}{C_v} = - \dfrac{{200}}{3}cm = - \dfrac{2}{3}m\)
Độ tụ của kính: \(D = \dfrac{1}{{{f_1}}} = \dfrac{1}{{ - \dfrac{2}{3}}} = - 1,5dp\)
Vật AB ở vô cực?
Ta có, mắt bình thường cho ảnh trên võng mạc nên \( \to d' = OV = 15mm\)
+ Khi nhìn vật ở vô cực \(\left( {d = \infty } \right)\), ảnh hiện trên võng mạc.
+ Tiêu cự của thủy tinh thế là:
\(\begin{array}{l}\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} = \frac{1}{{OV}}\\ \to f = OV = 15mm\end{array}\)
+ Độ tụ của thủy tinh thể: \(D = \frac{1}{f} = \frac{1}{{{{15.10}^{ - 3}}}} = 66,67{\rm{d}}p\)
Mắt người này bị tật gì?
Ta thấy, mắt người này nhìn xa nhất là 50cm nên mắt người này bị cận thị
Số kính của \({L_1};{L_2}\)là:
- Khi đeo kính \({L_1}\):
+ Qua \({L_1}\) vật ở vô cực cho ảnh ảo ở điểm cực viễn của mắt cận.
Ta có: \(\left\{ \begin{array}{l}d = \infty \\d' = - 50cm\end{array} \right. \to \frac{1}{{{f_1}}} = \frac{1}{\infty } + \frac{1}{{ - 50}} \to {f_1} = - 50cm = - 0,5m\)
+ Độ tụ: \({D_1} = \frac{1}{{{f_1}}} = - 2{\rm{d}}p\)
- Khi đeo kính \({L_2}\) :
+ Vật ở cách mắt 25cm cho ảnh ảo ở điểm cực cận của mắt.
Ta có: \(\left\{ \begin{array}{l}d = 25cm\\d' = - 20cm\end{array} \right. \to \frac{1}{{{f_2}}} = \frac{1}{{25}} + \frac{1}{{ - 20}} \to {f_2} = - 100cm = - 1m\)
+ Độ tụ: \(D = \frac{1}{f} = - 1{\rm{d}}p\)
Tiêu cự của thấu kính là:
+ Vì vật thật cho ảnh thật nên \(k < 0 \leftrightarrow - \frac{1}{2} = - \frac{{d'}}{d} \to d' = \frac{d}{2} = 7,5cm\)
+ Tiêu cự của thấu kính \(\left( {{L_1}} \right)\): \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} \to f = \frac{{{\rm{dd}}'}}{{d + d'}} = \frac{{15.7,5}}{{15 + 7,5}} = 5cm\)
Vật AB cách mắt 80cm?
Ta có, mắt bình thường cho ảnh trên võng mạc nên \( \to d' = OV = 15mm\)
+ \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} = \frac{1}{{80}} + \frac{1}{{1,5}} = 1,47cm\)
+ Độ tụ của thủy tinh thể: \(D = \frac{1}{f} = \frac{1}{{0,0147}} = 67,92{\rm{d}}p\)
Vật AB ở vô cực?
Ta có, mắt bình thường cho ảnh trên võng mạc nên \( \to d' = OV = 15mm\)
+ Khi nhìn vật ở vô cực \(\left( {d = \infty } \right)\), ảnh hiện trên võng mạc.
+ Tiêu cự của thủy tinh thế là:
\(\begin{array}{l}\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} = \frac{1}{{OV}}\\ \to f = OV = 15mm\end{array}\)
+ Độ tụ của thủy tinh thể: \(D = \frac{1}{f} = \frac{1}{{{{15.10}^{ - 3}}}} = 66,67{\rm{d}}p\)
Vật AB ở vô cực?
Ta có, mắt bình thường cho ảnh trên võng mạc nên \( \to d' = OV = 15mm\)
+ Khi nhìn vật ở vô cực \(\left( {d = \infty } \right)\), ảnh hiện trên võng mạc.
+ Tiêu cự của thủy tinh thế là:
\(\begin{array}{l}\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} = \frac{1}{{OV}}\\ \to f = OV = 15mm\end{array}\)
+ Độ tụ của thủy tinh thể: \(D = \frac{1}{f} = \frac{1}{{{{15.10}^{ - 3}}}} = 66,67{\rm{d}}p\)
Điểm \({C_C}\) cách mắt \(10cm\), khi đeo kính trên (sát mắt) thì người đó nhìn thấy điểm gần nhất cách mắt bao nhiêu?
Khi đeo kính trên mà nhìn vật cách mắt đoạn gần nhất là d thì ảnh ảo sẽ hiện ở điểm cực cận của mắt \(\left( {d' = - 10cm} \right)\)
Ta có:
\(\begin{array}{l}D = \frac{1}{d} + \frac{1}{{d'}} \leftrightarrow - 2 = \frac{1}{d} + \frac{1}{{ - 0,1}}\\ \to d = 0,125m = 12,5cm\end{array}\)
Muốn nhìn thấy vật ở vô cực không phải điều tiết, người đó phải đeo kính có độ tụ bao nhiêu (coi kính đeo sát mắt)?
+ Khi mắt nhìn ở vô cực thì không phải điều tiết.
=> Người này phải đeo kính có độ tụ \({D_1}\) sao cho vật đặt ở vô cực cho ảnh ảo ở điểm cực viễn của mắt.
Do đó, ta có: \(D = \frac{1}{\infty } + \frac{1}{{ - O{C_V}}} = - \frac{1}{{0,5}} \to D = - 2{\rm{d}}p\)
Mắt người này bị tật gì?
Ta thấy, mắt người này nhìn xa nhất là 50cm nên mắt người này bị cận thị
Mắt người này bị tật gì?
Ta thấy, mắt người này nhìn xa nhất là 50cm nên mắt người này bị cận thị
