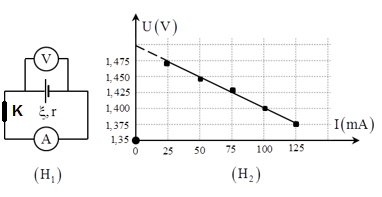
Để đo suất điện động và điện trở trong của một pin, một nhóm học sinh đã mắc sơ đồ mạch điện như hình vẽ (Hình 1). Vôn kế có điện trở rất lớn, đóng công tắc K và điều chỉnh biến trở, số chỉ của vôn kế và ampe kế ứng với mỗi lần đo được cho trên hình vẽ bên (Hình 2). Nhóm học sinh này tính được giá trị trung bình của suất điện động và điện trở trong của pin đó lần lượt là
Cường độ dòng điện qua mạch = Số chỉ ampe kế : \(I=\frac{E}{r+R}\)
Số chỉ vôn kế = điện áp hai đầu điện trở : \(U=\text{IR=}\frac{\text{ER}}{R+r}\)
Từ đồ thị ta thấy khi I = 0 thì UV = E = 1,5V
Khi I = 125mA = 0,125A thì U = 1,375V => R = 11Ω
Ta có: \(U=\text{IR=}\frac{\text{ER}}{R+r}\Rightarrow 1,375=\frac{1,5.11}{11+r}\Rightarrow r=1\Omega \)
Phát biểu nào sau đây là không đúng?
A, B, C – đúng
D – sai vì: Chiều qui ước của dòng điện là chiều dịch chuyển có hướng của các điện tích dương (ngược chiều dịch chuyển của electron).
Phát biểu nào sau đây là không đúng?
A, B, D – đúng
C – sai vì : Dòng điện có tác dụng hóa học là đúng nhưng ví dụ về tác dụng hóa học là acquy nóng lên khi nạp điện là sai
Ví dụ về tác dụng hóa học của dòng điện : mạ đồng, mạ vàng, …
Điện tích của electron là \( - {\rm{ }}{1,6.10^{ - 19}}\left( C \right)\), điện lượng chuyển qua tiết diện thẳng của dây dẫn trong \(30{\rm{ }}\left( s \right)\) là \(15{\rm{ }}\left( C \right)\) . Số êlectron chuyển qua tiết diện thẳng của dây dẫn trong thời gian một giây là :
+ Cường độ dòng điện trong mạch : \(I = \frac{q}{{{t_1}}} = \frac{{15}}{{30}} = 0,5A\)
+ Số electron chuyển chuyển qua tiết diện thẳng của dây dẫn trong thời gian một giây là :
\(n = \frac{{I.t}}{{\left| e \right|}} = \frac{{0,5.1}}{{\left| { - {{1,6.10}^{ - 19}}} \right|}} = {3,125.10^{18}}\)
Đồ thị mô tả định luật Ôm là:
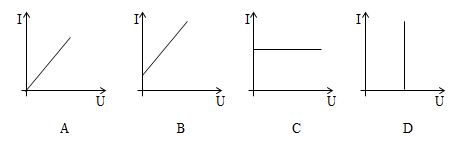
Biểu thức định luật Ôm: \(I = \frac{U}{R}\) đường đặc trưng Vôn – Ampe là một đường thẳng đi qua gốc toạ độ.
Suất điện động của nguồn điện đặc trưng cho :
Suất điện động là đại lượng đặc trưng cho khả năng thực hiện công của nguồn điện.
Đoạn mạch gồm điện trở \({R_1} = 100\Omega \) mắc nối tiếp với điện trở \({R_2} = 300\Omega \), điện trở toàn mạch là:
\(\left( {{R_1}{\rm{ }}nt{\rm{ }}{R_2}} \right)\)
=> Điện trở toàn mạch là: \({R_b} = {R_1} + {R_2} = 100 + 300 = 400\Omega \)
Cho đoạn mạch gồm điện trở \({R_1} = 100\Omega \), mắc nối tiếp với điện trở \({R_2} = 200\Omega \) , hiệu điên thế giữa hai đầu đoạn mạch là \(12{\rm{ }}\left( V \right)\). Hiệu điện thế giữa hai đầu điện trở \({R_1}\) là:
\(\left( {{R_1}{\rm{ }}nt{\rm{ }}{R_2}} \right)\)
=> Điện trở toàn mạch là: \({R_b} = {R_1} + {R_2} = 100 + 200 = 300\Omega \)
+ Cường độ dòng điện trong mạch: \(I = \frac{U}{{{R_b}}} = \frac{{12}}{{300}} = 0,04A\)
+ Hiệu điện thế trên \({R_1}\) là \({U_1} = {I_1}.{R_1} = 0,04.100 = 4V\)
Đoạn mạch gồm điện trở ba điện trở \({R_1} = 25\Omega \) và \({R_2} = {R_3} = 50\Omega \) mắc song song với nhau, điện trở toàn mạch là:
Ta có: \({R_1}//{R_2}//{R_3}\)
=> Điện trở tương đương của mạch:
\(\begin{array}{l}\frac{1}{{{R_b}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + \frac{1}{{{R_3}}} = \frac{1}{{25}} + \frac{1}{{50}} + \frac{1}{{50}} = \frac{2}{{25}}\\ \to {R_b} = 12,5\Omega \end{array}\)
Cho đoạn mạch gồm điện trở \({R_1} = 100\Omega \), mắc nối tiếp với điện trở \({R_2} = 200\Omega \). Đặt vào hai đầu đoạn mạch một hiệu điện thế \(U\) khi đó hiệu điên thế giữa hai đầu điện trở \({R_1}\) là \(6{\rm{ }}\left( V \right)\). Hiệu điện thế giữa hai đầu đoạn mạch là:
+ Điện trở tương đương của mạch: \({R_b} = {R_1} + {R_2} = 100 + 200 = 300\Omega \)
+ Hiệu điện thế trên \({U_1} = 6V\)
Cường độ dòng điện \(I = {I_1} = \dfrac{{{U_1}}}{{{R_1}}} = \dfrac{6}{{100}} = 0,06A\)
+ Hiệu điện thế giữa hai đầu đoạn mạch: \(U = I.{R_b} = 0,06.300 = 18V\)
Công của nguồn điện được xác định theo công thức:
Công của nguồn điện được xác định bởi biểu thức: \(A = qE = EIt\)
Công của dòng điện có đơn vị là:
Công của dòng điện: \(A = qU = UIt\) có đơn vị là \(kWh\)
Hai bóng đèn ${Đ_1}\left( {220V-25W} \right)$ , ${Đ_2}\left( {220V-100W} \right)$ khi sáng bình thường thì:
+ Hai bóng đèn ${Đ_1}\left( {220V-25W} \right)$, ${Đ_2}\left( {220V-100W} \right)$ khi sáng bình thường thì hiệu điện thế đặt vào hai đầu bóng đèn là $U{\rm{ }} = {\rm{ }}220{\rm{ }}\left( V \right)$
+ Công suất của mỗi bóng đèn lần lượt là ${P_1} = {\rm{ }}25{\rm{ }}\left( W \right)$ và ${P_2} = {\rm{ }}100{\rm{ }}\left( W \right){\rm{ }} = {\rm{ }}4{P_1}$
+ Cường độ dòng điện qua bóng đèn được tính theo công thức $I = \dfrac{P}{U}$ suy ra cường độ dòng điện qua bóng đèn ${Đ_2}$ lớn gấp bốn lần cường độ dòng điện qua bóng đèn ${Đ_1}$.
Hai bóng đèn có công suất định mức bằng nhau, hiệu điện thế định mức của chúng lần lượt là \({U_1} = 110\left( V \right)\) và \({U_2} = 220\left( V \right)\). Tỉ số điện trở của chúng là:
Ta có: \(P = UI = \dfrac{{{U^2}}}{R}\)
Theo đề bài ta có: \({P_1} = {P_2}\)
Ta suy ra: \(\dfrac{{U_1^2}}{{{R_1}}} = \dfrac{{U_2^2}}{{{R_2}}} \to \dfrac{{{R_1}}}{{{R_2}}} = \dfrac{{U_1^2}}{{U_2^2}} = \dfrac{{{{110}^2}}}{{{{220}^2}}} = \dfrac{1}{4}\)
Để bóng đèn loại \(120V - 60W\)sáng bình thường ở mạng điện có hiệu điện thế là $220V$, người ta phải mắc nối tiếp với bóng đèn một điện trở có giá trị:
Ta có:
- Bóng đèn loại \(120V - 60W\) sáng bình thường thì hiệu điện thế giữa hai đầu bóng đèn là \(120V\), cường độ dòng điện qua bóng đèn là \(I = \dfrac{P}{U} = \dfrac{{60}}{{120}} = 0,5A\)
- Để bóng đèn sáng bình thường ở mạng điện có hiệu điện thế là \(220V\), người ta phải mắc nối tiếp với bóng đèn một điện trở sao cho hiệu điện thế giữa hai đầu điện trở là \({U_R} = 220 - 120 = 100V\)
=> Điện trở cần mắc nối tiếp có giá trị là: \(R = \dfrac{{{U_R}}}{I} = \dfrac{{100}}{{0,5}} = 200\Omega \)
Biểu thức định luật Ôm cho toàn mạch trong trường hợp mạch ngoài chứa máy thu là:
Biểu thức định luật Ôm cho toàn mạch trong trường hợp mạch ngoài có máy thu là: \(I = \frac{{E - {E_p}}}{{R + r + r'}}\)
Một nguồn điện có điện trở trong \(0,1\Omega \) được mắc với điện trở \(4,8\Omega \) thành mạch kín. Khi đó hiệu điện thế giữa hai cực của nguồn điện là \(12V\). Suất điện động của nguồn điện là:
- Cường độ dòng điện trong mạch là \(I = \dfrac{U}{R} = \dfrac{{12}}{{4,8}} = 2,5(A)\)
- Suất điện động của nguồn điện là: \(E = I\left( {R + r} \right) = {\rm{IR}} + {\rm{Ir}} = U + {\rm{Ir}} = 12 + 2,5.0,1 = 12,25V\)
Người ta mắc hai cực của nguồn điện với một biến trở có thể thay đổi từ \(0\) đến vô cực. Khi giá trị của biến trở rất lớn thì hiệu điện thế giữa hai cực của nguồn điện là \(4,5\left( V \right)\). Giảm giá trị của biến trở đến khi cường độ dòng điện trong mạch là \(2A\) thì hiệu điện thế giữa hai cực của nguồn điện là \(4\left( V \right)\). Suất điện động và điện trở trong của nguồn điện là:
- Khi giá trị của biến trở rất lớn thì hiệu điện thế giữa hai cực của nguồn điện là \(4,5V\)
Suy ra suất điện động của nguồn điện là \(E = 4,5V\)
- Áp dụng công thức: \(E = U + Ir\) với \(I = 2A\) và \(U = 4V\)
Ta tính được điện trở trong của nguồn điện là: \(r = 0,25\Omega \)
Một nguồn điện có suất điện động \(E = 6\left( V \right)\), điện trở trong \(r = 2\left( \Omega \right)\), mạch ngoài có điện trở \(R\). Để công suất tiêu thụ ở mạch ngoài là \(4W\) thì điện trở \(R\) phải có giá trị:
+ Công suất tiêu thụ mạch ngoài là: $P = {I^2}R$, cường độ dòng điện trong mạch là $I = \dfrac{E}{{R + r}}$
Suy ra: $P = {I^2}R = \dfrac{{{E^2}}}{{{{\left( {R + r} \right)}^2}}}R$
+ Với $E = 6V;r = 2\Omega ;P = 4W$ ta được:
\(\begin{array}{l}4 = \dfrac{{{6^2}}}{{{{\left( {R + 2} \right)}^2}}}R\\ \leftrightarrow 4{R^2} + 16R + 16 = 36R\\ \to \left[ \begin{array}{l}R = 4\Omega \\R = 1\Omega \end{array} \right.\end{array}\)
Dùng một nguồn điện để thắp sáng lần lượt hai bóng đèn có điện trở \({R_1} = 2\Omega \) và \(R_2 = 8\Omega \), khi đó công suất tiêu thụ của hai bóng đèn là như nhau. Điện trở trong của nguồn điện là:
Công suất tiêu thụ mạch ngoài là: \(P = {I^2}R\), cường độ dòng điện trong mạch là \(I = \dfrac{E}{{R + r}}\)
Suy ra: \(P = {I^2}R = \dfrac{{{E^2}}}{{{{\left( {R + r} \right)}^2}}}R\)
+ Khi \(R = {R_1}\) ta có \({P_1} = {\left( {\dfrac{E}{{{R_1} + r}}} \right)^2}{R_1}\)
+ Khi \(R = {R_2}\) ta có \({P_2} = {\left( {\dfrac{E}{{{R_2} + r}}} \right)^2}{R_2}\)
Theo bài ra:
$\begin{array}{l}{P_1} = {P_2} \leftrightarrow \dfrac{{{E^2}}}{{{{\left( {{R_1} + r} \right)}^2}}}{R_1} = \dfrac{{{E^2}}}{{{{\left( {{R_2} + r} \right)}^2}}}{R_2}\\ \leftrightarrow {\left( {{R_2} + r} \right)^2}{R_1} = {\left( {{R_1} + r} \right)^2}{R_2}\\ \leftrightarrow {\left( {8 + r} \right)^2}.2 = {\left( {2 + r} \right)^2}.8\\ \leftrightarrow r = 4\Omega \end{array}$

