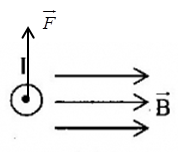
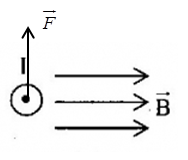
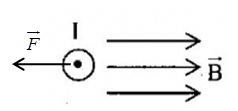Một đoạn dây dẫn\(\;CD\) chiều dài \({\rm{l}}\) mang dòng điện \(I\) chạy qua đặt trong từ trường sao cho \(\;CD\) song song với các đường sức từ. Độ lớn lực từ tác dụng lên dây \(\;CD\) là
Độ lớn lực từ tác dụng lên đoạn dây dẫn mang dòng điện đặt trong từ trường là:
\(F = BI{\rm{l}}\sin \alpha = BI{\rm{l}}\sin {0^0} = 0\)
Một đoạn dây dẫn dài \({\rm{l}} = 0,5\,\,m\) đặt trong từ trường đều sao cho dây dẫn hợp với vectơ cảm ứng từ \(\overrightarrow B \) một góc \(\alpha = {45^0}\). Biết cảm ứng từ \(B = {2.10^{ - 3}}\,\,T\) và dây dẫn chịu lực từ \(F = {4.10^{ - 2}}\,\,N\). Cường độ dòng điện trong dây dẫn là
Lực từ tác dụng lên đoạn dây dẫn là:
\(F = IB{\rm{l}}\sin \alpha \Rightarrow I = \dfrac{F}{{B{\rm{l}}\sin \alpha }} = \dfrac{{{{4.10}^{ - 2}}}}{{{{2.10}^{ - 3}}.0,5.\sin {{45}^0}}} = 40\sqrt 2 \,\,\left( A \right)\)
Một đoạn dây dẫn dài \(10\,\,cm\) đặt trong từ trường đều và hợp với vectơ cảm ứng từ một góc \({30^0}\). Dòng điện chạy qua dây có cường độ \(0,75\,\,A\). Lực từ tác dụng lên đoạn dây đó là \(4,{5.10^{ - 2}}\,\,N\). Cảm ứng từ của từ trường đó có độ lớn là
Lực từ tác dụng lên đoạn dây dẫn là:
\(F = IB{\rm{l}}\sin \alpha \Rightarrow B = \dfrac{F}{{I{\rm{l}}\sin \alpha }} = \dfrac{{4,{{5.10}^{ - 2}}}}{{0,75.0,1.\sin {{30}^0}}} = 1,2\,\,\left( T \right)\)
Công thức tính lực từ tác dụng lên một đoạn dây dẫn chiều dài mang dòng điện đặt trong từ trường đều là:
Công thức tính lực từ tác dụng lên một đoạn dây dẫn chiều dài \({\rm{l}}\) mang dòng điện đặt trong từ trường đều là:
\(F = BI{\rm{l}}sin\alpha \)
Lực từ tác dụng lên một đoạn dây dẫn mang dòng điện được xác định bởi biểu thức:
Lực từ tác dụng lên một đoạn dây dẫn mang dòng điện được xác định bởi biểu thức: \(F = BIl\sin \alpha \)
Một đoạn dây dẫn dài \(1,5\,\,m\) mang dòng điện \(10\,\,A\), đặt vuông góc trong một từ trường đều có độ lớn cảm ứng từ \(1,2\,\,T\). Nó chịu một lực từ tác dụng là
Lực từ tác dụng lên đoạn dây dẫn là:
\(F = IB{\rm{l}}\sin \alpha = 10.1,2.1,5.\sin {90^0} = 18\,\,\left( N \right)\)
Treo đoạn dây dẫn MN có chiều dài \(L = 25cm\), khối lượng một đơn vị chiều dài \(0,04kg/m\) bằng hai dây mảnh nhẹ sao cho dây dẫn nằm ngang. Biết cảm ứng từ có chiều như hình vẽ, độ lớn cảm ứng từ \(B = 0,04T\). Lấy \(g = 10m/{s^2}\). Cho \(I = 16A\) có chiều từ M đến N, xác định lực căng của mỗi dây?
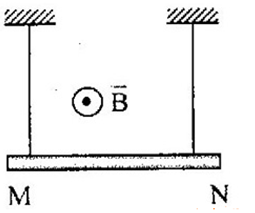
- Bước 1:
Ta có các lực tác dụng lên đoạn dây gồm: Trọng lực \(\overrightarrow P \), lực căng dây \(\overrightarrow {{T_1}} ,\overrightarrow {{T_2}} \), và lực từ \(\overrightarrow F \)
- Bước 2:
+ Áp dụng quy tắc bàn tay trái, ta có chiều của lực từ như hình vẽ
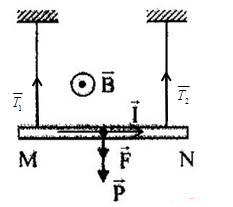
- Bước 3:
Ta có: khối lượng của đoạn dây: \(m = 0,04.L = 0,04.0,25 = 0,01kg\)
Dây dẫn cân bằng, áp dụng định luật II – Niuton, ta có:
\(\overrightarrow F + \overrightarrow P + \overrightarrow {{T_1}} + \overrightarrow {{T_2}} = \overrightarrow 0 \) (1)
Chọn chiều dương hướng lên,
Chiếu (1), ta được:
\(\begin{array}{l} - F - P + {T_1} + {T_2} = 0\\ \Rightarrow {T_1} + {T_2} = F + P\end{array}\)
Lại có: \({T_1} = {T_2}\)
\(\begin{array}{l} \Rightarrow 2{T_1} = F + P = BIL\sin {90^0} + mg\\ \Rightarrow {T_1} = \dfrac{{0,04.16.0,25.1 + 0,01.10}}{2} = 0,13N\end{array}\)
\( \Rightarrow {T_1} = {T_2} = 0,13N\)
Hai thanh ray nằm ngang song song cách nhau \(0,2cm\). Một thanh kim loại đặt lên hay thanh ray. Cho dòng điện \(10A\) chạy qua thanh kim loại đặt lên hay thanh ray. Biết hệ số ma sát giữa thanh kim loại và thanh ray là \(\mu = 0,01\)và khối lượng thanh kim loại là \(0,5kg\). Cảm ứng từ B có giá trị như thế nào để thanh kim loại có thể chuyển động?
Ta có:
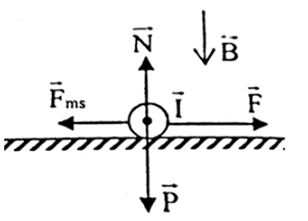
Để thanh kim loại chuyển động thì lực từ phải thắng lực masát hay lực từ lớn hơn lực masát
\(\begin{array}{l} \to F > {F_{m{\rm{s}}}} \leftrightarrow BIl\sin {90^0} > \mu mg\\ \to B > \dfrac{{\mu mg}}{{Il}} = \dfrac{{0,01.0,5.10}}{{10.0,{{2.10}^{ - 2}}}} = 2,5T\end{array}\)
Hai thanh ray nằm ngang song song và cách nhau \(l = 25cm\) đặt trong từ trường đều \(\overrightarrow B \) thẳng đứng, \(B = 0,02T\). Một thanh kim loại đặt trên ray vuông góc với ray. Nối ray với nguồn điện \(E = 11V,r = 0,5\Omega \), điện trở của thanh kim loại và dây nối \(R = 5\Omega \). Lực từ tác dụng lên thanh kim loại có giá trị:
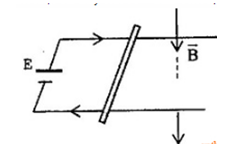
+ Theo định luật Ôm, ta có: \(I = \dfrac{E}{{R + r}} = \dfrac{{11}}{{5 + 0,5}} = 2A\)
+ Lực từ tác dụng lên thanh kim loại: \(F = BIl{\rm{sin}}{90^0} = 0,02.2.0,25.{\rm{sin}}{90^0} = 0,01N\)
Một thanh kim loại CD có chiều dài \(l{\rm{ }} = {\rm{ }}20cm\) khối lượng \(m{\rm{ }} = {\rm{ }}100g\) đặt vuông góc với 2 thanh ray song song nằm ngang và nối với nguồn điện như hình vẽ. Hệ thống đặt trong từ trường đều có \(B{\rm{ }} = {\rm{ }}0,2T\) phương chiều như vẽ, dòng điện I= 10A có chiều từ D đến C. Biết hệ số ma sát giữa CD và thanh ray là \(\mu = 0,1\). Bỏ qua điện trở của các thanh ray, điện trở tại nơi tiếp xúc và dòng điện cảm ứng trong mạch. Nâng hai đầu thanh AB của ray lên để hợp với mặt phẳng ngang góc \({30^0}\). Xác định gia tốc chuyển động của thanh bắt đầu trượt với vận tốc ban đầu bằng \(0\).
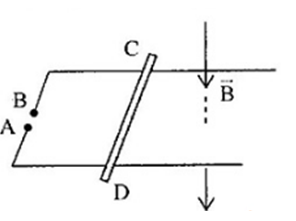
Ta có, các lực tác dụng lên thanh gồm: trọng lực \(\overrightarrow P \) , lực ma sát \(\overrightarrow {{F_{ms}}} \), phản lực \(\overrightarrow N \) và lực từ \(\overrightarrow F \) có hướng như hình vẽ:
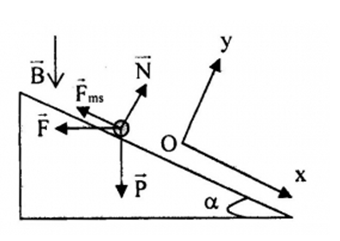
Chọn hệ trục Oxy như hình vẽ
+ Áp dụng định luật II – Niuton, ta có: \(\overrightarrow N + \overrightarrow P + \overrightarrow {{F_{ms}}} + \overrightarrow F = m\overrightarrow a \) (*)
Chiếu (*) lên các phương ta được:
\(\left\{ \begin{array}{l}Ox:P\sin \alpha - F\cos \alpha - {F_{ms}} = ma{\rm{ }}\left( 1 \right)\\Oy:N - Pcos\alpha - F\sin \alpha = 0{\rm{ }}\left( 2 \right)\end{array} \right.\)
Từ (2) ta suy ra: \(N = Pcos\alpha + F\sin \alpha \)
+ Lực ma sát: \({F_{ms}} = \mu N = \mu \left( {Pcos\alpha + F\sin \alpha } \right)\)
Lực từ: \(F = BIl\sin {90^0} = BIl\)
=> Lực ma sát: \({F_{ms}} = \mu \left( {Pcos\alpha + BIl\sin \alpha } \right)\)
Thay vào (1) ta được:
\(\begin{array}{l}P\sin \alpha - BIlcos\alpha - \mu \left( {Pcos\alpha + BIl\sin \alpha } \right) = ma\\ \Rightarrow a = \dfrac{{P\left( {\sin \alpha - \mu cos\alpha } \right) - BIl\left( {cos\alpha + \mu \sin \alpha } \right)}}{m}\\ = \dfrac{{0,1.10\left( {\sin {{30}^0} - 0,1.cos{{30}^0}} \right) - 0,2.10.0,2\left( {cos{{30}^0} + 0,1.\sin {{30}^0}} \right)}}{{0,1}}\\ \approx 0,47m/{s^2}\end{array}\)
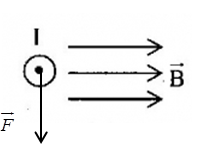
Một đoạn dây dẫn mang dòng điện đặt trong từ trường đều có các đường sức từ thẳng đứng hướng từ trên xuống như hình vẽ. Lực từ tác dụng lên đoạn dây có chiều
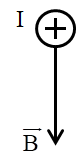
Áp dụng quy tắc bàn tay trái, lực từ tác dụng lên đoạn dây có chiều nằm ngang hướng từ phải sang trái.
Một đoạn dây dẫn dài 1,5m mang dòng điện 10A, đặt vuông góc trong một từ trường đều có độ lớn cảm ứng từ 1,2T. Nó chịu một lực từ tác dụng là bao nhiêu?
Lực từ tác dụng lên đoạn dây dẫn là: \(F = BIl\sin \alpha = 1,2.10.1,5.\sin {90^0} = 18\,\,\left( N \right)\)
Một đoạn dây dẫn đặt trong một từ trường đều có cảm ứng từ 0,35T. Khi dòng điện cường độ 14,5A chạy qua đoạn dây dẫn, thì đoạn dây dẫn này bị tác dụng một lực từ bằng 1,65N. Nếu hướng của dòng điện hợp với hướng của từ trường một góc 300 thì độ dài của đoạn dây dẫn bằng bao nhiêu ?
Ta có: \(\left\{ \begin{array}{l}B = 0,35T\\I = 14,5A\\F = 1,65N\\\alpha = \left( {\overrightarrow B ;\overrightarrow l } \right) = {30^0}\end{array} \right.\)
Lực từ tác dụng lên dây dẫn: \(F = B.I.l.\sin \alpha \Rightarrow l = \dfrac{F}{{BI.\sin \alpha }} = \dfrac{{1,65}}{{0,35.14,5.\sin 30}} \approx 0,65m\)
Một đoạn dây dẫn đồng chất có khối lượng m = 30g, chiều dài l= 50cm. Đầu trên của dây được treo vào điểm O và có thể quay tự do quanh O. Đầu dưới của đoạn dây chạm vào thủy ngân đựng trong một chiếc chậu. Đặt toàn bộ đoạn dây trong từ trường đều có phương nằm ngang, B = 0,03T. Lấy g =10m/s2. Khi cho dòng điện I =10A chạy qua đoạn dây thì đoạn dây lệch ra khỏi phương thẳng đứng một góc α bằng bao nhiêu?
Áp dụng công thức tính lực từ:
\(F = B.I.l.\sin \alpha = 0,03.10.0,5.\sin {90^0} = 0,15N\)
Trọng lực tác dụng lên dây là: P =m.g = 0,03.10=0,3N
Khi đó sợi dây chịu tác dụng của hai lực F và P, nó ở trạng thái cân bằng như hình vẽ
Áp dụng công thức lượng giác ta có:
\(\tan \alpha = \frac{F}{P} = \frac{{0,15}}{{0,3}} = \frac{1}{2} = > \alpha \approx {30^0}\)
Đề thi THPT QG - 2020
Một đoạn dây dẫn thẳng có chiều dài \(l\) được đặt trong từ trường đều có cảm ứng từ \(\overrightarrow B \) hợp với đoạn dây một góc \(\alpha \). Khi cho dòng điện có cường độ \(I\) chạy trong đoạn dây thì độ lớn lực từ tác dụng lên đoạn dây là
Lực từ tác dụng lên đoạn dây: \(F = BIl\sin \alpha \).
Phát biểu nào sau đây là đúng?
Lực từ tác dụng lên một đoạn dây dẫn mang dòng điện đặt trong từ trường đều
Lực từ tác dụng lên đoạn dây dẫn mang dòng điện: \(F = BIl{\rm{sin}}\alpha\) với \( {\rm{ }}\alpha {\rm{ = }}\widehat {\vec B,l}\)
A – sai vì: Lực từ tỉ lệ thuận với cường độ dòng điên
B – sai vì: Lực tử tỉ lệ thuận với chiều dài của đoạn dây
C – sai vì: \(F\sim \sin \alpha \) chứ không phải \(\alpha \)
D - đúng
Phát biểu nào sau đây là không đúng?
Quy tắc bàn tay trái: Đặt bàn tay trái sao cho các đường sức từ đâm xuyên vào lòng bàn tay, dòng điện chạy từ cổ tay đến ngón tay, thì ngón cái choãi ra là chiều của lực từ tác dụng lên dòng điện
=> Chiều của lực từ tác dụng lên dòng điện phụ thuộc vào chiều dòng điện và chiều cảm ứng từ
=> Khi thay đổi chiều của dòng điện hoặc cảm ứng từ thì chiều của lực từ sẽ thay đổi
Chiều của lực từ không phụ thuộc vào độ lớn của cường độ dòng điện
=> Phương án C - sai
Phát biểu nào sau đây là không đúng?
Ta có:
Lực từ có phương vuông góc với mặt phẳng \(\left( {\overrightarrow B ,l} \right)\)
=> Lực từ có phương vuông góc với đường cảm ứng từ và có phương vuông góc với dòng điện
=> Phương án D - sai
Một dây dẫn có dòng điện \(I\) nằm ngang đặt trong từ trường có các đường sức từ thẳng đứng từ trên xuống như hình vẽ.
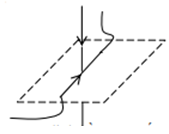
Lực từ tác dụng lên đoạn dây dẫn có chiều:
Đặt bàn tay trái sao cho các đường sức từ đâm xuyên vào lòng bàn tay, dòng điện chạy từ cổ tay đến ngón tay, thì ngón cái choãi ra là chiều của lực từ tác dụng lên dòng điện
=> Lực từ trong trường hợp trên: có phương ngang, hướng sang trái
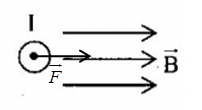
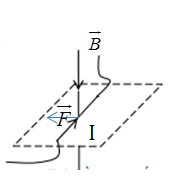
Một dây dẫn thẳng có dòng điện I đặt trong vùng không gian có từ trường đều như hình vẽ.
Xác định véctơ của đại lượng còn thiếu:
Quy tắc bàn tay trái: Đặt bàn tay trái sao cho các đường sức từ đâm xuyên vào lòng bàn tay, dòng điện chạy từ cổ tay đến ngón tay, thì ngón cái choãi ra là chiều của lực từ tác dụng lên dòng điện
Ta suy ra: