Một khung dây hình vuông cạnh \(5\,\,cm\) đặt trong từ trường đều có cảm ứng từ \(B = {4.10^{ - 4\,}}\,T\), từ thông qua hình vuông đó bằng \({10^{ - 6}}\,\,Wb\). Góc hợp bởi véctơ cảm ứng từ và véc tơ pháp tuyến của hình vuông đó là
Từ thông qua khung dây là:
\(\Phi = BS\cos \alpha \Rightarrow \cos \alpha = \dfrac{\Phi }{{BS}} = \dfrac{\Phi }{{B.{a^2}}} = \dfrac{{{{10}^{ - 6}}}}{{{{4.10}^{ - 4}}.0,{{05}^2}}} = 1 \Rightarrow \alpha = {0^0}\)
Một khung dây hình vuông có cạnh dài \(4\,\,cm\), đặt trong từ trường đều có cảm ứng từ \(B = {4.10^{ - 5}}\,\,T\), mặt phẳng khung dây tạo với các đường sức từ một góc \({60^0}\). Từ thông qua mặt phẳng khung dây có độ lớn là
Từ thông qua mặt phẳng khung dây là:
\(\Phi = BS\cos \alpha = B.{a^2}.\cos \alpha = {4.10^{ - 5}}.{\left( {{{4.10}^{ - 2}}} \right)^2}.\cos {30^0} = 5,{54.10^{ - 8}}\,\,\left( {Wb} \right)\)
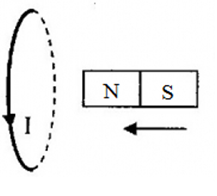
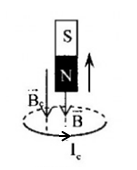
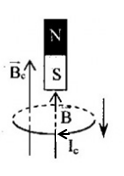
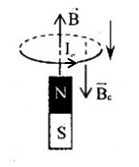
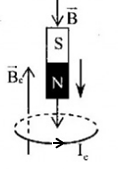
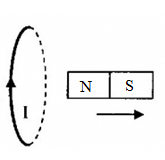
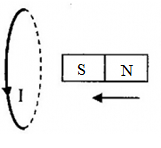
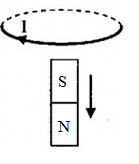
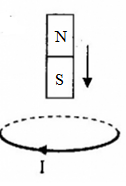
Chiều dòng điện cảm ứng trong vòng dây đúng là?
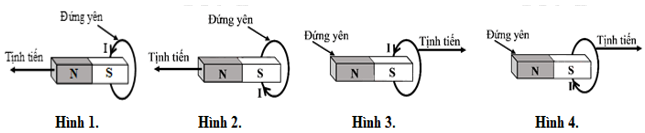
Áp dụng định luật Len-xơ về chiều dòng điện: Dòng điện cảm ứng có chiều sao cho từ trường của nó sinh ra có tác dụng chống lại nguyên nhân sinh ra nó và áp dụng quy tắc nắm tay phải, ta có:
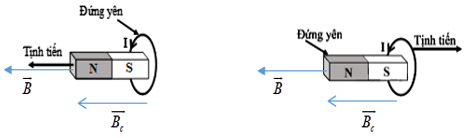
\( \Rightarrow \) Hình 1 và hình 3 - đúng; Hình 2 và hình 4 - sai
Một khung dây phẳng có diện tích \(10\,\,c{m^2}\) đặt trong từ trường đều, mặt phẳng khung dây hợp với đường cảm ứng từ một góc \({30^0}\). Độ lớn từ thông qua khung là \({3.10^{ - 5}}\,\,\left( {Wb} \right)\). Cảm ứng từ có giá trị:
Ta có: \(\alpha = \left( {\overrightarrow B ;\overrightarrow n } \right) = {90^0} - {30^0} = {60^0}\)
Từ thông qua khung dây là:
\(\Phi = BS\cos \alpha \Rightarrow B = \dfrac{\Phi }{{S\cos \alpha }} = \dfrac{{{{3.10}^{ - 5}}}}{{{{10.10}^{ - 4}}.cos{{60}^0}}} = {6.10^{ - 2}}\,\,\left( T \right)\)
Một khung dây dẫn phẳng có diện tích \(12\,\,c{m^2}\) đặt trong từ trường đều cảm ứng từ \(B = {5.10^{ - 2}}\,\,T\), mặt phẳng khung dây hợp với đường cảm ứng từ một góc \({30^0}\). Độ lớn từ thông qua khung là
Góc lệch giữa vecto cảm ứng từ và vecto pháp tuyến của mặt phẳng khung dây là:
\(\alpha = {90^0} - {30^0} = {60^0}\)
Từ thông qua khung dây là:
\(\Phi = BS\cos \alpha = {5.10^{ - 2}}.\left( {{{12.10}^{ - 4}}} \right).\cos {60^0} = {3.10^{ - 5}}\,\,\left( {Wb} \right)\)
Hiện tượng xuất hiện dòng điện cảm ứng trong mạch kín khi từ thông qua mạch biến thiên gọi là:
Hiện tượng xuất hiện dòng điện cảm ứng trong mạch kín khi từ thông qua mạch biến thiên gọi là hiện tượng cảm ứng điện từ
Nhận xét nào sau đây không đúng về cảm ứng từ:
Cảm ứng từ đặc trưng cho từ trường về phương diện tác dụng lực từ → A đúng
Vecto cảm ứng từ tại một điểm có trùng với hướng của từ trường tại điểm đó → B đúng
Cảm ứng từ có đơn vị là Tesla → C đúng
Độ lớn cảm ứng từ không phụ thuộc vào chiều dài đoạn dây dẫn mang dòng điện → D sai
Từ thông qua một mạch điện phụ thuộc vào:
Ta có: \(\Phi = B.S.cos\alpha ;\,\alpha = \left( {\overrightarrow n ;\overrightarrow B } \right)\)
Từ thông qua 1 mạch điện phụ thuộc vào hình dạng và kích thước của mạch điện.
Từ thông qua một diện tích không phụ thuộc yếu tố nào sau đây?
Từ thông qua diện tích \(S\) là: \(\Phi = BS\cos \alpha \Rightarrow \Phi \sim B;S;cos\alpha \)
→ từ thông qua diện tích \(S\) không phụ thuộc vào nhiệt độ môi trường
Một khung dây dẫn hình vuông cạnh \(20\,\,cm\) nằm trong từ trường đều độ lớn \(B = 1,2\,\,T\) sao cho các đường sức vuông góc với mặt khung dây. Từ thông qua khung dây đó là
Các đường sức vuông góc với mặt phẳng khung dây \( \to \alpha = 0\)
Từ thông qua khung dây là:
\(\Phi = BS\cos \alpha = B.{a^2}.cos\alpha = 1,2.0,{2^2}.cos0 = 0,048\,\,\left( {Wb} \right)\)
Một vòng dây dẫn kín, phẳng được đặt trong từ trường đều. Trong khoảng thời gian \(0,04 s\), từ thông qua vòng dây giảm đều từ giá trị \(6.10^{-3}Wb\) về \(0\) thì suất điện động cảm ứng xuất hiện trong vòng dây có độ lớn là
Suất điện động trong vòng dây được xác định bởi biểu thức \(e_{cư}= \dfrac{{|\Delta \Phi |}}{{\Delta t}} = \dfrac{{{|0-{6.10}^{ - 3}|}}}{{0,04}} = 0,15V\)
Một khung dây hình tròn có diện tích \(S = 2c{m^2}\) đặt trong từ trường đều, các đường sức từ xuyên vuông góc với khung dây. Hãy xác định từ thông xuyên qua khung dây. Biết cảm ứng từ \(B = {5.10^{ - 2}}T\)
Ta có, các đường sức từ xuyên vuông góc với khung dây
=> \(\alpha = \left( {\widehat {\overrightarrow n ,\overrightarrow B }} \right) = {0^0}\)
=> Từ thông xuyên qua khung dây: \(\Phi = BScos{0^0} = {5.10^{ - 2}}{.2.10^{ - 4}}.1 = {10^{ - 5}}{\rm{W}}b\)
Một khung dây tròn đặt trong từ trường đều có cảm ứng từ \(B = 0,04T\) sao cho mặt phẳng khung dây vuông góc với các đường sức từ. Từ thông qua khung dây là \(1,{2.10^{ - 4}}{\rm{W}}b\). Bán kính vòng dây là:
Ta có: \(\alpha = (\overrightarrow n ,\overrightarrow B ) = {0^0}\)
Từ thông qua khung: \(\Phi = BSc{\rm{os}}\alpha \to S = \dfrac{\Phi }{{B.c{\rm{os}}{{\rm{0}}^0}}} = \dfrac{{1,{{2.10}^{ - 4}}}}{{0,04}} = {3.10^{ - 3}}\)
Mặt khác, ta có: \(S = \pi {R^2} \to R = \sqrt {\dfrac{S}{\pi }} = \sqrt {\dfrac{{{{3.10}^{ - 3}}}}{\pi }} \approx 0,031m = 3,1cm\)
Một khung dây hình vuông cạnh \(4cm\) đặt trong từ trường đều có cảm ứng từ \(B{\rm{ }} = {\rm{ }}{2.10^{ - 5}}T\). Từ thông qua hình vuông đó bằng \({16.10^{ - 9}}Wb\). Góc hợp bởi giữa véctơ cảm ứng từ và véctơ pháp tuyến của hình vuông đó là:
Ta có:
+ Diện tích của khung: \(S = {a^2} = 0,{04^2} = 1,{6.10^{ - 3}}({m^2})\)
+ Từ thông qua khung:
\(\begin{array}{l}\Phi = BSc{\rm{os}}\alpha \\ \Rightarrow c{\rm{os}}\alpha {\rm{ = }}\dfrac{\Phi }{{BS}} = \dfrac{{{{16.10}^{ - 9}}}}{{{{2.10}^{ - 5}}.1,{{6.10}^{ - 3}}}} = 0,5\\ \Rightarrow \alpha = {60^0}\end{array}\)
Một khung dây hình chữ nhật có chiều dài là \(8cm\), được đặt vuông góc với các đường sức từ của một từ trường đều \(B = 0,02T\). Xác định được từ thông xuyên qua khung dây là \(9,{6.10^{ - 5}}{\rm{W}}b\). Hãy xác định chiều rộng của khung dây trên.
Gọi chiều dài và chiều rộng của hình chữ nhật là a và b
Ta có: \(a = 8cm\)
Diện tích của khung: \(S = a.b\)
Từ thông qua khung: \(\Phi = B{\rm{Scos}}{{\rm{0}}^0} = Bab\)
\( \Rightarrow b = \dfrac{\Phi }{{B.a}} = \dfrac{{9,{{6.10}^{ - 5}}}}{{0,02.0,08}} = 0,06m = 6cm\)
Một khung dây hình tam giác vuông có độ dài cạnh huyền là \(5cm\) và một cạnh góc vuông là \(3cm\). Cả khung dây được đưa vào từ trường đều sao cho các đường sức từ vuông góc với khung dây, từ thông xuyên qua khung dây là \(1,{2.10^{ - 7}}Wb\). Cảm ứng từ B có giá trị:
Cạnh còn lại của tam giác có giá trị:
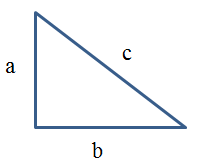
Ta có: \(c = 5cm, a = 3cm\)
Theo định lý Py-ta-go: \(b = \sqrt {{c^2} - {a^2}} = \sqrt {{5^2} - {3^2}} = 4cm\)
Diện tích của tam giác: \(S = \dfrac{1}{2}a.b = \dfrac{1}{2}0,03.0,04 = {6.10^{ - 4}}({m^2})\)
Từ thông qua khung dây: \(\Phi = BSc{\rm{os}}{{\rm{0}}^0} \to B = \dfrac{\Phi }{S} = \dfrac{{1,{{2.10}^{ - 7}}}}{{{{6.10}^{ - 3}}}} = {2.10^{ - 4}}(T)\)
Một khung dây phẳng giới hạn diện tích \(S = 5c{m^2}\) gồm \(20\) vòng dây đặt trong từ trường đều có cảm ứng từ \(B = 0,1T\) sao cho mặt phẳng khung dây hợp với véc tơ cảm ứng từ một góc \({60^0}\). Tính từ thông qua diện tích giới hạn bởi khung dây?
Ta có:
\(\alpha = \left( {\widehat {\overrightarrow n ,\overrightarrow B }} \right) = {30^0}\)
=> Từ thông: \(\Phi = NBS\cos \alpha = 20.0,{1.5.10^{ - 4}}.cos{30^0} = 8,{66.10^{ - 4}}{\rm{W}}b\)
Hình vẽ nào sau đây xác định đúng chiều của dòng điện cảm ứng:
Định luật lenxơ về chiều dòng điện cảm ứng: Dòng điện cảm ứng có chiều sao cho từ trường mà nó sinh ra có tác dụng chống lại nguyên nhân đã sinh ra nó.
A – sai vì, theo quy tắc nắm bàn tay phải Ic phải có chiều như sau:
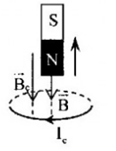
B – sai vì, theo quy tắc nắm bàn tay phải Ic phải có chiều như sau:
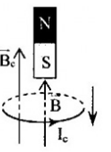
C – sai vì, theo quy tắc nắm bàn tay phải Ic phải có chiều như sau:
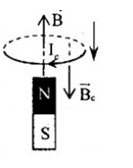
D – đúng
Cách di chuyển nam châm để dòng điện cảm ứng xuất hiện trong mạch như hình là:
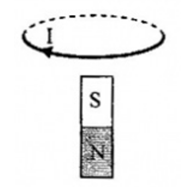
Định luật lenxơ về chiều dòng điện cảm ứng: Dòng điện cảm ứng có chiều sao cho từ trường mà nó sinh ra có tác dụng chống lại nguyên nhân đã sinh ra nó.
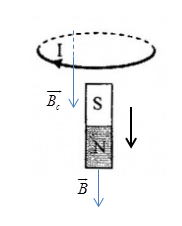
Chọn phương án sai về các cực của nam châm trong các trường hợp sau:
Định luật lenxơ về chiều dòng điện cảm ứng: Dòng điện cảm ứng có chiều sao cho từ trường mà nó sinh ra có tác dụng chống lại nguyên nhân đã sinh ra nó.
B - sai, cực của nam châm phải như sau: