Cho hệ thống như hình. Khi nam châm đi lên thì dòng điện cảm ứng trong vòng dây sẽ có chiều như thế nào? Vòng dây sẽ chuyển động như thế nào?
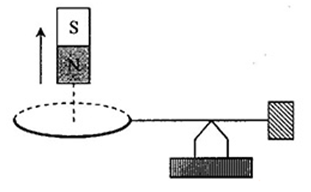
+ Từ trường do nam châm sinh ra có chiều vào S ra N (chiều từ trên xuống dưới)
+ Nam châm đang đi ra xa nên từ cường cảm ứng \(\overrightarrow {{B_c}} \) do khung dây sinh ra có chiều cùng chiều với chiều của từ trường \(\overrightarrow B \) của nam châm từ trên xuống
+ Áp dụng quy tắc nắm tay phải, ta suy ra chiều dòng điện cảm ứng như hình
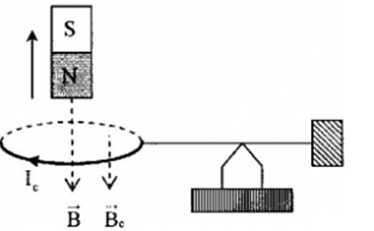
+ Cảm ứng từ do khung dây sinh ra (\(\overrightarrow {{B_c}} \)) có chiều đi vào mặt nam và đi ra mặt bắc
+ Vì mặt nam của khung dây đối diện với cực bắc của nam châm nên chúng sẽ hút nhau
=> Khung dây chuyển động lên trên
Đơn vị đo từ thông là Vêbe \((Wb)\) với \(1 Wb\) bằng
Đơn vị đo từ thông là Vêbe \((Wb)\) với \(1 Wb\) bằng \(1 Tm^2\)
Một khung dây phẳng diện tích \(20c{m^2}\), gồm \(10\) vòng được đặt trong từ trường đều. Véc tơ cảm ứng từ làm thành với mặt phẳng khung dây góc \({30^0}\) và có độ lớn bằng \({2.10^{ - 4}}T\). Người ta làm cho từ trường giảm đều đến 0 trong thời gian \(0,01s\). Tính suất điện động cảm ứng xuất hiện trong khung dây trong thời gian từ trường biến đổi.
Ta có:
+ Từ thông xuất hiện trong khung ban đầu: \({\Phi _1} = N{B_1}Scos{60^0}\) (do véc tơ cảm ứng từ làm thành với mặt phẳng khung dây góc \({30^0}\) => \(\alpha = \left( {\widehat {\overrightarrow n ,\overrightarrow B }} \right) = {90^0} - {30^0} = {60^0}\) )
\( \Rightarrow {\Phi _1} = {10.2.10^{ - 4}}{.20.10^{ - 4}}.cos{60^0} = {2.10^{ - 6}}Wb\)
+ Từ thông lúc sau: \({\Phi _2} = N{B_2}Sc{\rm{os6}}{{\rm{0}}^0} = 0{\rm{W}}b\) (do \({B_2} = 0\) )
=> Suất điện động cảm ứng xuất hiện trong khung dây trong thời gian biến đổi đó: \({e_c} = \left| {\dfrac{{\Delta \Phi }}{{\Delta t}}} \right| = \left| {\dfrac{{{\Phi _2} - {\Phi _1}}}{{\Delta t}}} \right| = \left| {\dfrac{{0 - {{2.10}^{ - 6}}}}{{0,01}}} \right| = {2.10^{ - 4}}V\)
Một khung dây hình chữ nhật kín gồm 10 vòng dây, diện tích mỗi vòng là \(S = 20c{m^2}\) đặt trong một từ trường đều có véc tơ cảm ứng từ \(\overrightarrow B \) hợp với pháp tuyến \(\overrightarrow n \) của mặt phẳng khung dây một góc \(\alpha = {60^0}\), độ lớn cảm ứng từ \(B = 0,04T\), điện trở khung dây \(R = 0,2\Omega \). Tính cường độ dòng điện xuất hiện trong khung dây nếu trong thời gian \(\Delta t = 0,01s\), cảm ứng từ giảm đều từ B đến 0
Trong khoảng thời gian \(\Delta t = 0,01s\), cảm ứng từ giảm đều từ B đến 0
=> Từ thông trong khung cũng giảm từ \({\Phi _1}\) xuống \({\Phi _2}\)
Ta có: \(\left\{ \begin{array}{l}{\Phi _1} = N{B_1}Scos\alpha = 10.0,{04.20.10^{ - 4}}cos{60^0} = {4.10^{ - 4}}{\rm{W}}b\\{\Phi _2} = N{B_2}Scos\alpha = 0Wb\end{array} \right.\)
+ Suất điện động cảm ứng xuất hiện trong khung: \({e_c} = \left| {\dfrac{{\Delta \Phi }}{{\Delta t}}} \right| = \left| {\dfrac{{0 - {{4.10}^{ - 4}}}}{{0,01}}} \right| = 0,04V\)
+ Cường đô dòng điện xuất hiện trong khung: \(i = \dfrac{{{e_c}}}{R} = \dfrac{{0,04}}{{0,2}} = 0,2A\)
Một cuộn dây dẫn dẹt hình tròn, gồm 100 vòng, mỗi vòng có bán kính \(r = 10cm\), mỗi mét chiều dài của dây dẫn có điện trở \({R_0} = 0,5\Omega \). Cuộn dây đặt trong một từ trường đều có véc tở cảm ứng từ B vuông góc với mặt phẳng các vòng dây và có độ lớn \(B = {10^{ - 2}}T\) giảm đều đến 0 trong thời gian \(0,01s\). Xác định công suất tỏa nhiệt trên cuộn dây?
Ta có:
+ Chiều dài 1 vòng dây: \(C = 2\pi r\)
+ Diện tích một vòng dây: \(S = \pi {r^2}\)
=> Chiều dài 100 vòng dây là: \(L = 100C = 200\pi r\)
Theo đầu bài, ta có mỗi mét chiều dài của dây dẫn có điện trở \({R_0} = 0,5\Omega \)
=> Điện trở tổng cộng của 100 vòng dây là: \(R = L.{R_0} = 200\pi r.{R_0} = 200\pi .0,1.0,5 = 10\pi \left( \Omega \right)\)
+ Trong khoảng thời gian \(\Delta t = 0,01s\), cảm ứng từ giảm đều từ B đến 0
=> Từ thông trong khung cũng giảm từ \({\Phi _1}\) xuống \({\Phi _2}\)
Ta có: \(\left\{ \begin{array}{l}{\Phi _1} = N{B_1}Scos\alpha = {100.10^{ - 2}}.\pi {\left( {0,1} \right)^2}cos{0^0} = 0,01\pi {\rm{W}}b\\{\Phi _2} = N{B_2}Scos\alpha = 0Wb\end{array} \right.\)
+ Suất điện động cảm ứng trong cuộn dây: \({e_c} = \left| {\dfrac{{\Delta \Phi }}{{\Delta t}}} \right| = \left| {\dfrac{{0 - 0,01\pi }}{{0,01}}} \right| = \pi \left( V \right)\)
+ Dòng điện cảm ứng trong khung dây: \({i_c} = \dfrac{{\left| {{e_c}} \right|}}{R} = \dfrac{\pi }{{10\pi }} = 0,1 \left( A \right)\)
+ Công suất tỏa nhiệt trên cuộn dây: \(P = i_c^2R = {{0,1}^2}.10\pi = 0,314W\)
Một ống dây dẫn hình trụ dài gồm 1000 vòng dây, mỗi vòng dây có đường kính \(d = 10cm\). Ống dây đó đặt trong từ trường đều, véc tơ cảm ứng từ B song song với trục hình trụ có độ lớn tăng đều với thời gian theo quy luật \(\dfrac{{\Delta B}}{{\Delta t}} = 0,01\left( {T/s} \right)\). Nối hai đầu ống dây vào một tụ điện có \(C = {10^{ - 4}}F\). Hãy tính năng lượng tụ điện
Ta có:
+ Diện tích mỗi vòng dây \(S = \pi \dfrac{{{d^2}}}{4}\)
+ Suất điện động trong ống dây: \(e = \left| {\dfrac{{\Delta \Phi }}{{\Delta t}}} \right| = \left| {\dfrac{{N.\Delta B.S}}{{\Delta t}}} \right| = \left| {N\left( {\pi \dfrac{{{d^2}}}{4}} \right)\dfrac{{\Delta B}}{{\Delta t}}} \right| = \left| {1000.\left( {\pi .\dfrac{{0,{1^2}}}{4}} \right)0,01} \right| = \dfrac{\pi }{{40}}\left( V \right)\)
+ Vì nối hai đầu ống dây vào tụ nên: \({U_C} = e\)
=> Năng lượng trên tụ điện là: \({{\rm{W}}_C} = \dfrac{1}{2}C{U^2} = \dfrac{1}{2}{.10^{ - 4}}{\left( {\dfrac{\pi }{{40}}} \right)^2} = 3,{08.10^{ - 7}}J\)
Một khung phẳng có diện tích \(S = 12c{m^2}\), đặt trong từ trường đều cảm ứng từ \(B = 0,05T\). Vector pháp tuyến của mặt phẳng khung dây hợp với vector cảm ứng từ \(\overrightarrow B \) một góc \({60^0}\). Từ thông qua diện tích S bằng
Từ thông qua khung dây: \(\Phi = NBScos\alpha \)
\(\Phi = 1.0,05.\left( {{{12.10}^{ - 4}}} \right).cos{60^0} = {3.10^{ - 5}}{\rm{W}}b\)
Một vòng dây dẫn kín, phẳng có diện tích 10 cm2. Vòng dây được đặt trong từ trường đều có véctơ cảm ứng từ hợp với véctơ pháp tuyến của mặt phẳng vòng dây một góc 600 và có độ lớn 1,5.10-4 T. Từ thông qua vòng dây này có giá trị là
Từ thông qua vòng dây: \(\Phi = BS\cos \alpha \) với \(\alpha = \left( {\overrightarrow n ;\overrightarrow B } \right)\)
\( \Rightarrow \Phi = 1,{5.10^{ - 4}}{.10.10^{ - 4}}.cos{60^0} = 7,{5.10^{ - 8}}\,\,\left( {{\rm{W}}b} \right)\)
Một hình vuông cạnh 5cm đặt trong từ trường đều có cảm ứng từ \(B = {4.10^{ - 4}}T\), từ thông qua hình vuông đó bằng 10-6 Wb. Tính góc hợp bởi véctơ cảm ứng từ và véctơ pháp tuyến của hình vuông đó :
Diện tích của hình vuông : \(S = 0,{05^2} = 2,{5.10^{ - 3}}\left( {{m^2}} \right)\)
Từ công thức tính từ thông ta có :
\(\begin{array}{l}\Phi = B.S.\cos \left( {\overrightarrow n ;\overrightarrow B } \right)\\ \Rightarrow \cos \left( {\overrightarrow n ;\overrightarrow B } \right) = \dfrac{\Phi }{{B.S}} = \dfrac{{{{10}^{ - 6}}}}{{{{4.10}^{ - 4}}.2,{{5.10}^{ - 3}}}} = 1 \Rightarrow \left( {\overrightarrow n ;\overrightarrow B } \right) = {0^0}\end{array}\)
Một khung dây hình chữ nhật kích thước \(3cm \times 4cm\) đặt trong từ trường đều có cảm ứng từ \(B = {5.10^{ - 4}}T\), vecto cảm ứng từ hợp với mặt phẳng khung dây một góc 300. Từ thông qua khung dây có độ lớn là:
Diện tích của khung dây: \(S = 0,03.0,04 = 1,{2.10^{ - 3}}\,\left( {{m^2}} \right)\)
Vecto cảm ứng từ hợp với mặt phẳng khung dây một góc 300
\( \Rightarrow \,\alpha = \left( {\overrightarrow n ;\overrightarrow B } \right) = {60^0}\)
Từ thông qua khung dây có độ lớn là:
\(\Phi = B.S.\cos \alpha ;\,\alpha = \left( {\overrightarrow n ;\overrightarrow B } \right) = {5.10^{ - 4}}.1,{2.10^{ - 3}}.\cos 60 = {3.10^{ - 7}}{\rm{W}}b\)
Dòng điện cảm ứng IC trong vòng dây có chiều như hình vẽ. Nhận xét nào sau đây đúng?
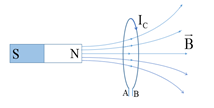
Ta có: Chiều véc-tơ cảm ứng từ do nam châm gây ra có chiều từ trái qua phải.
Áp dụng quy tắc nắm bàn tay phải, từ chiều dòng điện qua vòng dây ta có chiều của véc-tơ cảm ứng từ \(\overrightarrow {{{\rm{B}}_{\rm{C}}}} \) có chiều từ trái qua phải.
\( \Rightarrow \) Nam châm đang chuyển động ra xa cuộn dây
Một diện tích S đặt trong từ trường đều có cảm ứng từ B, góc giữa véctơ cảm ứng từ và véctơ pháp tuyến là \(\alpha \). Từ thông qua diện tích S được tính theo biểu thức:
Từ thông qua một diện tích S đặt trong từ trường đều: \(\Phi = BScos\alpha \)
Đơn vị của từ thông là?
Đơn vị của từ thông: Wb (vêbe)
Một vòng dây phẳng giới hạn diện tích 5cm2 đặt trong từ trường đều cảm ứng từ B = 0,1T. Mặt phẳng vòng dây làm thành với \(\overrightarrow B \) một góc 300. Từ thông qua diện tích trên là:
Ta có:
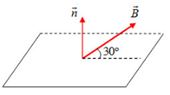
\(\alpha = \left( {\overrightarrow n ,\overrightarrow B } \right) = {90^0} - {30^0} = {60^0}\)
Từ thông qua diện tích S: \(\Phi = BSc{\rm{os}}\alpha = 0,{1.5.10^{ - 4}}.c{\rm{os6}}{{\rm{0}}^0} = 2,{5.10^{ - 5}}({\rm{W}}b)\)
Một khung dây tròn đặt trong từ trường đều có cảm ứng từ B = 0,06T sao cho mặt phẳng khung dây vuông góc với các đường sức từ. Từ thông qua khung dây là 1,2.10-5(Wb). Bán kính vòng dây là:
Ta có: \(\alpha = (\overrightarrow n ,\overrightarrow B ) = {0^0}\)
Từ thông qua khung: \(\Phi = BSc{\rm{os}}\alpha \to S = \dfrac{\Phi }{{B.c{\rm{os}}{{\rm{0}}^0}}} = \dfrac{{1,{{2.10}^{ - 5}}}}{{0,06}} = {2.10^{ - 4}}\)
Mặt khác, ta có: \(S = \pi {R^2} \to R = \sqrt {\dfrac{S}{\pi }} = \sqrt {\dfrac{{{{2.10}^{ - 4}}}}{\pi }} \approx {8.10^{ - 3}}m\)
Một khung dây hình vuông cạnh 5cm đặt trong từ trường đều có cảm ứng từ B = 8.10-4T. Từ thông qua hình vuông đó bằng 10-6 Wb. Góc hợp bởi giữa véctơ cảm ứng từ và véctơ pháp tuyến của hình vuông đó là:
Ta có:
+ Diện tích của khung: \(S = {a^2} = 0,{05^2} = 2,{5.10^{ - 3}}({m^2})\)
+ Từ thông qua khung: \(\Phi = BSc{\rm{os}}\alpha \to c{\rm{os}}\alpha {\rm{ = }}\dfrac{\Phi }{{BS}} = \dfrac{{{{10}^{ - 6}}}}{{{{8.10}^{ - 4}}.2,{{5.10}^{ - 3}}}} = 0,5 \to \alpha = {60^0}\)
Một khung dây hình chữ nhật có chiều dài $25cm$, được đặt vuông góc với các đường sức từ của một từ trường đều $B = 4.10^{-3}T$. Biết từ thông qua hình chữ nhật đó bằng ${10^{-4}}Wb$. Chiều rộng của khung dây trên là:
Gọi chiều dài và chiều rộng của hình chữ nhật là a và b
Ta có:
\(a = 25cm\)
Từ thông qua khung: \(\Phi = B{\rm{Scos}}{{\rm{0}}^0} = Bab \to b = \dfrac{\Phi }{{B.a}} = \dfrac{{{{10}^{ - 4}}}}{{{{4.10}^{ - 3}}.0,25}} = 0,1m = 10cm\)
Một khung dây hình tam giác vuông có độ dài cạnh huyền là 10cm và một cạnh góc vuông là 8cm. Cả khung dây được đưa vào từ trường đều sao cho các đường sức từ vuông góc với khung dây, từ thông xuyên qua khung dây là 1,2.10-7Wb. Cảm ứng từ B có giá trị:
Cạnh còn lại của tam giác có giá trị:
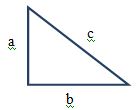
Ta có: c = 10cm, b = 8cm
Theo định lý Py-ta-go: \(a = \sqrt {{c^2} - {b^2}} = \sqrt {{{10}^2} - {8^2}} = 6cm\)
Diện tích của tam giác: \(S = \frac{1}{2}a.b = \frac{1}{2}0,06.0,08 = 2,{4.10^{ - 3}}({m^2})\)
Từ thông qua khung dây: \(\Phi = BSc{\rm{os}}{{\rm{0}}^0} \to B = \frac{\Phi }{S} = \frac{{1,{{2.10}^{ - 7}}}}{{2,{{4.10}^{ - 3}}}} = {5.10^{ - 5}}(T)\)
Một khung dây có chiều dài l = 40cm. Gồm 4000 vòng, cho dòng điện I = 10A chạy trong ống dây. Đặt đối diện với ống dây một khung dây hình vuông có cạnh a = 5cm. Từ thông xuyên qua khung dây là:
Ta có cảm ứng từ gây ra bởi ống dây: \(B = 4\pi {.10^{ - 7}}\frac{{NI}}{l} = 4\pi {.10^{ - 7}}\frac{{4000.10}}{{0,4}} = 0,1257(T)\)
Diện tích của khung dây: \(S = {a^2} = 0,{05^2} = 2,{5.10^{ - 3}}({m^2})\)
Từ thông qua khung dây: \(\Phi = BSc{\rm{os}}{0^0} = 0,1257.2,{5.10^{ - 3}} = 3,{14.10^{ - 4}}({\rm{W}}b)\)
Phát biểu nào sau đây không đúng ?
Ta có:
+ Dòng điện xuất hiện khi có sự biến đổi từ thông qua mạch điện kín gọi là dòng điện cảm ứng
+ từ thông qua một diện tích S:
A- sai vì khi khung quay quanh trục song song với các đường cảm ứng từ thì từ thông qua khung dây luôn bằng 0 => không có dòng điện cảm ứng
B, C, D - đúng

