Dòng điện \(I = 1\,\,\left( A \right)\) chạy trong dây dẫn thẳng dài. Cảm ứng từ tại điểm \(M\) cách dây dẫn \(10\,\,\left( {cm} \right)\) có độ lớn là:
Cảm ứng từ tại điểm \(M\) là:
\(B = {2.10^{ - 7}}\frac{I}{r} = {2.10^{ - 7}}.\dfrac{1}{{0,1}} = {2.10^{ - 6}}\,\,\left( T \right)\)
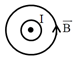
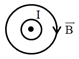
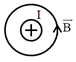
Trong các hình vẽ sau, hình vẽ nào biểu diễn đúng hướng của đường cảm ứng từ của dòng điện trong dây dẫn thẳng dài vuông góc với mặt phẳng hình vẽ:
Áp dụng quy tắc nắm tay phải, ta có:
Dòng điện hướng từ trong ra ngoài, từ trường hướng ngược chiều kim đồng hồ → A đúng, B sai
Dòng điện hương từ ngoài vào trong, từ trường hướng cùng chiều kim đồng hồ → C sai
Tại một điểm cách dây dẫn thẳng dài vô hạn mang dòng điện \(5 A\) có cảm ứng từ là \(4.10^{-4}T\). Nếu cường độ dòng điện trong dây dẫn tăng thêm \(20 A\) thì cảm ứng từ tại điểm đó có giá trị là
Cảm ứng từ của dây dẫn thẳng dài \(B = {2.10^{ - 7}}\dfrac{I}{r}\)
\(\dfrac{{{B_2}}}{{{B_1}}} = \dfrac{{{I_2}}}{{{I_1}}} = \dfrac{{5 + 20}}{5} = 5 \to {B_2} = 5{B_1} = {2.10^{ - 3}}(T)\)
Một dây dẫn uốn thành vòng tròn có bán kính \(3,14\,\,cm\) được đặt trong không khí. Cho dòng điện không đổi có cường độ \(2\,\,A\) chạy trong vòng dây. Cảm ứng từ do dòng điện gây ra tại tâm vòng dây có độ lớn là
Cảm ứng từ do dòng điện gây ra tại tâm vòng dây là:
\(B = 2\pi {.10^{ - 7}}\dfrac{{NI}}{R} = 2\pi {.10^{ - 7}}.\dfrac{{1.2}}{{3,{{14.10}^{ - 2}}}} = {4.10^{ - 5}}\,\,\left( T \right)\)
Một dây dẫn thẳng dài có dòng điện chạy qua với cường độ \(I{\rm{ }} = {\rm{ }}2,5A\). Cảm ứng từ tại điểm M cách dây dẫn một đoạn \(r{\rm{ }} = {\rm{ }}8cm\) có giá trị là:
Cảm ứng từ tại M là: \(B = {2.10^{ - 7}}\dfrac{I}{r} = {2.10^{ - 7}}\dfrac{{2,5}}{{{{8.10}^{ - 2}}}} = 6,{25.10^{ - 6}}T\)
Một dây dẫn thẳng dài vô hạn mang dòng điện 0,5A đặt trong không khí. Tính cảm ứng từ tại M cách dòng điện 4cm.
Cảm ứng từ tại M là: \(B = {2.10^{ - 7}}\dfrac{I}{r} = {2.10^{ - 7}}\dfrac{{0,5}}{{{{4.10}^{ - 2}}}} = 2,{5.10^{ - 6}}T\)
Một dây dẫn thẳng dài vô hạn mang dòng điện 0,5A đặt trong không khí. Cảm ứng từ tại điểm N là \({10^{ - 6}}T\). Tính khoảng cách từ N đến dòng điện.
Ta có:
Cảm ứng từ tại N là: \({B_N} = {2.10^{ - 7}}\dfrac{I}{r}\)
\( \Rightarrow r = \dfrac{{{{2.10}^{ - 7}}I}}{{{B_N}}} = \dfrac{{{{2.10}^{ - 7}}.0,5}}{{{{10}^{ - 6}}}} = 0,1m = 10cm\)
Một khung dây tròn bán kính \(R = 4\,\,cm\) gồm \(10\) vòng dây. Dòng điện chạy trong mỗi vòng dây có cường độ \(I = 0,3\,\,\left( A \right)\). Cảm ứng từ tại tâm của khung là:
Cảm ứng từ tại tâm của khung dây là:
\(B = 2\pi {.10^{ - 7}}\frac{{NI}}{R} = 2\pi {.10^{ - 7}}.\frac{{10.0,3}}{{{{4.10}^{ - 2}}}} = 4,{7.10^{ - 5}}\,\,\left( T \right)\)
Hai dòng điện thẳng dài, đặt song song ngược chiều, cách nhau 20cm trong không khí có \({I_1} = 12A\), \({I_2} = 15A\). Xác định cảm ứng từ tổng hợp tại điểm M cách \({I_1}\) \(15cm\) và cách \({I_2}\) là \(5cm\)?
Giả sử hai dây dẫn được đặt vuông góc với mặt phẵng hình vẽ, dòng I1 đi vào tại A, dòng I2 đi ra tại B thì các dòng điện \({I_1}\) và \({I_2}\) gây ra tại M các véc tơ cảm ứng từ \(\mathop {{B_1}}\limits^ \to \) và \(\mathop {{B_2}}\limits^ \to \) có phương chiều như hình vẽ:
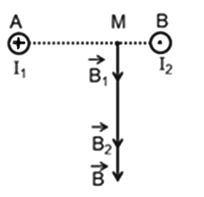
Có độ lớn: \(\left\{ \begin{array}{l}{B_1} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_1}}}{{AM}} = {2.10^{ - 7}}\dfrac{{12}}{{{{15.10}^{ - 2}}}}{\rm{ = }}1,{6.10^{ - 5}}T\\{B_2} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_2}}}{{BM}} = {2.10^{ - 7}}\dfrac{{15}}{{{{5.10}^{ - 2}}}}{\rm{ = }}{6.10^{ - 5}}T\end{array} \right.\)
Cảm ứng từ tổng hợp tại M là: \(\mathop B\limits^ \to = \mathop {{B_1}}\limits^ \to + \mathop {{B_2}}\limits^ \to \) .
Vì \(\mathop {{B_1}}\limits^ \to \) và \(\mathop {{B_2}}\limits^ \to \) cùng phương, cùng chiều \( \Rightarrow B = {B_1} + {B_2} = 1,{6.10^{ - 5}} + {6.10^{ - 5}} = 7,{6.10^{ - 5}}T\)
Một dây dẫn có dòng điện chạy qua uốn thành một vòng dây tròn. Tại tâm vòng tròn, cảm ứng từ sẽ giảm khi
Cảm ứng từ tại tâm dòng điện tròn: \(B = 2\pi {.10^{ - 7}}\frac{I}{r} \Rightarrow \left\{ \begin{array}{l}B \sim I\\B \sim \frac{1}{r}\end{array} \right.\)
→ cảm ứng từ B giảm khi cường độ dòng điện giảm hoặc đường kính vòng dây tăng
Cho dây dẫn thẳng dài mang dòng điện. Khi điểm ta xét gần dây hơn 2 lần và cường độ dòng điện tăng 2 lần thì độ lớn cảm ứng từ
Cảm ứng từ do dòng điện chạy trong dây dẫn thẳng gây ra là: \(I = {2.10^{ - 7}}\frac{I}{r}\)
Khi xét điểm gần dây hơn \(2\) lần và cường độ dòng điện tăng \(2\) lần, độ lớn cảm ứng từ là:
\(I' = {2.10^{ - 7}}\frac{{I'}}{{r'}} = {2.10^{ - 7}}.\frac{{2I}}{{\frac{r}{2}}} = {4.2.10^{ - 7}}\frac{I}{r} = 4I\)
Hai dòng điện thẳng dài, đặt song song cùng chiều cách nhau \(10cm\) trong không khí có \({I_1} = 9A\) , \({I_2} = 12A\). Xác định cảm ứng từ tổng hợp tại điểm M cách \({I_1}\) là \(6cm\) và cách \({I_2}\) là \(8cm\)?
Giả sử hai dây dẫn được đặt vuông góc với mặt phẵng hình vẽ, dòng \({I_1}\) đi vào tại A, dòng I2 đi vào tại B. Tam giác AMB vuông tại M. Các dòng điện \({I_1}\) và \({I_2}\) gây ra tại M các véc tơ cảm ứng từ \(\mathop {{B_1}}\limits^ \to \) và \(\mathop {{B_2}}\limits^ \to \) có phương chiều như hình vẽ:
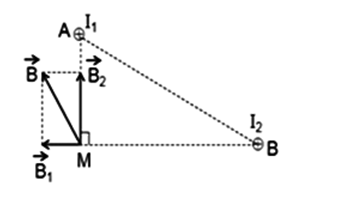
Có độ lớn:
\(\left\{ \begin{array}{l}{B_1} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_1}}}{{AM}} = {\rm{ 2}}{\rm{.1}}{{\rm{0}}^{ - 7}}\dfrac{9}{{0,06}} = {3.10^{ - 5}}T\\{B_2} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_2}}}{{BM}} = {\rm{ 2}}{\rm{.1}}{{\rm{0}}^{ - 7}}\dfrac{{12}}{{0,08}} = {3.10^{ - 5}}T\end{array} \right.\)
Cảm ứng từ tổng hợp tại M là: \(\mathop B\limits^ \to = \mathop {{B_1}}\limits^ \to + \mathop {{B_2}}\limits^ \to \) có phương chiều như hình vẽ và có độ lớn:
\(B = \sqrt {B_1^2 + B_2^2} = \sqrt {{{({{3.10}^{ - 5}})}^2} + {{({{3.10}^{ - 5}})}^2}} = 3\sqrt 2 {.10^{ - 5}}T\)
Hai dòng điện thẳng dài, đặt song song ngược chiều cách nhau \(20cm\) trong không khí có \({I_1} = {I_2} = 12A\). Xác định cảm ứng từ tổng hợp tại điểm M cách \({I_1}\) là \(16cm\) và cách \({I_2}\) là \(12cm\).
Giả sử hai dây dẫn được đặt vuông góc với mặt phẵng hình vẽ, dòng \({I_1}\) đi vào tại A, dòng I2 đi ra tại B.
Tam giác AMB vuông tại M. Các dòng điện \({I_1}\) và \({I_2}\) gây ra tại M các véc tơ cảm ứng từ \(\mathop {{B_1}}\limits^ \to \) và \(\mathop {{B_2}}\limits^ \to \) có phương chiều như hình vẽ:
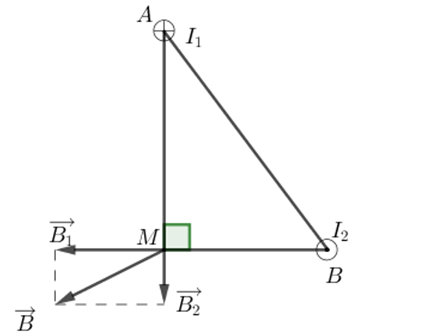
Có độ lớn: \(\left\{ \begin{array}{l}{B_1} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_1}}}{{AM}} = {\rm{ 2}}{\rm{.1}}{{\rm{0}}^{ - 7}}\dfrac{{12}}{{{{16.10}^{ - 2}}}} = 1,{5.10^{ - 5}}T\\{B_2} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_2}}}{{BM}} = {\rm{ 2}}{\rm{.1}}{{\rm{0}}^{ - 7}}\dfrac{{12}}{{{{12.10}^{ - 2}}}} = {2.10^{ - 5}}T\end{array} \right.\)
Cảm ứng từ tổng hợp tại M là:\(\mathop B\limits^ \to = \mathop {{B_1}}\limits^ \to + \mathop {{B_2}}\limits^ \to \) có phương chiều như hình vẽ và có độ lớn:
\(B = \sqrt {B_1^2 + B_2^2} = \sqrt {{{(1,{{5.10}^{ - 5}})}^2} + {{({{2.10}^{ - 5}})}^2}} = 2,{5.10^{ - 5}}T\)
Hai dòng điện thẳng dài, đặt song song ngược chiều, cách nhau \(20cm\) trong không khí có \({I_1} = {I_2} = 9A\). Xác định cảm ứng từ tổng hợp tại điểm M cách đều \({I_1}\) và \({I_2}\) một khoảng \(30cm\).
Giả sử hai dây dẫn được đặt vuông góc với mặt phẵng hình vẽ, dòng \({I_1}\) đi vào tại A, dòng \({I_2}\) đi ra tại B. Các dòng điện \({I_1}\) và \({I_2}\) gây ra tại M các véc tơ cảm ứng từ \(\mathop {{B_1}}\limits^ \to \)và \(\mathop {{B_2}}\limits^ \to \) có phương chiều như hình vẽ:
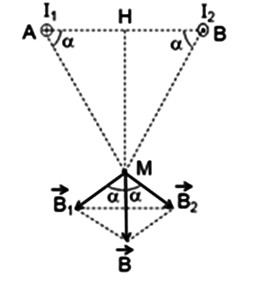
Ta có: \(AM = BM = 30cm = 0,3m\)
Cảm ứng từ do các dòng \({I_1},{I_2}\) gây ra tại M
\({B_1} = {B_2} = {2.10^{ - 7}}\dfrac{{{I_1}}}{{AM}} = {2.10^{ - 7}}\dfrac{9}{{0,3}} = {6.10^{ - 6}}T\)
Từ hình, ta có: \(\left\{ \begin{array}{l}AH = \dfrac{{AB}}{2} = \dfrac{{20}}{2} = 10cm = 0,1m\\cos\alpha = \dfrac{{AH}}{{AM}}\end{array} \right.\)
Cảm ứng từ tổng hợp tại M là: \(\mathop B\limits^ \to = \mathop {{B_1}}\limits^ \to + \mathop {{B_2}}\limits^ \to \) có phương chiều như hình vẽ và có độ lớn:
\(\begin{array}{l}B = {B_1}cos\alpha + {B_2}cos\alpha \\ = 2{B_1}cos\alpha = 2{B_1}\dfrac{{AH}}{{AM}}\\ = {2.6.10^{ - 6}}.\dfrac{{0,1}}{{0,3}} = {4.10^{ - 6}}T\end{array}\)
Hai dòng điện thẳng dài đặt song song cùng chiều, cách nhau \(d = 12cm\) trong không khí có \({I_2} = {I_1} = I = 10A\). Xác định cảm ứng từ tổng hợp tại điểm M cách đều \({I_1}\) và \({I_2}\) một khoảng x. Hãy xác định x để độ lớn cảm ứng từ tổng hợp do hai dòng điện gây ra đạt giá trị cực đại. Tính giá trị cực đại đó
Giả sử hai dây dẫn được đặt vuông góc với mặt phẵng hình vẽ, dòng \({I_1}\) đi vào tại A, dòng \({I_2}\) đi vào tại B. Các dòng điện \({I_1}\) và \({I_2}\) gây ra tại M các véc tơ cảm ứng từ \(\mathop {{B_1}}\limits^ \to \) và \(\mathop {{B_2}}\limits^ \to \) có phương chiều như hình vẽ:
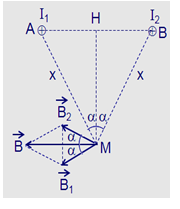
Có độ lớn: \({B_1} = {B_2} = {2.10^{ - 7}}\dfrac{I}{x}\)
Từ hình ta có: \(\left\{ \begin{array}{l}AH = \dfrac{{12}}{2} = 6cm = 0,06m\\HM = \sqrt {A{M^2} - A{H^2}} = \sqrt {{x^2} - 0,{{06}^2}} \\cos\alpha = \dfrac{{HM}}{{AM}}\end{array} \right.\)
Cảm ứng từ tổng hợp tại M là:
\(\mathop B\limits^ \to = \mathop {{B_1}}\limits^ \to + \mathop {{B_2}}\limits^ \to \) có phương chiều như hình vẽ và có độ lớn:
\(\begin{array}{l}B = 2{B_1}cos\alpha = {2.2.10^{ - 7}}\dfrac{I}{x}\dfrac{{HM}}{{AM}}\\ = {4.10^{ - 7}}.\dfrac{{10}}{x}\dfrac{{\sqrt {{x^2} - 0,{{06}^2}} }}{x}\\ = {4.10^{ - 6}}\dfrac{{\sqrt {{x^2} - 0,{{06}^2}} }}{{{x^2}}}\end{array}\)
Nhận thấy, B đạt cực đại khi \(\dfrac{{\sqrt {{x^2} - 0,{{06}^2}} }}{{{x^2}}}\) đạt cực đại:
Ta có:
\(\begin{array}{l}\dfrac{{\sqrt {{x^2} - 0,{{06}^2}} }}{{{x^2}}} = \sqrt {\dfrac{{{x^2} - 0,{{06}^2}}}{{{x^4}}}} = \sqrt {\dfrac{1}{{{x^2}}}\left( {1 - \dfrac{{0,{{06}^2}}}{{{x^2}}}} \right)} \\ = \sqrt {\dfrac{1}{{0,{{06}^2}}}\dfrac{{0,{{06}^2}}}{{{x^2}}}\left( {1 - \dfrac{{0,{{06}^2}}}{{{x^2}}}} \right)} = \dfrac{1}{{0,06}}\sqrt {\dfrac{{0,{{06}^2}}}{{{x^2}}}\left( {1 - \dfrac{{0,{{06}^2}}}{{{x^2}}}} \right)} \end{array}\)
Do \(d < x \to 1 - \dfrac{{0,{{06}^2}}}{{{{\rm{x}}^2}}} > 0\)
Áp dụng BĐT cosi (\(\sqrt {ab} \le \dfrac{{a + b}}{2}\) ) ta có: \(\sqrt {\dfrac{{0,{{06}^2}}}{{{x^2}}}\left( {1 - \dfrac{{0,{{06}^2}}}{{{x^2}}}} \right)} \le \dfrac{{\dfrac{{0,{{06}^2}}}{{{x^2}}} + 1 - \dfrac{{0,{{06}^2}}}{{{x^2}}}}}{2} = \dfrac{1}{2}\)
Dấu “ = ” xảy ra khi: \(\dfrac{{0,{{06}^2}}}{{{x^2}}} = 1 - \dfrac{{0,{{06}^2}}}{{{x^2}}} \Rightarrow x = 6\sqrt 2 {.10^{ - 2}}m\)
Khi đó \({B_{max}} = {4.10^{ - 6}}\dfrac{1}{{0,06}}.\dfrac{1}{2} = 3,{33.10^{ - 5}}T\)
Hai dây dẫn thẳng dài vô hạn song song cách nhau khoảng \(8cm\) trong không khí, có dòng điện ngược chiều \({I_1} = {I_2} = 10A\) đi qua. Tính cảm ứng từ tại điểm M cách mỗi dây \(4cm\)
Gọi \(\overrightarrow {{B_1}} ,\overrightarrow {{B_2}} \) lần lượt là cảm ứng từ do dòng \({I_1}\) và \({I_2}\) gây ra tại M.
Áp dụng quy tắc bàn tay phải ta có:
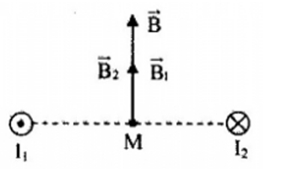
Ta có: \(\left\{ \begin{array}{l}{B_1} = {2.10^{ - 7}}\dfrac{{{I_1}}}{{{r_1}}} = {2.10^{ - 7}}\dfrac{{10}}{{0,04}} = {5.10^{ - 5}}T\\{B_2} = {2.10^{ - 7}}\dfrac{{{I_2}}}{{{r_2}}} = {2.10^{ - 7}}\dfrac{{10}}{{0,04}} = {5.10^{ - 5}}T\end{array} \right.\)
Cảm ứng từ tổng hợp tại M: \(\overrightarrow B = \overrightarrow {{B_1}} + \overrightarrow {{B_2}} \)
Lại có: \(\overrightarrow {{B_1}} \uparrow \uparrow \overrightarrow {{B_2}} \)
\( \Rightarrow B = {B_1} + {B_2} = {5.10^{ - 5}} + {5.10^{ - 5}} = {10^{ - 4}}T\)
Hai dòng điện thẳng dài đặt trong không khí, trùng với hai trục tọa độ vuông góc xOy. Dòng \({I_1} = 6A\) ngược chiều với chiều dương trục Ox, dòng \({I_2} = 9A\) cùng chiều với chiều dương trục Oy. Tính cảm ứng từ tổng hợp tại điểm M có tọa độ \(M\left( {4cm,6cm} \right)\)
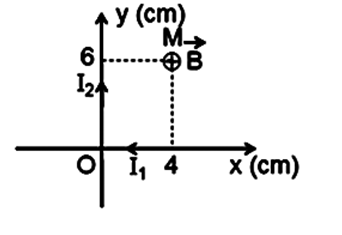
Ta có:
+ Dòng \({I_1}\) gây ra tại M véc tơ cảm ứng từ \(\mathop {{B_1}}\limits^ \to \) vuông góc với mặt phẵng xOy, hướng từ ngoài vào, có độ lớn: \({B_1} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_1}}}{y} = {2.10^{ - 7}}\dfrac{6}{{0,06}} = {2.10^{ - 5}}T\)
+ Dòng \({I_2}\) gây ra tại M véc tơ cảm ứng từ \(\mathop {{B_2}}\limits^ \to \) vuông góc với mặt phẵng xOy, hướng từ ngoài vào, có độ lớn: \({B_2} = {\rm{ }}{2.10^{ - 7}}\dfrac{{{I_2}}}{x} = {2.10^{ - 7}}.\dfrac{9}{{0,04}} = 4,{5.10^{ - 5}}T\)
Cảm ứng từ tổng hợp tại M: \(\overrightarrow B = \overrightarrow {{B_1}} + \overrightarrow {{B_2}} \)
Ta có:
\(\begin{array}{l}\overrightarrow {{B_1}} \uparrow \uparrow \overrightarrow {{B_2}} \\ \Rightarrow B = {B_1} + {B_2} = {2.10^{ - 5}} + 4,{5.10^{ - 5}} = 6,{5.10^{ - 5}}T\end{array}\)
Một vòng dây tròn đặt trong chân không có bán kính \(R=20cm\) mang dòng điện \(I=50A\). Cảm ứng từ tại tâm vòng dây có độ lớn là:
Độ lớn cảm ứng từ tại tâm vòng dây:
\(B = 2\pi {.10^{ - 7}}\dfrac{I}{R} = 2\pi {.10^{ - 7}}.\dfrac{{50}}{{{{20.10}^{ - 2}}}} = 5\pi {.10^{ - 5}} \approx 15,{7.10^{ - 5}}T\)
Dùng một dây uốn thành vòng tròn và cho dòng điện cường độ \(I = 10A\) chạy qua vòng dây, cảm ứng từ do dòng điện gây ra tại tâm của vòng tròn có giá trị là \(4\pi {.10^{ - 5}}T\). Hãy xác định bán kính của vòng dây trên?
Ta có:
Cảm ứng từ tại tâm vòng dây: \(B = 2\pi {.10^{ - 7}}\dfrac{I}{r}\)
=> Bán kính của vòng dây: \(r = \dfrac{{2\pi {{.10}^{ - 7}}I}}{B} = \dfrac{{2\pi {{.10}^{ - 7}}.10}}{{4\pi {{.10}^{ - 5}}}} = 0,05m = 5cm\)
Một dây dẫn rất dài được căng thẳng, trong đó có một đoạn nhỏ được uốn thành vòng tròn bán kính 1,5cm (như hình dưới). Cho dòng điện cường độ \(I = 3A\) chạy trong dây dẫn. Xác định véc tơ cảm ứng từ tại tâm O của vòng dây.
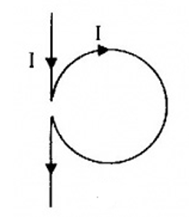
+ Gọi \(\overrightarrow {{B_1}} ,\overrightarrow {{B_2}} \) lần lượt là cảm ứng từ gây bởi phần dòng điện thẳng dài và phần dòng điện tròn tại tâm O
+ Dựa vào quy tắc nắm bàn tay phải, ta suy ra véc tơ \(\overrightarrow {{B_1}} \) có chiều từ trong ra, véc tơ \(\overrightarrow {{B_2}} \) có chiều hướng vào trong
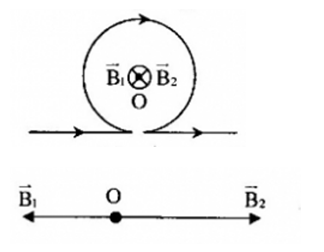
Ta có: \(\left\{ \begin{array}{l}{B_1} = {2.10^{ - 7}}\dfrac{I}{R}\\{B_2} = 2\pi {.10^{ - 7}}\dfrac{I}{R}\end{array} \right.\)
Cảm ứng từ tổng hợp tại O: \(\overrightarrow B = \overrightarrow {{B_1}} + \overrightarrow {{B_2}} \)
Vì \(\overrightarrow {{B_1}} \uparrow \downarrow \overrightarrow {{B_2}} \Rightarrow B = \left| {{B_1} - {B_2}} \right|\)
Ta có \({B_2} > {B_1} \Rightarrow \overrightarrow B \) có chiều là chiều của \(\overrightarrow {{B_2}} \) và có độ lớn:
\(\begin{array}{l}B = {B_2} - {B_1} = {2.10^{ - 7}}\dfrac{I}{R}\left( {\pi - 1} \right)\\ = {2.10^{ - 7}}\dfrac{3}{{1,{{5.10}^{ - 2}}}}\left( {\pi - 1} \right)\\ \approx 8,{57.10^{ - 5}}T\end{array}\)