Kính hiển vi

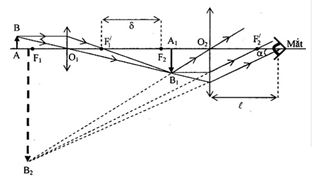
+ Ta có độ dài quang học: \(\delta  = \ell  - ({f_1} + {f_2}) = 17 - (1 + 4) = 12(cm)\)

+  Đ = OC_C =25 (cm) là khoảng cực cận của mắt.

=> Độ bội giác của kính khi ngắm chừng ở vô cực là: \({G_\infty } = \dfrac{{12.25}}{{1.4}} = 75\)

A - sai vì tiêu bản phải nằm ngoài khoảng O₁F₁ và gần F₁

B - đúng

C – sai vì: ảnh A₁B₁ là ảnh thật

D – sai vì: ảnh cuối cùng A₂B₂ là ảnh ảo

+ Theo bài ra: \({f_1} = 4mm = 0,4cm;{\rm{ }}{f_2} = 20mm = 2cm\)

Vật cách vật kính khoảng \(d = 5mm = 0,5cm\)

+ Theo công thức thấu kính, vị trí ảnh qua vật kính là: \(d' = \dfrac{{d{f_1}}}{{d - {f_1}}} = \dfrac{{0,5.0,4}}{{0,5 - 0,4}} = 2cm\)

+ Theo đề bài, ta có: \({k_1} = 40;{\rm{ }}{f_2} = 2cm\) và \(D = 10cm\)

+ Số bội giác của kính khi ngắm chừng ở vô cực là: \({G_\infty } = {k_1}\dfrac{D}{{{f_2}}} = 40.\dfrac{{10}}{2} = 200\)

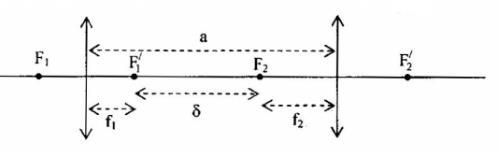
Ta có, khoảng cách giữa hai thấu kính \({O_1}{O_2} = a = 17cm\)

=> Độ dài quang học của kính hiển vi: \(\delta  = {O_1}{O_2} - \left( {{f_1} + {f_2}} \right) = 17 - \left( {1 + 4} \right) = 12cm\)

+ Số bội giác của kính khi ngắm chừng ở vô cực: \({G_\infty } = \dfrac{{\delta D}}{{{f_1}{f_2}}} = \dfrac{{12.25}}{{1.4}} = 75\)

Theo bài ra: \({f_1} = 5mm = 0,5cm;{\rm{ }}{f_2} = 20mm = 2cm;{\rm{ }}\delta  = 120mm = 12cm\) và \(D = 25cm\)

Khi ngắm chừng ở vô cực thì ảnh của vật qua vật kính tại tiêu diện của thị kính \({d_1}' = \delta  + {f_1} = 120 + 5 = 125mm = 12,5cm\)

\( \to {d_1} = \dfrac{{{d_1}'{f_1}}}{{{d_1}' - {f_1}}} = \dfrac{{12,5.0,5}}{{12,5 - 0,5}} = 0,52cm\)

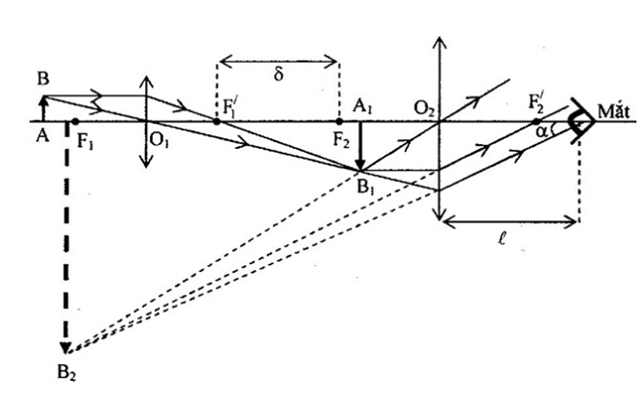
+ Quá trình tạo ảnh của kính hiển vi giống như quá trình tạo ảnh qua hệ hai thấu kính ghép đồng trục và được tóm tắt qua sơ đồ sau:

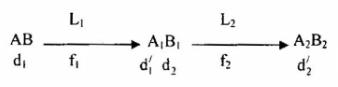
+ Khi ngắm chừng ảnh \({A_2}{B_2}\) ở điểm cực viễn của mắt, ta có:

\({d_2}' = \infty  \Rightarrow {d_2} = {f_2} = 2cm\)

\({d_1}' = \overline {{O_1}{A_1}}  = a - {d_2} = 16 - 2 = 14cm\)

\( \Rightarrow {d_1} = \overline {{O_1}A}  = \dfrac{{{d_1}'{f_1}}}{{{d_1}' - {f_1}}} = \dfrac{{14.0,8}}{{14 - 0,8}} = \dfrac{{28}}{{33}}\)

+ Mắt trông ảnh \({A_2}{B_2}\) dưới góc trông \(\alpha \). Để phân biệt được hai điểm A, B qua kính tức phân biệt ảnh 2 \({A_2}{B_2}\) của nó, muốn vậy \(\alpha  \ge \varepsilon \)

+ Ta có, \(\alpha  \approx \tan \alpha  = \dfrac{{{A_2}{B_2}}}{{\left| {{d_2}'} \right|}} \ge \varepsilon \) 

\( \Rightarrow {A_2}{B_2} \ge \left| {{d_2}'} \right|\varepsilon \)  (1)

+ Mặt khác, \(\dfrac{{{A_2}{B_2}}}{{AB}} = \dfrac{{{A_2}{B_2}}}{{{A_1}{B_1}}}\dfrac{{{A_1}{B_1}}}{{AB}} = \left| {\dfrac{{{d_2}'}}{{{d_2}}}} \right|\left| {\dfrac{{{d_1}'}}{{{d_1}}}} \right|\)

\( \Rightarrow {A_2}{B_2} = \left| {\dfrac{{{d_2}'}}{{{d_2}}}} \right|\left| {\dfrac{{{d_1}'}}{{{d_1}}}} \right|AB\)  (2)

Từ (1) và (2) ta suy ra: \(\left| {\dfrac{{{d_2}'}}{{{d_2}}}} \right|\left| {\dfrac{{{d_1}'}}{{{d_1}}}} \right|AB \ge \left| {{d_2}'} \right|\varepsilon \)

\( \Rightarrow AB \ge \varepsilon \left| {\dfrac{{{d_2}{d_1}}}{{{d_1}'}}} \right| = \dfrac{1}{{3500}}\dfrac{{2.\dfrac{{28}}{{33}}}}{{24}} = {3,46.10^{ - 5}}\left( {cm} \right)\)

Cấu tạo của kính hiển vi:

+ Vật kính là một thấu kính hội tụ (hoặc hệ thấu kính có tác dụng như thấu kính hội tụ) có tiêu cự rất nhỏ (cỡ vài mm).

+ Thị kính là kính lúp dùng để quan sát ảnh của vật tạo bởi vật kính.

Vật kính và thị kính gắn đồng trục ở hai đầu một ống hình trụ

=> A, C, D - sai

B - đúng

Ta có: Ngắm chừng qua kính hiển vi:

+ Vật (tiêu bản) đặt cố định trên giá.

+ Mắt đặt sau thị kính để quan sát ảnh.

+ Nâng dần ống kính xa dần vật sao cho ảnh ảo cuối cùng của vật nằm trong khoảng nhìn rõ của mắt.

=> A, B, D - sai

C - đúng

Ta có: Số bội giác của kính hiển vi khi ngắm chừng ở vô cực: \({G_\infty } = \left| {{k_1}} \right|{G_2} = \frac{{\delta Đ}}{{{f_1}{f_2}}}\)

=> số bội giác tỉ lệ nghịch với  (tiêu cự của vật kính và tiêu cự của thị kính)

Khi sử dụng kính hiển vi để quan sát các vật nhỏ, người ta điều chỉnh theo cách thay đổi khoảng cách giữa vật và vật kính bằng cách đưa toàn bộ ống kính lên hay xuống sao cho nhìn thấy ảnh của vật to và rõ nhất.

Số bội giác của kính hiển vi khi ngắm chừng ở vô cực: \({G_\infty } = \left| {{k_1}} \right|{G_2} = \frac{{\delta Đ}}{{{f_1}{f_2}}}\)

A, B, D - đúng

C - sai vì: khoảng cách giữa vật kính và thị kính được giữ không đổi

A - sai vì tiêu bản phải nằm ngoài khoảng O₁F₁ và gần F₁

B, C, D - đúng

A sai vì:

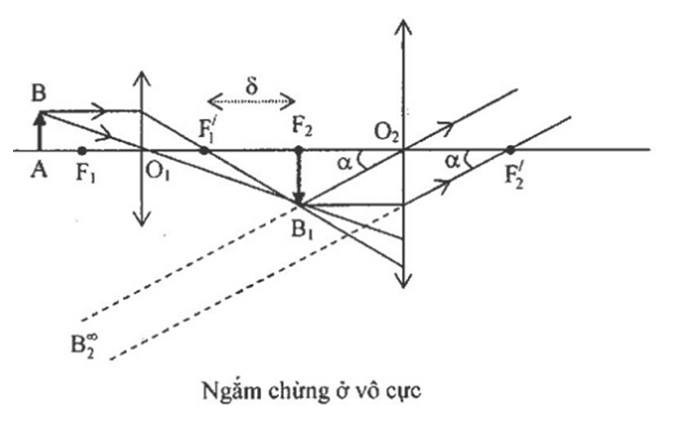
B, C, D - đúng

+ Theo bài ra: \({f_1} = 5mm = 0,5cm;{\rm{ }}{f_2} = 20mm = 2cm\)

+ Theo công thức thấu kính, vị trí ảnh qua vật kính là: \(d' = \frac{{d{f_1}}}{{d - {f_1}}} = 13cm\)

+ Theo đề bài, ta có: \({k_1} = 30;{\rm{ }}{f_2} = 2cm\) và Đ = 30 cm

+ Số bội giác của kính khi ngắm chừng ở vô cực là: \({G_\infty } = {k_1}\frac{Đ}{{{f_2}}} = 30.\frac{{30}}{2} = 450\)

+ Theo đề bài, ta có:

\({f_1} = 0,5cm;{f_2} = 2cm;{O_1}{O_2} = 12,5cm\)

\( \to \delta  = {O_1}{O_2} - \left( {{f_1} + {f_2}} \right) = 12,5 - \left( {0,5 + 2} \right) = 10cm\)

+ Số bội giác của kính khi ngắm chừng ở vô cực là: \({G_\infty } = \frac{{\delta Đ}}{{{f_1}{f_2}}} = \frac{{10.25}}{{0,5.2}} = 250\)

Theo bài ra: \({f_1} = 4mm;{\rm{ }}{f_1} = 20mm;{\rm{ }}\delta  = 156mm\) và Đ =25 cm

Khi ngắm chừng ở vô cực thì ảnh của vật qua vật kính tại tiêu diện của thị kính

\(d{'_1} = \delta  + {f_1} = 16cm\)

\( \to {d_1} = \frac{{d{'_1}{f_1}}}{{d{'_1} - {f_1}}} = 4,102256mm\)

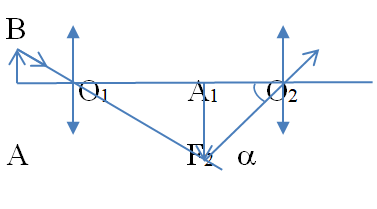
- Khi ngắm chừng vô cực:

+ \({A_1} \equiv {F_2}\)

+ góc trông ảnh: \(\alpha  = tan\alpha  = \frac{{{A_1}{B_1}}}{{{f_2}}} = \varepsilon \)    (1)

+ Độ lớn số phóng đại ảnh qua vật kính:

\(\left| {{k_1}} \right| = \frac{{{A_1}{B_1}}}{{AB}} = \frac{\delta }{{{f_1}}}\)       (2)

- Từ (1) và (2) suy ra: \(AB = \varepsilon \frac{{{f_2}{f_1}}}{\delta } = \varepsilon \frac{{{f_2}{f_1}}}{{\left( {{O_1}{O_2} - {f_1} - {f_2}} \right)}}\)

Thay số, được: \(AB = 7,{14286.10^{ - 7}}m = 0,7143\mu m\)