Ôn tập chương 1: Điện tích - Điện trường

Cọ xát thanh ebônit vào miếng dạ, thanh ebônit tích điện âm vì electron chuyển từ dạ sang thanh ebônit

Ta có:

+ Điện tích của mỗi hạt bụi:  ${q_1} = {q_2} = {8.10^8}.\left( { - {{1,6.10}^{ - 19}}} \right) =  - {1,28.10^{ - 10}}C$

+ Lực đẩy tĩnh điện giữa hai hạt là: 

$F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}} = {9.10^9}\frac{{\left| {\left( { - {{1,28.10}^{ - 10}}} \right).\left( { - {{1,28.10}^{ - 10}}} \right)} \right|}}{{{{1.0,02}^2}}} \approx {3,69.10^{ - 7}}N$

Ta có lực tương tác tĩnh điện: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{\varepsilon {r^2}}}\)

Nhận thấy \(F \sim \frac{1}{{{r^2}}}\) => Khi tăng khoảng cách giữa hai điện tích điểm lên \(3\)  lần thì lực tương tác tĩnh điện giữa chúng sẽ giảm \(9\) lần

Độ lớn điện tích trên tấm dạ chính bằng độ lớn điện tích mà thanh bônít thu được và điện tích trên tấm dạ sẽ trái dấu với điện tích của thanh bônít

=> Tấm dạ sẽ có điện tích là: \({3.10^8}C\)

+Ta có: \(Q = C.{\rm{ }}U \to U = \dfrac{{\rm{Q}}}{{\rm{C}}}\)

+ Mà ${C_1} = \dfrac{{\varepsilon {\rm{}}{\rm{.S}}}}{{9{\rm{}}{{.10}^9}.{\rm{4\pi }}.{\rm{d}}}}$

Sau đó khoảng cách giảm một nửa

$ \to {C_2} = \dfrac{{\varepsilon {\rm{}}.{\rm{S}}}}{{9{\rm{}}.{\rm{}}{{10}^9}.{\rm{4\pi }}.{\rm{}}\dfrac{{\rm{d}}}{2}}} = \dfrac{{2.{\rm{}}\varepsilon .{\rm{S}}}}{{9{\rm{}}.{\rm{}}{{10}^9}.{\rm{4\pi }}.{\rm{d}}}}$

$ \to {{\rm{C}}_2} = {\rm{}}2{{\rm{C}}_1}$

\(\begin{array}{l} \to \left\{ \begin{array}{l}{U_1} = \dfrac{Q}{{{C_1}}}\\{U_2} = \dfrac{Q}{{{C_2}}}\end{array} \right. \to \dfrac{{{U_1}}}{{{U_2}}} = \dfrac{{\dfrac{Q}{{{C_1}}}}}{{\dfrac{Q}{{{C_2}}}}} = \dfrac{{{C_2}}}{{{C_1}}} = 2\\ \to {U_2} = \dfrac{{{U_1}}}{2} = \dfrac{{300}}{2} = 150V\end{array}\)

Ta có, biểu thức của định luật Cu-lông: \(F = k\frac{{\left| {{q_1}{q_2}} \right|}}{{{r^2}}}\)

=> Lực tương tác (F) giữa hai điện tích điểm trong không khí tỉ lệ nghịch với bình phương khoảng cách giữa hai điện tích.

Ta có, cường độ điện trường: \(\overrightarrow E  = \dfrac{{\overrightarrow F }}{q} \to \overrightarrow F  = q\overrightarrow E \)

Do \(Q{\rm{ }} = {\rm{ }}CU\) mà theo đề bài \(Q\) không đổi

Do đó khi nhúng vào chất lỏng ta có:

\(\begin{array}{l}CU = C'U'\\ \leftrightarrow C.500 = C'.250\\ \to C' = \dfrac{{500}}{{250}}C = 2C = {2.2.10^{ - 3}} = {4.10^{ - 3}}\mu C\end{array}\)

Mặt khác, ta có:

\(\left\{ \begin{array}{l}C = \dfrac{S}{{{{9.10}^9}.4\pi d}}\\C' = \dfrac{{\varepsilon S}}{{{{9.10}^9}.4\pi d}}\end{array} \right. \to \dfrac{{C'}}{C} = \varepsilon \)

Ta suy ra: \(\varepsilon  = 2\)

Ta có, cường độ điện trường E:

 \(E = \frac{F}{{\left| q \right|}} = \frac{{{{3.10}^{ - 3}}}}{{{{2.10}^{ - 7}}}} = {1,5.10^4}V/m = {1,5.10^6}V/cm\)

Điện dung của bộ bốn tụ ghép nối tiếp với nhau là:

\(\begin{array}{l}\frac{1}{{{C_b}}} = \frac{1}{C} + \frac{1}{C} + \frac{1}{C} + \frac{1}{C} = \frac{4}{C}\\ \to {C_b} = \frac{C}{4}\end{array}\)

Điện dung của bộ bốn tụ ghép song song với nhau là: \({C_b} = C + C + C + C = 4C\)

- Gọi cường độ điện trường do \({q_1}\) gây ra là $E_1$; do $q_2$ gây ra là $E_2$

- Theo nguyên lí chồng chất điện trường:\(\overrightarrow E  = \overrightarrow {{E_1}}  + \overrightarrow {{E_2}} \)

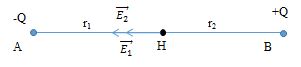
Vì \({E_1},{\rm{ }}{E_2}\) là 2 véc tơ cùng phương, cùng chiều nên: \(E{\rm{ }} = {\rm{ }}{E_1} + {\rm{ }}{E_2}\)

Ta có, cường độ điện trường:   \(E = k\dfrac{{\left| Q \right|}}{{\varepsilon .{r^2}}}\)  

Thay \({q_1} = {3.10^{ - 10}}C,{\rm{ }}{q_2} =  - {3.10^{ - 10}}C,{\rm{ }}{r_1} = {\rm{ }}{r_2} = 1cm{\rm{ }},\varepsilon  = 2\)

Ta có:  

\( \to E = 2.{E_1} = 27.{\rm{ }}{10^3}V/m\)

Các lực tác dụng lên quả cầu gồm: lực điện \(\overrightarrow F \) , trọng lực \(\overrightarrow P \)hướng xuống và lực căng dây \(\overrightarrow T \).

Khi quả cầu cân bằng: \(\overrightarrow T  + \overrightarrow P  + \overrightarrow F  = 0 \to \overrightarrow T  + \overrightarrow {P'}  = 0\)

=> $P'$ có phương sợi dây $P'$ tạo với $P$ một góc \(\alpha {\rm{ }} = {\rm{ }}{30^0}\)

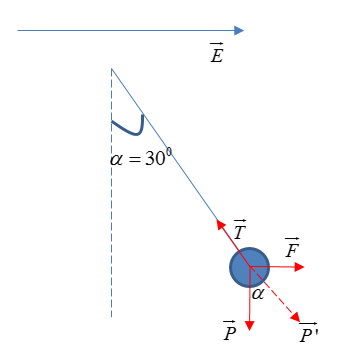
Từ hình ta có: \(\tan \alpha  = \dfrac{F}{P} = \dfrac{{\left| q \right|E}}{{mg}} = \tan {30^0} \to \left| q \right| = \dfrac{{mg\tan {{30}^0}}}{E} = \dfrac{{\sqrt 3 {{.10}^{ - 3}}.9,8.\tan {{30}^0}}}{{10000}} = {9,8.10^{ - 7}}C\)

+ Các lực tác dụng lên quả cầu \(\overrightarrow P ,\overrightarrow F ,\overrightarrow T \):

+ Quả cầu cân bằng => \(\overrightarrow P  + \overrightarrow F  + \overrightarrow T  = \overrightarrow 0 \)

+ Ta có: \(F = P\tan \alpha  = {q_0}.E = {q_0}.\dfrac{U}{d}\)

\( \Rightarrow {q_0} = \dfrac{{mgd\tan \alpha }}{U} = \dfrac{{{{0,1.10}^{ - 3}}.0,01.10.\tan 10^\circ }}{{1000}} = {1,76.10^{ - 9}}C\)

Theo bài ra ta có: \(Q{\rm{ }} = {\rm{ }}CU{\rm{ }} = {\rm{ }}24.{\rm{ }}{10^{ - 9}}.{\rm{ }}450{\rm{ }} = 1,08.{\rm{ }}{10^{ - 5}}C\)

Mà

\(\begin{array}{l}Q = n\left| e \right|\\ \to n = \frac{Q}{{\left| e \right|}} = \frac{{{{1,08.10}^{ - 5}}}}{{{{1.6.10}^{ - 19}}}} = {6,75.10^{13}}\end{array}\)

Ta có: \(U{\rm{ }} = {\rm{ }}E.{\rm{ }}d{\rm{ }} = {\rm{ }}3.{\rm{ }}{10^5}.{\rm{ }}2.{\rm{ }}{10^{ - 3}} = {\rm{ }}600V\)

=> Điện tích của tụ là \(Q{\rm{ }} = {\rm{ }}CU{\rm{ }} = {\rm{ }}600.{\rm{ }}5.{\rm{ }}{10^{ - 9}} = {\rm{ }}3.{\rm{ }}{10^{ - 6}}C\)

Ta có: \(Q{\rm{ }} = {\rm{ }}CU{\rm{ }} = {\rm{ }}200.{\rm{ }}{10^{ - 12}}.{\rm{ }}40{\rm{ }} = {\rm{ }}8.{\rm{ }}{10^{ - 9}}C\)

Lại có: \(E = \dfrac{U}{d} = \dfrac{{40}}{{{{0,2.10}^{ - 3}}}} = {2.10^5}V/m\)

Ta có:

+ Lúc đầu năng lượng của hệ là thế năng tương tác tĩnh điện: \({{\rm{W}}_1} = k\frac{{{e^2}}}{r}\)

+ Khi nó vừa thoát ra thì có vận tốc v, lúc này nó không chịu lực hút của electron nên lúc này hệ không còn thế năng tương tác mà chỉ có động năng: \({{\rm{W}}_2} = \frac{1}{2}m{v^2}\)

Áp dụng định luật bảo toàn năng lượng, ta có:

\({{\rm{W}}_1} = {{\rm{W}}_2} \leftrightarrow k\frac{{{e^2}}}{r} = \frac{1}{2}m{v_0}^2 \to {v_0} = \sqrt {\frac{{2{{\rm{e}}^2}}k}{{m{\rm{r}}}}}  = {3,2.10^6}m/s\)

Ta có: \({A_{MN}} = {\rm{ }}q.E.\overline {M'N'} \)

vì \({A_{MN}} > {\rm{ }}0;{\rm{ }}q{\rm{ }} < {\rm{ }}0;{\rm{ }}E{\rm{ }} > {\rm{ }}0\) nên \(\overline {M'N'} < 0\) tức là e đi ngược chiều đường sức.

\(\to \overline {M'N'} = - 0,008\left( m \right)\)

Cường độ điện trường: $E = \dfrac{{{A_{MN}}}}{{q.\overline {M'N'} }} = \dfrac{{{{9,6.10}^{ - 18}}}}{{\left( { - {{1,6.10}^{ - 19}}} \right).\left( { - 0,008} \right)}} = 7500(V/m)$

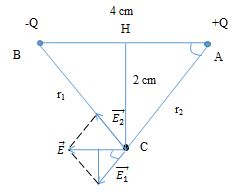
- Ta có: \({r_1} = {\rm{ }}{r_2} = r = \sqrt {A{H^2} + A{C^2}}  = 2\sqrt 2 \) cm Vì  \(\left| {{q_1}} \right|{\rm{ }} = {\rm{ }}\left| {{q_2}} \right|\)  và \({r_1} = {\rm{ }}{r_2}\) \( =  > {E_1} = {\rm{ }}{E_2}\)

- Từ hình vẽ ta có: $E = 2{E_1}c{\rm{os}}\alpha $

Với \(\cos \alpha  = \dfrac{{AH}}{{AC}} = \dfrac{2}{{2\sqrt 2 }} = \dfrac{{\sqrt 2 }}{2}\)

=> \(E = 2{E_1}\dfrac{{\sqrt 2 }}{2} = {E_1}\sqrt 2 \)

Ta có: \({E_1} = k\dfrac{{\left| {{q_2}} \right|}}{{\varepsilon .{r_1}^2}} = {9.10^9}\dfrac{{\left| {{{8.10}^{ - 8}}} \right|}}{{1.{{(2.\sqrt 2 {{.10}^{ - 2}})}^2}}} = {9.10^5}V/m\)

\( \to E = \sqrt 2 {.9.10^5} \approx {\rm{ }}12,73.{\rm{ }}{10^5}V/m\)