Một tụ điện có điện dung C, được nạp điện đến hiệu điện thế U, điện tích của tụ là Q. Công thức nào sau đây không phải là công thức xác định năng lượng của tụ điện?
Ta có: \(W = \frac{{Q.U}}{2} = \frac{{C.{U^2}}}{2} = \frac{{{Q^2}}}{{2C}}\)
Một tụ điện phẳng có điện môi không khí; khoảng cách giữa 2 bản là \(d{\rm{ }} = {\rm{ }}0,6{\rm{ }}cm\) ; diện tích một bản là \(36{\rm{ }}c{m^2}\). Mắc tụ vào nguồn điện có hiệu điện thế $U=100V$. Năng lượng điện trường trong tụ điện là:
+ Điện dung của tụ điện: \(C = \dfrac{{\varepsilon .S}}{{{{9.10}^9}.4\pi .d}} = \dfrac{{{{36.10}^{ - 4}}}}{{{{9.10}^9}.4\pi .0,006}} = \dfrac{1}{{60\pi }}(nF)\)
+ Năng lượng điện trường:\(W = \dfrac{1}{2}C{U^2} = \dfrac{1}{2}\dfrac{1}{{60\pi }}{.10^{ - 9}}{.10^4} = \dfrac{1}{{12\pi }}(\mu J)\)
Cho bộ tụ điện mắc như hình vẽ.
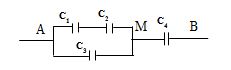
\({C_1} = 4\mu F;{C_2} = 6,5\mu F\),\({C_3} = 3,6\mu F;{C_4} = 6\mu F\). Mắc $2$ cực $AB$ vào hiệu điện thế $U{\rm{ }} = {\rm{ }}100V$. Điện dung của bộ tụ là:
Cấu tạo của mạch điện:$\left[ {\left( {{{\rm{C}}_{\rm{1}}}{\rm{ nt }}{{\rm{C}}_{\rm{2}}}} \right){\rm{//}}{{\rm{C}}_{\rm{3}}}} \right]{\rm{ nt }}{{\rm{C}}_{\rm{4}}}$
Lại có:
+Điện dung của tụ khi ghép nối tiếp:\(\dfrac{1}{{{C_{nt}}}} = \dfrac{1}{{{C_1}}} + \dfrac{1}{{{C_2}}} + ... + \dfrac{1}{{{C_n}}}\)
+ Điện dung của tụ khi ghép song song: \({C_{//}} = {\rm{ }}{C_1} + {\rm{ }}{C_2} + {\rm{ }} \ldots + {\rm{ }}{C_n}\)
Ta suy ra điện dung của bộ tụ:
${C_{12}} = \dfrac{{{C_1}{C_2}}}{{{C_1} + {C_2}}} = \dfrac{{4.6,5}}{{4 + 6,5}} = 2,48\left( {\mu F} \right)$
${C_{AM}} = {C_{12}} + {C_3} = 2,48 + 3,6 = 6,08\left( {\mu F} \right)$
${C_{AB}} = \frac{{{C_{AM}}{C_4}}}{{{C_{AM}} + {C_4}}} = \dfrac{{6,08.6}}{{6,08 + 6}} = 3,02\left( {\mu F} \right)$

