Tính khoảng cách giữa hai điểm trên Mặt Trăng, nếu góc trông hai điểm này qua kính là \(4'\). Coi khoảng cách từ Trái Đất đến Mặt Trăng là \(400000km\)?
+ Số bội giác: \({G_\infty } = \frac{\alpha }{{{\alpha _0}}} = 100 \to {\alpha _0} = \frac{\alpha }{{100}}\)
Ta có: \(\alpha = 4' = \frac{4}{{60}}\frac{\pi }{{180}} = {1,16.10^{ - 3}}\left( {ra{\rm{d}}} \right) \to {\alpha _0} = {1,16.10^{ - 5}}\left( {ra{\rm{d}}} \right)\)
+ Mặt khác, ta có:
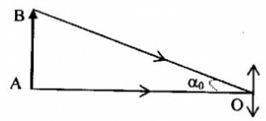
\(\begin{array}{l}\tan {\alpha _0} = \frac{{AB}}{{OA}} \approx {\alpha _0}\\ \to AB = OA.{\alpha _0} = {4.10^5}{.1,16.10^{ - 5}} = 4,65\left( {km} \right)\end{array}\)
Số bội giác của kính thiên văn khi ngắm chừng ở vô cực là:
+ Tiêu cự của vật kính: \({f_1} = \frac{1}{{0,5}} = 2m = 200cm\)
+ Số bội giác: \({G_\infty } = \frac{{{f_1}}}{{{f_2}}} = \frac{{200}}{2} = 100\)
Tìm tiêu cự của thị kính?
Ta có: Vật \({A_1}{B_1}\) đặt tại tiêu diện vật \({F_2}\) của thị kính nên ảnh \({A_2}{B_2}\) ở vô cực, ta có:
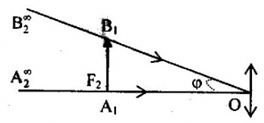
\(\begin{array}{l}\tan \varphi = \frac{{{A_1}{B_1}}}{{{f_2}}} \approx \varphi \\ \to {f_2} = \frac{{{A_1}{B_1}}}{\varphi } = \frac{{0,1}}{{0,05}} = 2cm\end{array}\)
Vật kính của một kính thiên văn học sinh gồm vật kính có tiêu cự \({f_1} = 120cm\), thị kính có tiêu cự \({f_2} = 4cm\). Một học sinh có điểm cực viễn cách mắt \(50cm\) quan sát ảnh của Mặt Trăng qua kính thiên văn nói trên sao cho mắt không điều tiết. Tính khoảng cách giữa hai kính?
+ Mắt quan sát ảnh ảo \({A_2}{B_2}\) ở trạng thái mắt không điều tiết nên \({A_2}{B_2}\) ở cực viễn của mắt tức \({d_2}' = - {O_2}{A_2} = - O{V_V} = - 50cm\)
\( \Rightarrow {A_1}{B_1}\) cách thị kính \({d_2} = {O_2}{A_1} = \dfrac{{{d_2}'{f_2}}}{{{d_2}' - {f_2}}} = \dfrac{{ - 50.4}}{{ - 50 - 4}} = 3,7cm\)
+ Khoảng cách giữa hai kính \({O_1}{O_2} = {f_1} + {d_2} = 120 + 3,7 = 123,7cm\)
Tìm tiêu cự của thị kính?
Ta có: Vật \({A_1}{B_1}\) đặt tại tiêu diện vật \({F_2}\) của thị kính nên ảnh \({A_2}{B_2}\) ở vô cực, ta có:

\(\begin{array}{l}\tan \varphi = \frac{{{A_1}{B_1}}}{{{f_2}}} \approx \varphi \\ \to {f_2} = \frac{{{A_1}{B_1}}}{\varphi } = \frac{{0,1}}{{0,05}} = 2cm\end{array}\)
Vật kính của một kính thiên văn có tiêu cự 80 cm, thị kính có tiêu cự 4 cm. Người quan sát có điểm cực cận cách mắt 20 cm, điểm cực viễn ở vô cực, đặt mắt sát thị kính để quan sát một chòm sao. Tính khoảng cách giữa vật kính và thị kính khi ngắm chừng ở cực cận?
Ta có:
+ Khi quan sát chòm sao: \({d_1} = \infty \to {d_1}' = {f_1} = 80cm\)
+ Khi ngắm chừng ở điểm cực cận:
\(\begin{array}{l}{d_2}' = - O{C_C} = - 20cm\\ \to {d_2} = \dfrac{{{d_2}'{f_2}}}{{{d_2}' - {f_2}}} = \dfrac{{ - 20.4}}{{ - 20 - 4}} = \dfrac{{10}}{3}cm\end{array}\)
+ Khoảng cách giữa vật kính và thị kính: \({O_1}{O_2} = {d_1}' + {d_2} = 80 + \dfrac{{10}}{3} = 83,33cm\)
Số bội giác của kính thiên văn khi ngắm chừng ở vô cực là:
+ Tiêu cự của vật kính: \({f_1} = \dfrac{1}{{0,4}} = 2,5m = 250cm\)
+ Số bội giác: \({G_\infty } = \dfrac{{{f_1}}}{{{f_2}}} = \dfrac{{250}}{1} = 250\)
Tìm tiêu cự của thị kính?
Ta có: Vật \({A_1}{B_1}\) đặt tại tiêu diện vật \({F_2}\) của thị kính nên ảnh \({A_2}{B_2}\) ở vô cực, ta có:
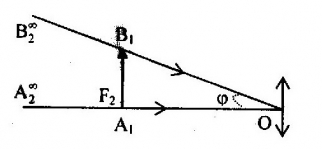
Ta có \({A_1}{B_1} = 1mm = 0,1cm\)
\(\begin{array}{l}\tan \varphi = \dfrac{{{A_1}{B_1}}}{{{f_2}}} \approx \varphi \\ \to {f_2} = \dfrac{{{A_1}{B_1}}}{\varphi } = \dfrac{{0,1}}{{0,01}} = 1cm\end{array}\)
Tìm tiêu cự của thị kính?
Ta có: Vật \({A_1}{B_1}\) đặt tại tiêu diện vật \({F_2}\) của thị kính nên ảnh \({A_2}{B_2}\) ở vô cực, ta có:

Ta có \({A_1}{B_1} = 1mm = 0,1cm\)
\(\begin{array}{l}\tan \varphi = \dfrac{{{A_1}{B_1}}}{{{f_2}}} \approx \varphi \\ \to {f_2} = \dfrac{{{A_1}{B_1}}}{\varphi } = \dfrac{{0,1}}{{0,01}} = 1cm\end{array}\)
Tính khoảng cách giữa hai điểm trên Mặt Trăng, nếu góc trông hai điểm này qua kính là \(4'\). Coi khoảng cách từ Trái Đất đến Mặt Trăng là \(400000km\)?
+ Số bội giác: \({G_\infty } = \dfrac{\alpha }{{{\alpha _0}}} = 250 \to {\alpha _0} = \dfrac{\alpha }{{250}}\)
Ta có: \(\alpha = 4' = \dfrac{4}{{60}}\dfrac{\pi }{{180}} = {1,16.10^{ - 3}}\left( {ra{\rm{d}}} \right) \Rightarrow {\alpha _0} = {4,64.10^{ - 6}}\left( {ra{\rm{d}}} \right)\)
+ Mặt khác, ta có:
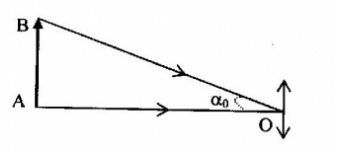
\(\begin{array}{l}\tan {\alpha _0} = \dfrac{{AB}}{{OA}} \approx {\alpha _0}\\ \to AB = OA.{\alpha _0} = {4.10^5}{.4,64.10^{ - 6}} \approx 1,86\left( {km} \right)\end{array}\)
Một kính thiên văn khúc xạ được điều chỉnh cho một nguời có mắt bình thường nhìn được rõ nét của một vật ở vô cực mà không phải điều tiết. Khi đó, khoảng cách giữa vật kính và thị kính là 62cm và số bội giác của kính là 30. Xác định tiêu cự của vật kính và thị kính.
Ta có
+ Sơ đồ tạo ảnh qua hệ thấu kính:
+ Vì quan sát Mặt Trăng ở rất xa nên
![]()
+ Ngắm chừng ở vô cực nên:
![]()
+ Khoảng cách giữa hai kính: \({O_1}{O_2} = {f_1} + {f_2} = 62cm\,\,\,\left( 1 \right)\)
+ Số bội giác của kính thiên văn khi ngắm chừng ở vô cực: \({G_\infty } = \dfrac{{{f_1}}}{{{f_2}}} = 30\,\,\,\left( 2 \right)\)
Từ (1) và (2), ta suy ra: \(\left\{ \begin{array}{l}{f_1} = 60cm\\{f_2} = 2cm\end{array} \right.\)
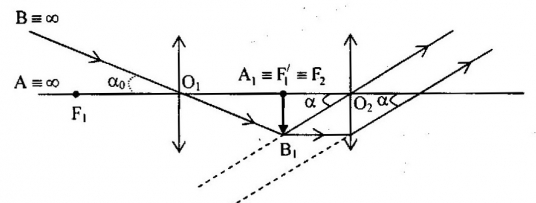
Một kính thiên văn khúc xạ được điều chỉnh cho một nguời có mắt bình thường nhìn được rõ nét của một vật ở vô cực mà không phải điều tiết. Khi đó, khoảng cách giữa vật kính và thị kính là 84cm và số bội giác của kính là 20. Vật quan sát Mặt Trăng có góc trông \({\alpha _0} = \dfrac{1}{{100}}ra{\rm{d}}\). Đường kính của mặt trăng cho bởi vật kính là:
Ta có
+ Sơ đồ tạo ảnh qua hệ thấu kính:

+ Vì quan sát Mặt Trăng ở rất xa nên
![]()
+ Ngắm chừng ở vô cực nên:
![]()
+ Khoảng cách giữa hai kính: \({O_1}{O_2} = {f_1} + {f_2} = 84cm\,\,\,\left( 1 \right)\)
+ Số bội giác của kính thiên văn khi ngắm chừng ở vô cực: \({G_\infty } = \dfrac{{{f_1}}}{{{f_2}}} = 20\,\,\,\left( 2 \right)\)
Từ (1) và (2), ta suy ra: \(\left\{ \begin{array}{l}{f_1} = 80cm\\{f_2} = 4cm\end{array} \right.\)

Ta có:
\(\begin{array}{l}\tan {\alpha _0} = \dfrac{{{A_1}{B_1}}}{{{f_1}}}\\ \to {A_1}{B_1} = {f_1}\tan {\alpha _0} \approx {f_1}.{\alpha _0} = \dfrac{{80}}{{100}} = 0,8\left( {cm} \right)\end{array}\)
Tìm tiêu cự của thị kính?
Ta có: Vật \({A_1}{B_1}\) đặt tại tiêu diện vật \({F_2}\) của thị kính nên ảnh \({A_2}{B_2}\) ở vô cực, ta có:

\(\begin{array}{l}\tan \varphi = \frac{{{A_1}{B_1}}}{{{f_2}}} \approx \varphi \\ \to {f_2} = \frac{{{A_1}{B_1}}}{\varphi } = \frac{{0,1}}{{0,05}} = 2cm\end{array}\)
Một kính thiên văn khi được điều chỉnh để ngắm chừng ở vô cực thì khoảng cách giữa vật kính và thị kính là 100 cm, độ bội giác của kính là 24. Tiêu cự của vật kính và thị kính bằng
Độ dài quang học của kính thiên văn: \(\delta = {f_1} + {f_2}\)
Độ bội giác khi ngắm chừng ở vô cực: \({G_\infty } = \frac{{{f_1}}}{{{f_2}}}\)
Vậy ta có :
\(\left\{ \begin{array}{l}
{f_1} + {f_2} = 100\\
\frac{{{f_1}}}{{{f_2}}} = 24
\end{array} \right. \Rightarrow \left\{ \begin{array}{l}
{f_1} = 96cm\\
{f_2} = 4cm
\end{array} \right.\)
Một người mắt bình thường điều chỉnh kính thiên văn để quan sát ảnh của một ngôi sao ở xa mà không cần điều tiết. Tiêu cự của vật kính và thị kính của kính thiên văn lần lượt là 1m và 5cm. Độ bội giác của ảnh quan sát qua kính là
Để mắt quan sát mà không phải điều tiết thì ngắm chừng ở vô cực
Độ bội giác của kính là: \(G=\frac{{{f}_{1}}}{{{f}_{2}}}=\frac{100}{5}=20\)
Một kính thiên văn mà vật kính có tiêu cự f1 = 2m. Người quan sát mắt không có tật. Số bội giác của kính khi người đó ngắm chừng ở vô cực là 50. Thị kính có tiêu cự bằng
Cách giải:
Ta có: \({G_\infty } = \frac{{{f_1}}}{{{f_2}}} \Rightarrow {f_2} = \frac{{{f_1}}}{{{G_\infty }}} = \frac{2}{{50}} = 4cm\)
Đề thi thử THPT QG trường Lý Thường Kiệt - 2021
Vật kính của một kính thiên văn có tiêu cự \({f_1} = 1,2m\). Hỏi tiêu cự \({f_2}\) của thị kính bằng bao nhiêu để khi ngắm chừng ở vô cực, độ bội giác của kính bằng 60.
Từ công thức tính số bội giác trong trường hợp ngắm chừng ở vô cực ta có:
\({G_\infty } = \dfrac{{{f_1}}}{{{f_2}}} \Rightarrow {f_2} = \dfrac{{{f_1}}}{{{G_\infty }}} = \dfrac{{1,2}}{{60}} = 0,02m = 2cm\)
Ý kiến nào sau đây đúng về kính thiên văn?
A - sai vì thị kính là kính lúp để quan sát ảnh tạo bởi vật kính và vật kính là thấu kính hội tụ có tiêu cự lớn (có thể tới hàng chục mét)
B – sai vì vật kính có tiêu cự rất dài, thị kính là kính lúp để quan sát ảnh tạo bởi vật kính.
C – sai vì Khoảng cách giữa hai kính thay đổi được
D - đúng
Khi ngắm chừng vô cực một vật ở xa bằng kính thiên văn, đáp án nào sau đây đúng?
A, B - sai vì: khi ngắm chừng ở vô cực thì khoảng cách hai kính là \({O_1}{O_2} = {f_1} + {f_2}\)
C – sai vì: Số bội giác vô cực của kính là \({G_\infty } = \dfrac{{{f_1}}}{{{f_2}}}\)
D - đúng
Một kính thiên văn, vật kính có tiêu cự \({f_1} = 1m\), thị kính có tiêu cự \(5{\rm{ }}cm\). Người quan sát mắt bình thường, ngắm chừng không điều tiết. Số bội giác vô cực của kính thiên văn này là:
Ta có,
+ Tiêu cự của vật kính: \({f_1} = 1m\)
+ Tiêu cự của thị kính: \({f_2} = 5cm\)
=> Số bội giác của kính thiên văn: \({G_\infty } = \dfrac{{{f_1}}}{{{f_2}}} = \dfrac{1}{{0,05}} = 20\)

