Câu hỏi:
2 năm trước
Tính khoảng cách giữa hai điểm trên Mặt Trăng, nếu góc trông hai điểm này qua kính là \(4'\). Coi khoảng cách từ Trái Đất đến Mặt Trăng là \(400000km\)?
Trả lời bởi giáo viên
Đáp án đúng: d
+ Số bội giác: \({G_\infty } = \dfrac{\alpha }{{{\alpha _0}}} = 250 \to {\alpha _0} = \dfrac{\alpha }{{250}}\)
Ta có: \(\alpha = 4' = \dfrac{4}{{60}}\dfrac{\pi }{{180}} = {1,16.10^{ - 3}}\left( {ra{\rm{d}}} \right) \Rightarrow {\alpha _0} = {4,64.10^{ - 6}}\left( {ra{\rm{d}}} \right)\)
+ Mặt khác, ta có:
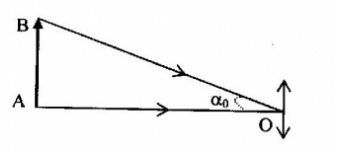
\(\begin{array}{l}\tan {\alpha _0} = \dfrac{{AB}}{{OA}} \approx {\alpha _0}\\ \to AB = OA.{\alpha _0} = {4.10^5}{.4,64.10^{ - 6}} \approx 1,86\left( {km} \right)\end{array}\)
Hướng dẫn giải:
+ Áp dụng biểu thức tính số bội giác của kính thiên văn khi ngắm chừng ở vô cực: \({G_\infty } = \dfrac{{{f_1}}}{{{f_2}}} = \dfrac{\alpha }{{{\alpha _0}}}\) (đã tính được ở câu trên)
+ Sử dụng công thức tính góc trông \(\tan {\alpha _0} = \dfrac{{AB}}{{OA}}\)
