Một thấu kính hội tụ có tiêu cự 30 cm, Vật sáng AB đặt vuông góc với trục chính của thấu kính. Ảnh của vật tạo bởi thấu kính là ảnh ảo và cách vật 40 cm. Khoảng cách từ AB đến thấu kính có giá trị gần nhất với giá trị nào sau đây ?
Vật thật nên d > 0; ảnh ảo nên d’ < 0.
Áp dụng công thức thấu kính ta có:
\(\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f} = \frac{1}{{30}}\,\,\,\left( 1 \right)\)
Khoảng cách giữa ảnh và vật là:
\(L = \left| {d + d'} \right| = 40cm \Rightarrow \left[ \begin{array}{l}
d + d' = 40\\
d + d' = - 40
\end{array} \right.{\mkern 1mu} {\mkern 1mu} \left( 2 \right)\)
Từ (1) và (2) ta có hệ phương trình:
\(\frac{{d.d'}}{{d + d'}} = f \Rightarrow \left[ \begin{array}{l}
\frac{{d.d'}}{{40}} = 30\,\,\left( {vo\,nghiem} \right)\\
\frac{{d.d'}}{{ - 40}} = 30
\end{array} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{l}}
{d = 20\,\,cm}\\
{d' = - 60\,\,cm}
\end{array}} \right.\)
Vậy khoảng cách từ vật đến TK gần nhất với 21 cm.
Vật sáng \(AB\) đặt trước một thấu kính hội tụ cho ảnh rõ nét trên màn cách vật \(90\,\,cm\). Biết ảnh cao gấp hai lần vật. Tiêu cự của thấu kính là
Ảnh thật cao gấp 2 lần vật, ta có:
\(\left\{ \begin{array}{l}\dfrac{{d'}}{d} = 2\\d + d' = 90\end{array} \right. \Rightarrow \left\{ \begin{array}{l}d = 30\,\,\left( {cm} \right)\\d' = 60\,\,\left( {cm} \right)\end{array} \right.\)
Áp dụng công thức thấu kính, ta có:
\(\dfrac{1}{d} + \dfrac{1}{{d'}} = \dfrac{1}{f} \Rightarrow \dfrac{1}{{30}} + \dfrac{1}{{60}} = \dfrac{1}{f} \Rightarrow f = 20\,\,\left( {cm} \right)\)
Đặt vật sáng phẳng, nhỏ trước thấu kính phân kì tiêu cự \(f = - 10\,\,cm\), cách thấu kính \(d = 20\,\,cm\). Ảnh thu được
Ta có công thức thấu kính:
\(\dfrac{1}{d} + \dfrac{1}{{d'}} = \dfrac{1}{f} \Rightarrow \dfrac{1}{{20}} + \dfrac{1}{{d'}} = \dfrac{1}{{ - 10}} \Rightarrow d' = - \dfrac{{20}}{3}\,\,\left( {cm} \right)\)
Độ phóng đại của ảnh là:
\(\dfrac{{A'B'}}{{AB}} = \left| {\dfrac{{d'}}{d}} \right| = \left| {\dfrac{{\dfrac{{ - 20}}{3}}}{{20}}} \right| = \dfrac{1}{3}\) → ảnh nhỏ hơn vật 3 lần
Vật sáng AB đặt vuông góc với trục chính của một thấu kính hội tụ có tiêu cự 25 cm. Khoảng cách giữa AB và ảnh thật của nó tạo bởi thấu kính là L. Giá trị nhỏ nhất của L gần nhất với giá trị nào sau đây?
Ta có:
\(\left\{ \begin{array}{l}
\frac{1}{d} + \frac{1}{{d'}} = \frac{1}{f}\\
L = d + d'
\end{array} \right.\)
\(\begin{array}{l}
\frac{1}{d} + \frac{1}{{L - d}} = \frac{1}{f} \Leftrightarrow \left( {L - d} \right).f + fd = d.\left( {L - d} \right)\\
\Leftrightarrow {d^2} - Ld + Lf = 0
\end{array}\)
Để phương trình trên có nghiệm thì:
\(\Delta \ge 0 \Leftrightarrow {L^2} - 4Lf \ge 0 \Leftrightarrow L \ge 4f\)
Vậy giá trị nhỏ nhất của:
\({L_{\min }} = 4f = 4.25 = 100cm\)
Giá trị gần nhất là 98 cm
Ở hình bên, xy là trục chính của thấu kính L, S là một điểm sáng trước thấu kính, S’ là ảnh của S cho bởi thấu kính. Kết luận nào sau đây đúng ?
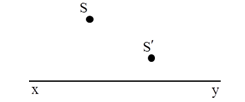
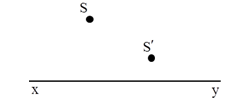
S và S’ cùng phía so với trục chính do đó S’ là ảnh ảo.
S’ gần trục chính hơn nên thấu kính đã cho là TKPK.
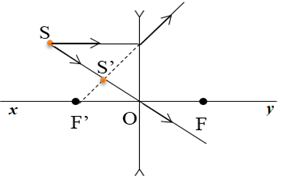
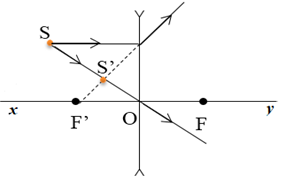
→ L là thấu kính phân kì đặt tại giao điểm của đường thẳng SS’ với xy.
Cho một thấu kính L có độ tụ D = 5điôp. Xác định vị trí, tính chất và độ lớn của ảnh tạo bởi một vật AB cao 2cm, vuông góc với trục chính. Cho biết: AB là vật thật, cách L là 10cm:
Tiêu cự của thấu kính: \(f = \dfrac{1}{D} = \dfrac{1}{5} = 0,2m = 20cm\)
Ta có: \(AB = 2cm;{\rm{ }}d = 10cm\)
Áp dụng công thức thấu kính xác định vị trí ảnh ta có :
\(\dfrac{1}{d} + \dfrac{1}{{d'}} = \dfrac{1}{f} \Rightarrow d' = \dfrac{{df}}{{d - f}} = \dfrac{{10.20}}{{10 - 20}} = - 20cm < 0\)
→ Ảnh A'B' là ảnh ảo hiện ra trước thấu kính và cách thấu kính 20cm.
Số phóng đại ảnh: \(k = \dfrac{{\overline {A'B'} }}{{\overline {AB} }} = - \dfrac{{d'}}{d} = - \dfrac{{\left( { - 20} \right)}}{{10}} = 2\)
Độ lớn của ảnh: \(A'B' = \left| k \right|.AB = 2.2 = 4cm\)
Hình vẽ:
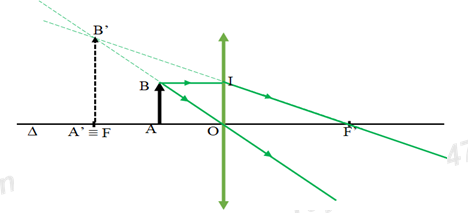
Cho một thấu kính L có độ tụ D = 5điôp. Xác định vị trí, tính chất và độ lớn của ảnh tạo bởi một vật AB cao 2cm, vuông góc với trục chính. Cho biết: AB là vật thật, cách L là 30cm.
Tiêu cự của thấu kính: \(f = \dfrac{1}{D} = \dfrac{1}{5} = 0,2m = 20cm\)
Ta có: \(AB = 2cm;{\rm{ }}d = 30cm\)
Áp dụng công thức thấu kính xác định vị trí ảnh ta có :
\(\dfrac{1}{d} + \dfrac{1}{{d'}} = \dfrac{1}{f} \Rightarrow d' = \dfrac{{df}}{{d - f}} = \dfrac{{30.20}}{{30 - 20}} = 60cm > 0\)
→ Ảnh A'B' là ảnh thật hiện ra sau thấu kính và cách thấu kính 60cm.
Số phóng đại ảnh: \(k = \dfrac{{\overline {A'B'} }}{{\overline {AB} }} = - \dfrac{{d'}}{d} = - \dfrac{{60}}{{30}} = - 2\)
Độ lớn của ảnh: \(A'B' = \left| k \right|.AB = 2.2 = 4cm\)
Hình vẽ:
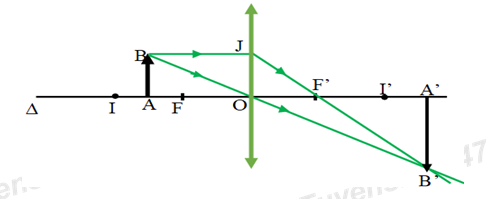
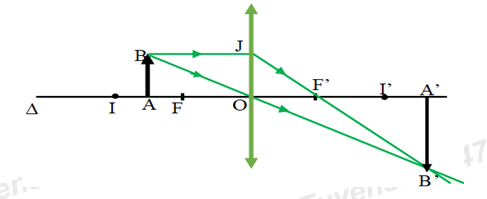
Vật sáng AB đặt vuông góc với trục chính của một thấu kính phẳng lồi bằng thủy tinh chiết suất \(n = 1,5\) bán kính mặt lồi bằng \(10cm\) , cho ảnh rõ nét trên màn đặt cách vật một khoảng L. Khoảng cách ngắn nhất của L là:
Hướng dẫn giải:
Ta có:
+ Tiêu cự của thấu kính:
\(\begin{array}{l}\frac{1}{f} = \left( {n - 1} \right)\left( {\frac{1}{{{R_1}}} + \frac{1}{{{R_2}}}} \right)\\ = \left( {1,5 - 1} \right)\left( {\frac{1}{{10}} + \frac{1}{\infty }} \right) = \frac{1}{{20}}\\ \to f = 20cm\end{array}\)
+ Vì ảnh hứng trên màn là ảnh thật nên \(d' > 0 \to L = d + d'\) (1)
+ \(\frac{1}{f} = \frac{1}{d} + \frac{1}{{d'}} \to d = \frac{{d'f}}{{d' - f}}\) (2)
Thế (2) vào (1), ta được: \(L = \frac{{d'f}}{{d' - f}} + d'\)
\( \leftrightarrow L\left( {d' - f} \right) = d{'^2} \leftrightarrow d{'^2} - L{\rm{d}}' + fL = 0\) (3)
Vì trên màn thu được ảnh rõ nét nên phương trình (3) phải có nghiệm hay \(\Delta \ge 0\)
\(\begin{array}{l}\Delta = {b^2} - 4{\rm{a}}c = {L^2} - 4fL \ge 0\\ \to L \ge 4f \to {L_{\min }} = 4f = 4.20 = 80cm\end{array}\)
Một thấu kính hội tụ có tiêu cự \(30 cm\). Vật sáng AB đặt vuông góc với trục chính của thấu kính. Ảnh của vật tạo bởi thấu kính là ảnh ảo và cách vật \(40 cm\). Khoảng cách từ AB đến thấu kính có giá trị gần nhất với giá trị nào sau đây?
Ta có, vật AB qua thấu kính hội tụ cho ảnh ảo
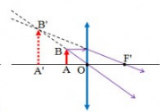
Do ảnh thu được là ảnh ảo, nên ta có:
\(\dfrac{1}{f} = \dfrac{1}{d} - \dfrac{1}{{d'}}\) (1)
Theo đầu bài, ta có: \(\left\{ \begin{array}{l}f = 30cm\\d' - d = 40cm\end{array} \right.\)
Thay vào (1), ta được:
\(\begin{array}{l}\dfrac{1}{{30}} = \dfrac{1}{d} - \dfrac{1}{{d + 40}}\\ \leftrightarrow d\left( {d + 40} \right) = 30\left( {d + 40} \right) - 30d\\ \leftrightarrow {d^2} + 40d - 1200 = 0\\ \to \left[ \begin{array}{l}d = 20cm\\d = - 60cm\end{array} \right.\end{array}\)
Hãy cho biết A’B’ là ảnh gì?
Ta có: AB và A’B’ cùng chiều => ảnh và vật trái tính chất
Vì AB là vật thật => ảnh A’B’ là ảnh ảo
Hãy cho biết S’ là ảnh gì và thấu kính thuộc loại nào?
Ta có:
+ Vì S’ và S ở khác phía trục chính nên S và S’ cùng tính chất => S’ là ảnh thật.
+ Vật thật cho ảnh thật => thấu kính là thấu kính hội tụ
Một thấu kính hội tụ có tiêu cự \(30 cm\). Vật sáng AB đặt vuông góc với trục chính của thấu kính. Ảnh của vật tạo bởi thấu kính ngược chiều với vật và cao gấp ba lần vật. Vật AB cách thấu kính
Do ảnh ngược chiều cao gấp 3 lần vật \(k=-3=-\dfrac{d'}{d}\)
\( \to d'=3d\)
Lại có: \(\dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{d'}\)
\(\to \dfrac{1}{f}=\dfrac{1}{d}+\dfrac{1}{3d}=\dfrac{4}{3d}\)
\( \to d= \dfrac{4}{3}f=\dfrac{4}{3}.30 \to d = 40cm\)
Vật AB đặt vuông góc với trục chính của một thấu kính tại A cho ảnh A’B’. Biết A’B’ cao gấp \(3\) lần AB và cách AB một khoảng \(120cm\). Thấu kính này là thấu kính
+ Nếu ảnh là ảnh thật: k = -3 => d’ = 3d
Mà d + d’ = 120cm => d = 30cm; d’ = 90cm
ÁP dụng công thức thấu kính : \(\dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}} = \dfrac{1}{{30}} + \dfrac{1}{{90}} \Rightarrow f = 22,5cm\)
+ Nếu ảnh là ảnh ảo : k = 3 => d’ = -3d
Khoảng cách từ vật đến ảnh : -d’ – d = 120cm => d = -30cm loại vì vật là vật thật thì d > 0
Vậy thấu kính hội tụ có tiêu cự 22,5cm
thấu kính thuộc loại nào và vật được đặt trước hay sau thấu kính?
+ Ta có, ảnh A’B’ lớn hơn vật AB nên thấu kính là thấu kính hội tụ
+ Xác định vị trí vật:
- Vì điểm vật, điểm ảnh, quang tâm thẳng hàng => nối BB’ thì cắt trục chính xy tại $O$.
- Qua $O$ dựng thấu kính hội tụ.
- Từ B kẻ tia tới BI // xy thì tia ló qua I có đường kéo dài qua B’ cắt trục chính tại F’. Lấy F đối xứng với F’ qua O.
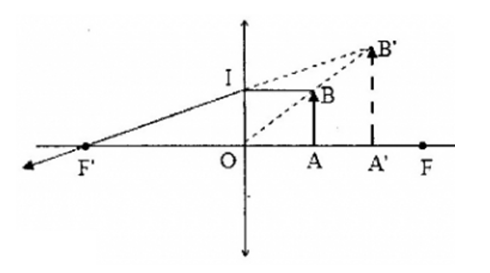
Hãy cho biết A’B’ là ảnh gì?
Ta có: AB và A’B’ cùng chiều => ảnh và vật trái tính chất
Vì AB là vật thật => ảnh A’B’ là ảnh ảo
Hãy cho biết A’B’ là ảnh gì?
Ta có: AB và A’B’ cùng chiều => ảnh và vật trái tính chất
Vì AB là vật thật => ảnh A’B’ là ảnh ảo
Gọi d là khoảng cách từ S đến thấu kính, d nằm trong khoảng nào?
+ Vì điểm vật, điểm ảnh và quang tâm O thẳng hàng nên nối SS’ cắt trục chính tại điểm O là quang tâm.
+ Qua O dựng thấu kính hội tụ vuông góc với trục chính.
+ Kẻ tia SI // xy thì tia ló qua IS’, cắt xy tại F’. Lấy F đối xứng với F’ qua O.
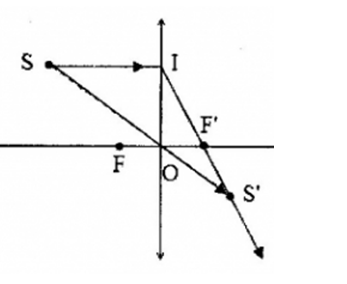
=> điểm S nằm ngoài tiêu cực, d > OF
Hãy cho biết S’ là ảnh gì và thấu kính thuộc loại nào?
Ta có:
+ Vì S’ và S ở khác phía trục chính nên S và S’ cùng tính chất => S’ là ảnh thật.
+ Vật thật cho ảnh thật => thấu kính là thấu kính hội tụ
Hãy cho biết S’ là ảnh gì và thấu kính thuộc loại nào?
Ta có:
+ Vì S’ và S ở khác phía trục chính nên S và S’ cùng tính chất => S’ là ảnh thật.
+ Vật thật cho ảnh thật => thấu kính là thấu kính hội tụ
Vật sáng AB đặt vuông góc với trục chính của một thấu kính hội tụ có tiêu cự \(f = 12 cm\). Để ảnh của vật có độ cao vằng vật thì phải đặt vật cách thấu kính 1 khoảng bằng
Để ảnh cao bằng vật ta có \(\left| k \right| = \dfrac{{d'}}{d} = \dfrac{{A'B'}}{{AB}} = 1 = > d' = d\)
Áp dụng công thức thấu kính ta có \(\dfrac{1}{d} + \dfrac{1}{{d'}} = \dfrac{1}{f} = > \dfrac{1}{d} + \dfrac{1}{d} = \dfrac{1}{f} = > \dfrac{2}{d} = \dfrac{1}{f} = d = 2f = 24cm\)

