Khúc xạ ánh sáng

Hiện tượng khúc xạ ánh sáng là hiện tượng ánh sáng bị gãy khúc khi truyền xiên góc qua mặt phân cách giữa hai môi trường trong suốt

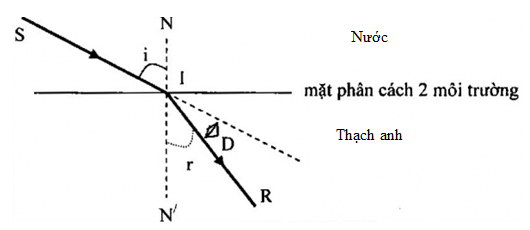
Ta có:

\(\begin{array}{l}{n_1}\sin i = {n_2}{\mathop{\rm s}\nolimits} {\rm{inr}}\\ \Rightarrow {\mathop{\rm s}\nolimits} {\rm{inr}} = \dfrac{{{n_1}\sin i}}{{{n_2}}} = \dfrac{{\dfrac{4}{3}.\sin {{30}^0}}}{{1,55}} = 0,43\\ \Rightarrow r = 25,{5^0}\end{array}\)

Khi ánh sáng truyền từ môi trường có chiết suất \({n_1}\) sang môi trường có chiết suất \({n_2}\) thì công thức của định luật khúc xạ ánh sáng là: \({n_1}\sin i = {n_2}\sin r\)

Chiết suất tỉ đối của hai môi trường: \({n_{21}} = \dfrac{{{n_2}}}{{{n_1}}} = \dfrac{{\sin i}}{{\sin r}}\) → B sai

→ chiết suất tỉ đối phụ thuộc vào môi trường, không phụ thuộc vào góc tới và góc khúc xạ → A, C sai

Chiết suất tỉ đối cho biết tia sáng khúc xạ nhiều hay ít khi đi từ môi trường này vào môi trường kia → D đúng

Theo định luật khúc xạ ánh sáng:

Tia khúc xạ nằm trong mặt phẳng tới. → A đúng

Đối với hai môi trường trong suốt nhất định, tỉ số giữa sin của góc tới và sin của góc khúc xạ là một hằng số:

\(\dfrac{{\sin i}}{{\sin r}} = n \to \) C sai

Nếu \(n > 1 \Rightarrow \sin i > \sin r \Rightarrow i > r\)

Nếu \(n < 1 \Rightarrow \sin i < \sin r \Rightarrow i < r \to \) B, D sai

Biểu thức của định luật khúc xạ ánh sáng: \(\dfrac{{\sin i}}{{{\mathop{\rm s}\nolimits} {\rm{inr}}}} = {n_{21}} = \dfrac{{{n_2}}}{{{n_1}}}\)

Căn cứ vào đầu bài ta có: \(\sin i\) tăng hai lần tức là \(\sin {i_2} = 2\sin {i_1}\)

Theo đầu bài, ta có: \(\sin i = n\sin r\)

\( \Rightarrow \left\{ \begin{array}{l}\sin {i_1} = n\sin {r_1}\\\sin {i_2} = n\sin {r_2}\end{array} \right.\)

Ta suy ra: \(\sin {r_2} = \dfrac{{{{{\mathop{\rm sini}\nolimits} }_2}}}{n} = \dfrac{{2\sin {i_1}}}{n} = 2\sin {r_1}\)

=> Khi sin góc tới tăng 2 lần thì sin góc khúc xạ tăng hai lần

A – sai vì tia truyền thẳng không bị đổi hướng

B, C, D - đúng

A, B, C – đúng

D – sai vì: chỉ khi góc tới bằng 0 thì góc khúc xạ mới bằng góc tới và bằng 0

Sin góc tới và sin góc khúc xạ liên hệ với nhau qua biểu thức: \(\sin i = n\sin r\)

A – sai vì: tia truyền thẳng không bị gãy khúc

B – sai vì: tia khúc xạ thuộc mặt phẳng tới và ở bên kia so với pháp tuyến

C – sai vì: góc khúc xạ nhỏ hơn góc tới

D – đúng

Theo định luật khúc xạ ánh sáng:

Ta có:

Tia sáng đi từ không khí vào nước => ứng với việc đi từ môi trường chiết quang kém sang môi trường chiết quang hơn

=> Góc khúc xạ nhỏ hơn góc tới => Tia khúc xạ gần pháp tuyến hơn so với tia tới hay tia khúc xạ xa mặt phân cách giữa hai môi trường hơn so với tia tới

- Theo đầu bài, ta có: độ lớn góc tới và góc khúc xạ bằng \({90^0}\)

\( \Rightarrow i + r = {90^0} = \dfrac{\pi }{2}\)

- Áp dụng định luật khúc xạ ánh sáng:

\(\begin{array}{l}\sin i = n\sin r\\ \Leftrightarrow \sin i = n\sin \left( {\dfrac{\pi }{2} - i} \right) = n\cos i\\ \Rightarrow \tan i = n\end{array}\)

Ta có: chiết suất tuyệt đối của thạch anh:

\(\begin{array}{l}n = \dfrac{c}{v}\\ \Rightarrow v = \dfrac{c}{n} = \dfrac{{{{3.10}^8}}}{{1,55}} = {1,94.10^8}m/s\end{array}\)

Ta có: \({n_1}\sin i = {n_2}\sin r\)

\(\begin{array}{l} \Leftrightarrow 1\sin {40^0} = \dfrac{4}{3}{\mathop{\rm s}\nolimits} {\rm{inr}}\\ \Rightarrow {\mathop{\rm s}\nolimits} {\rm{inr}} = 0,482\\ \Rightarrow r = 28,{82^0}\end{array}\)

Áp dụng định luật khúc xạ ánh sáng ta có:

\(\sin i = n\sin r = \dfrac{4}{3}.\sin 30 = \dfrac{2}{3} \Rightarrow i = {42^0}\)

Theo định luật khúc xạ ánh sáng ta có: \({n_1}\sin 45 = {n_2}\sin 30 \Rightarrow {n_1} < {n_2}\)

→ Môi trường 1 chiết quang kém hơn môi trường 2.

→ Phát biểu sai là: Môi trường 1 chiết quang hơn môi trường 2.

Hướng dẫn giải :

Ta có:

+ \(n = \dfrac{c}{v}\)

+ \(\dfrac{{\sin i}}{{{\mathop{\rm s}\nolimits} {\rm{inr}}}} = n\)

\( \to v = \dfrac{c}{n} = \dfrac{{c{\mathop{\rm s}\nolimits} {\rm{inr}}}}{{\sin i}} = \dfrac{{{{3.10}^8}.\sin {{40}^0}}}{{\sin {{60}^0}}} = 2,{23.10^8}m/s\)

Hướng dẫn giải :

 Từ biểu thức mối liên hệ giữa chiết suất và vận tốc ánh sáng, ta có:

\(n = \frac{c}{v} \to v = \frac{c}{n} = \frac{{{{3.10}^8}}}{{1,6}} = 1,{875.10^8}m/s\)

Áp dụng định luật khúc xạ ánh sáng ta có \(\sin i = n\sin r \Leftrightarrow \sin i = \sqrt 2 .\sin 30 =  > i = {45^0}\)

Áp dụng biểu thức định luật khúc xạ ánh sáng:

n₁sini = n₂sinr => sin45⁰ = n.sin30⁰ => n = \(\sqrt{2}\)